【数据结构与算法分析】02：树（1）

前言： 对于大量的输入数据，链表的线性访问时间太慢，不易使用，提出一种新的数据结构概念——树，下文涉及的数据结构叫做二叉查找树（ binary search tree ）

预备知识： 一棵树是一些节点的集合，该集合可以是空集，若非空，则一棵树由称作根（ root ）的节点r以及0个或多个非空的子树T 1 ，T 2 ，...,T k 组成，每一个子树的根都被来自根r的一条有向的边（ edge ）所连接。

二叉树： （ binary tree ）是一棵树，其中每个节点都不能多于两个的儿子，可以用指针直接指向它们；树节点的声明在结构上类似于双链表的声明，一个节点就是由 Key （关键字）信息加上两个指向其他节点的指针（ left 和 right ）组成的结构。

二叉查找树： 一个节点的左子节点的关键字值小于这个节点，右子节点的关键字值大于或等于这个节点；插入一个节点需要根据这个规则进行插入。

1. 既能像链表那样快速的插入和删除，又能像有序数组那样快速查找；
2. 删除节点是二叉搜索树中最复杂的操作：首先查找要删除的节点，该节点有三种情况：①该节点是叶节点，没有子节点——直接删除；②该节点有一个子节点——在其父节点调整指针绕过该节点后被删除，如图1所示；③该节点有两个子节点——用右子树的最小数据代替该节点的数据并递归的删除那个节点（现在它是空的），如图2所示；
3. 懒惰删除：当一个元素要被删除时，它仍留在树种，而只是做了个被删除的标记；

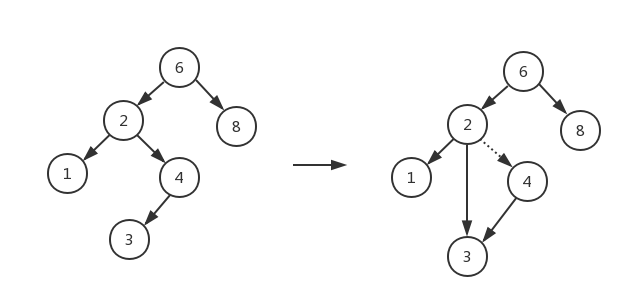
图1 具有一个儿子的节点（4）删除前后的情况

  

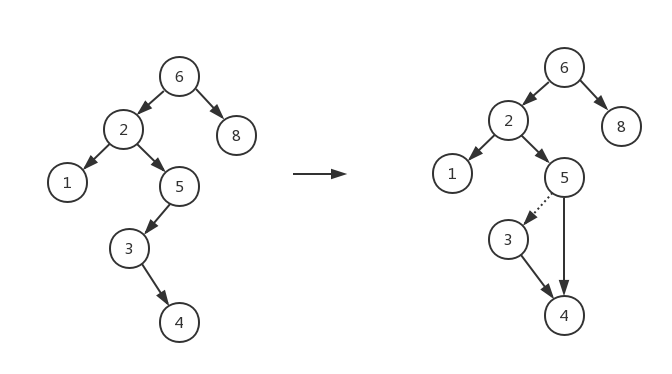
图2 删除具有两个儿子的节点（2）前后的情况

• 若插入的是随机数据，二叉树搜索树执行效果很好，但是如果插入的是有序数据，那么执行速度就会变得很慢，因为插入数值有序时二叉树就是非平衡的排在一条线上，变成了一个链表，其优点能力就丧失了；为了能以较快的时间O(logN)来搜索一棵树，需要保证树总是平衡的（或者至少大部分是平衡的）

AVL树： （ Adelson-Velskii 和 Landis ）树是带有平衡条件的二叉查找树，其每个节点的左子树和右子树的高度最多差1；因此除去可能的插入外，所有的树操作都可以以时间 O(logN)执行。

1. 进行插入操作时，需要更新通向根节点路径上的那些节点的所有平衡信息，该操作隐含困难在于插入一个节点可能破坏AVL树的特性；
2. 通过对树进行简单的修正来恢复平衡，称该修正为旋转；

• 平衡性的修正

不平衡出现的四种情况（把必须重新平衡的节点叫做a）：

1. 对a的左儿子的左子树进行一次插入——LL；
2. 对a的左儿子的右子树进行一次插入——LR；
3. 对a的右儿子的左子树进行一次插入——RL；
4. 对a的右儿子的右子树进行一次插入——RR；

（情况1和4是关于a点的镜像对称，2和3是关于a点的镜像对称，因此理论上只有两种情况）

第一种情况是发生在“外边”的情况（即左-左或右-右），该情况通过对树的一次 单旋转 而完成调整，如图3所示；

第二种情况是插入发生在“内部”的情形（即左-右或右-左），该情况通过单旋转无法修复，通过稍微复杂些的 双旋转 来处理，如图4所示；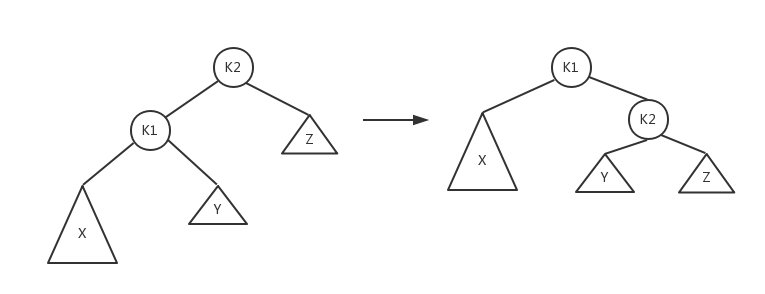

图3 单旋转

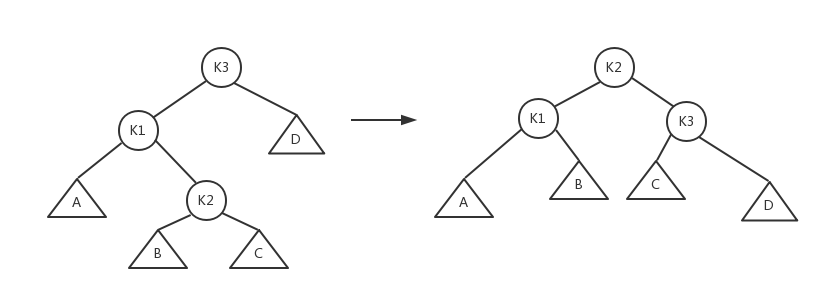
图4 双旋转

AVL树节点类代码：

/**

      * 节点内部类，包括该节点的左右子节点，高度以及节点元素

      */

      private class AvlNode < T extends Comparable < T >> {

            T element ;

            AvlNode < T > left ;

            AvlNode < T > right ;

            int height ; //高度

           

            public AvlNode ( T element ) {

                 this ( element , null , null ) ;

            }

           

            public AvlNode ( T element , AvlNode < T > left , AvlNode < T > right ) {

                 this . element = element ;

                 this . left = left ;

                 this . right = right ;

                 this . height = 0 ;

            }

      }

• LL情况：

/**

      * LL:左左对应的情况（左单旋转）

      *        k2               k1

      *       /  \             /  \

      *      k1   d   ==>     a    k2

      *     /  \             /    /  \

      *    a    c           b    c    d

      *   /

      *  b  

      *  @param AvlNode <T> 不平衡点

      *  @return 旋转后根节点

      */

      private   AvlNode<T>   LL_Rotation ( AvlNode < T > k2 ) {

            AvlNode < T > k1 = k2 . left ;

            k2 . left = k1 . right ;

            k1 . right = k2 ;

           

            k2 . height = max ( Height ( k2 . left ) , Height ( k2 . right )) + 1 ;

            k1 . height = max ( Height ( k1 . left ) , k2 . height ) + 1 ;

           

            return k1;

      }

     

• RR情况：

/**

      * RR:右右对应的情况（右单旋转）

      *        k1               k2

      *       /  \             /  \

      *      d   k2   ==>     k1    c

      *         /  \         /  \    \

      *        a    c       d    a    b

      *              \

      *               b  

      *  @param AvlNode <T> 不平衡点

      *  @return 旋转后根节点

      */

      private AvlNode < T > RR_Rotation ( AvlNode < T > k1 ) {

            AvlNode < T >  k2   = k1 . right ;

            k1 . right =  k2 . left ;

           k2 . left = k1 ;

           

            k1 . height = max ( Height ( k1 . left ) , Height ( k1 . right )) + 1 ;

           k2 . height = max ( Height (k2 . right ) , k1 . height ) + 1 ;

           

            return  k2 ;

      }

• LR情况：

       /**

      * LR:左右对应的情况（左双旋转）

      * 第一次围绕k1进行RR旋转

      * 第二次围绕k3进行LL旋转

      *

      *        k3               k3               k2

      *       /  \    RR       /  \    LL       /  \

      *      k1   d   ==>     k2   d   ==>     k1   k3

      *     /  \             /  \             / \   / \

      *    a    k2          k1    c          a   b c   d

      *         / \        / \

      *        b   c      a   b

      *  @param AvlNode <T> 不平衡点

      *  @return 旋转后根节点

      */

      private AvlNode < T > LR_Rotation ( AvlNode < T > k3 ) {

            k3 . left =  RR_Roatation ( k3 . left ) ;

           

            return LL_Rotation ( k3 ) ;

      }

• RL旋转：

/**

      * RL:右左对应的情况（右双旋转）

      * 第一次围绕k3进行LL旋转

      * 第二次围绕k1进行RR旋转

      * 是与LR对称的情况

      *

      *        k1               k1                  k2

      *       /  \     LL      /  \      RR        /  \

      *      a   k3    ==>    a    k2    ==>     k1   k3

      *         /  \              /  \          / \   / \

      *        k2   d            b    k3       a   b c   d

      *       / \                     / \

      *      b   c                   c   d

      *  @param AvlNode <T> 不平衡点

      *  @return 旋转后根节点

      */

      private AvlNode < T > RL_Rotation ( AvlNode < T > k1 ) {

            k1 . right = LL_Rotation ( k1 . right ) ;

           

            return RR_Rotation ( k1 ) ;

      }

• 插入：

/**

      * 将节点插入到AVL树种，并返回根节点

      * @param tree AVl树的根节点

      * @param element 插入节点的关键字

      * @return 根节点

      */

      public AvlNode < T > Insert ( AvlNode < T > tree , T element ){

            if ( tree == null ) { //树为空

                 //新建节点

                 tree = new AvlNode < T > ( element ) ;  

            } else {

                 //比较大小

                 int cmp = element . compareTo ( tree . element ) ;

                 if ( cmp < 0 ) { //应将节点插入左子树

                      tree . left = Insert ( tree . left , element ) ;

                      //插入节点后， avl 树失去平衡，则就行调整

                      if ( Height ( tree . left ) - Height ( tree . right ) == 2 ) { //第一个左

                            if ( element . compareTo ( tree . left . element ) < 0 ) { //第二个左

                                 //LL情况

                                 tree = LL_Rotation ( tree ) ;

                            } else { //第二个右

                                 //LR情况

                                 tree = LR_Rotation ( tree ) ;

                            }

                      }

                 } else if ( cmp > 0 ) { //应将节点插入右子树

                      tree . right = Insert ( tree . right , element ) ;

                      //插入节点后， avl 树失去平衡，则就行调整

                      if ( Height ( tree . right ) - Height ( tree . left ) == 2 ) { //第一个右

                            if ( element . compareTo ( tree . right . element ) > 0 ) { //第二个右

                                 //RR情况

                                 tree = RR_Rotation ( tree ) ;

                            } else { //第二个左

                                 //RL情况

                                 tree = RL_Rotation ( tree ) ;

                            }

                      }

                 } else { // cmp ==0，相同点，已存在

                      System . out . println ( "ERROR：deny for the same node" ) ;

                 }

            }

           

            tree . height = max ( Height ( tree . left ) , Height ( tree . right )) + 1 ;

           

            return tree ;

      }

     

• 删除：

/**

      * 从树中删除节点

      * @param tree AVL树的根节点

      * @param node 待删除节点

      * @return 根节点

      */

      public AvlNode < T > Remove ( AvlNode < T > tree , AvlNode < T > node ){

            //根为空或没有要删除的节点

            if ( tree == null || node == null ) {

                 return null ;

            }

           

            //比较大小

            int cmp = node . element . compareTo ( tree . element ) ;

            if ( cmp < 0 ) { //向左子树查找

                 tree . left = Remove ( tree . left , node ) ;

                 //删除节点后，进行平衡调整

                 if ( Height ( tree . right ) - Height ( tree . left ) == 2 ) { //第一个右

                      AvlNode < T > right = tree . right ;

                      if ( Height ( right . left ) > Height ( right . right )) { //第二个左

                            //RL情形

                            tree = RL_Rotation ( tree ) ;

                      } else { //第二个右

                            //RR情形

                            tree = RR_Rotation ( tree ) ;

                      }

                 }

            } else if ( cmp > 0 ) { //向右子树查找

                 tree . right = Remove ( tree . right , node ) ;

                 //删除节点后，对树进行平衡

                 if ( Height ( tree . left ) - Height ( tree . right ) == 2 ) { //第一个左

                      AvlNode < T > left = tree . left ;

                      if ( Height ( left . right ) > Height ( left . left )) { //第二个右

                            //LR情形

                            tree = LR_Rotation ( tree ) ;

                      } else { //第二个左

                            //LL情形

                            tree = LL_Rotation ( tree ) ;

                      }

                     

                 }

            } else { //tree是对应的要删除的节点

                 //tree的左右孩子都非空

                 if ( tree . left != null && tree . right != null ) {

                      //如果tree的左子树比右子树高

                      if ( Height ( tree . left ) > Height ( tree . right )) {

                            //1.找出tree左子树中的最大节点

                            AvlNode < T > max = MaxNode ( tree . left ) ;

                            //2.将该最大节点的值赋给tree

                            tree . element = max . element ;

                            //3.删除该最大节点

                            // 这类似于用"tree的左子树中最大节点"做"tree"的替身；

                     // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。

                            tree . left = Remove ( tree . left , max ) ;

                      } else { // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)

                            //1.找出tree右子树的最小节点

                            AvlNode < T > min = MinNode ( tree . left ) ;

                            //2.将该最小节点赋值给tree

                            tree . element = min . element ;

                            //3.删除该最小节点

                            // 这类似于用"tree的右子树中最小节点"做"tree"的替身；

                     // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。

                            tree . right = Remove ( tree . right , min ) ;

                      }

                 } else {

                 AvlNode < T > tmp = tree ;

                 tree = ( tree . left != null ) ? tree . left : tree . right ;

                 tmp = null ;

             }

                

            }

            return tree ;

      }