【八中测试】Constructing Tests

最新推荐文章于 2020-06-26 17:52:48 发布

念JL___初蝶

最新推荐文章于 2020-06-26 17:52:48 发布

阅读量221

点赞数 1

分类专栏： openjudge题库刷题日志

本文链接：https://blog.csdn.net/qq_37862149/article/details/79470022

版权

openjudge题库刷题日志专栏收录该内容

58 篇文章 1 订阅

订阅专栏

这篇博客讨论了如何为一个给定的问题构造测试用例。问题涉及到找到最大的1的数量在m-free矩阵中，矩阵大小为n×n，使得每个m×m的子矩阵至少有一个0。给出t个测试用例，需要找到对应的n和m，使得在这些条件下，1的最大数量等于给定的值xi。解决方案包括理解当0的数量最小时1的数量最大，并建立满足条件的n和m的关系式。

摘要由CSDN通过智能技术生成

B - Constructing Tests

Let’s denote a m-free matrix as a binary (that is, consisting of only 1’s and 0’s) matrix such that every square submatrix of size m × m of this matrix contains at least one zero.

Consider the following problem:

You are given two integers n and m. You have to construct an m-free square matrix of size n × n such that the number of 1’s in this matrix is maximum possible. Print the maximum possible number of 1’s in such matrix.

You don’t have to solve this problem. Instead, you have to construct a few tests for it.

You will be given t numbers x1, x2, …, xt. For every , find two integers ni and mi (ni ≥ mi) such that the answer for the aforementioned problem is exactly xi if we set n = ni and m = mi.

Input

The first line contains one integer t (1 ≤ t ≤ 100) — the number of tests you have to construct.

Then t lines follow, i-th line containing one integer xi (0 ≤ xi ≤ 109).

Note that in hacks you have to set t = 1.

Output

For each test you have to construct, output two positive numbers ni and mi (1 ≤ mi ≤ ni ≤ 109) such that the maximum number of 1’s in a mi-free ni × ni matrix is exactly xi. If there are multiple solutions, you may output any of them; and if this is impossible to construct a test, output a single integer - 1.

Example

Input

Output

5 2
1 1
-1

【解析】

看了Dalao的题解才豁然开朗，原来这道题如此简单：
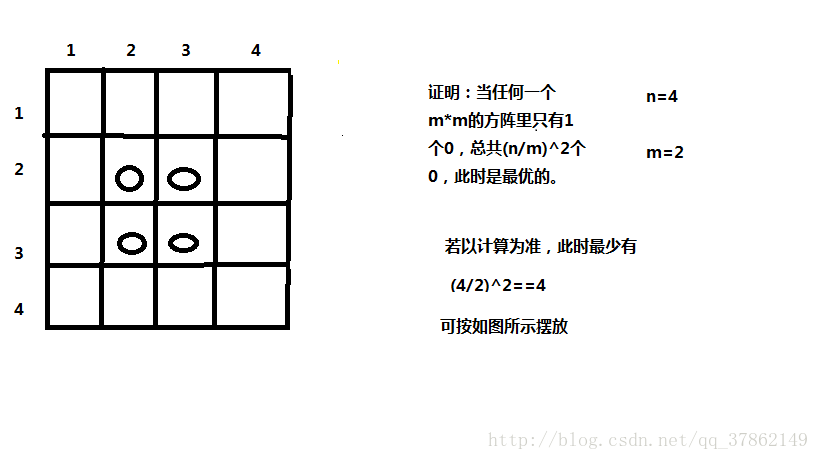
题目要想1的数量最大，则应该0的数量最小，那么何时最小呢？？？任何一个m*m的方阵里只有1个0，总共(n/m)^2个0；0和1的数量一共n*n个因此，应该满足n^2-(n/m)^2==x;即可。
这里写图片描述

AC代码

#include<cstdio>  
#include<cstring>
#include<cmath>
#define MAX 1e5+10  
using namespace std;   
int main(){  
    int T;  
    scanf("%d",&T);  
    while(T--){  
        long long  x;  
        scanf("%lld",&x);  
        if(x==0) printf("1 1\n");  
        else if(x==1) printf("-1\n");  
        else{  
            int flag=0;  
            for(long long  n=1;n<MAX;n++){  
                if(n*n<=x) continue;    
                long long  k=sqrt(n*n-x); //  k=n/m 且不可能为0   
                long long  m=n/k;  
                if(k>0&&n*n-(n/m)*(n/m)==x){  
                    flag=1;  
                    printf("%lld %lld\n",n,m);  
                    break;  
                }     
            }  
            if(!flag) printf("-1\n");  
        }  

    }  
    return 0;  
}