八皇后问题的总结与扩展

八皇后问题是在一个8*8的棋盘内，如何放置8个互不冲突的皇后。我们知道，皇后可以横、直、斜不限距离移动。我们基本上用的是回溯解决此类问题，我这两天看到了不少的八皇后问题解题办法。在我看来，比较高明的解题办法是这种：

public class Queen{
//同列是否有皇后，1表示有
    private int[] column;//右上至左下是否有皇后
    private int[] rup;//左上至右下是否有皇后
    private int[] lup;//解答
    private int[] queen;//解答编号
    private int num;
public Queen(){
    column=new int[8+1];//纵列 共8列 下面的循环式从1开始的 故加1
    rup=new int[(2*8)+1];//右斜纵列 从左上到右下 共有16列
    lup=new int[(2*8)+1];//左斜纵列 从右上到左下 共有16列
for(int i=1;i<=8;i++)
    column[i]=0;
for(int i=1;i<=(2*8);i++)
    rup[i]=lup[i]=0;  //初始定义全部无皇后
    queen=new int[8+1];
}

public void backtrack(int i){//看第i行的皇后在哪里
if(i>8){//当i为9时打印一次
    num++;
    System.out.println("\n解答"+num);

for(int y=1;y<=8;y++){//行
for(int x=1;x<=8;x++){//列
    if(queen[y]==x){//第Y行的皇后在第X列
    System.out.print("Q");
}else{
    System.out.print(".");
}
} 
System.out.println();
}

}else{
for(int j=1;j<=8;j++){
if((column[j]==0)&&(rup[i+j]==0)&&(lup[i-j+8]==0)){//条件合适 在纵列 右斜纵列 左斜纵列 均无棋子
    queen[i]=j;//安排第i行的皇后在第j列
    column[j]=rup[i+j]=lup[i-j+8]=1;
    backtrack(i+1);  //循环调用
    column[j]=rup[i+j]=lup[i-j+8]=0;
}
}
}
}
public static void main(String[]args){
    Queen queen=new Queen();
    queen.backtrack(1);
}
}

它的解题思路是 一排一排的安排棋子 然后列出三个数组 分别代表纵列 右斜纵列 左斜纵列 这样就可以定位一个棋子后确认该棋子控制哪些区域 比如 我们在第一行第一列 布下一个棋子 那么纵列数组column[1]=1 右斜纵列rup[2]=1 左斜纵列lup[8] =1 所以之后的安排棋子就不能选择这三排 至于为什么斜纵列的数组为16

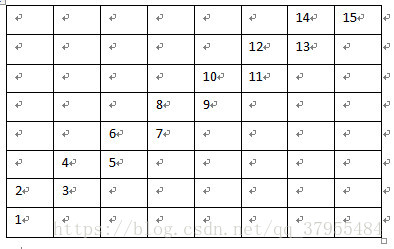
明白了吧 而且数组是从rup[2]开始计算数的（第一行第一列的例子 上一段的内容）
这样顺延下去 答案就出来了

那么 我们为什不做一点扩展的思考呢？如果是七个皇后和一个城堡（横、直不限距离移动）呢?
如果按上面的思路来的话，在确定城堡的位置后它可以控制的位置只有纵列。但是这其实不对 因为有局限性 请看图

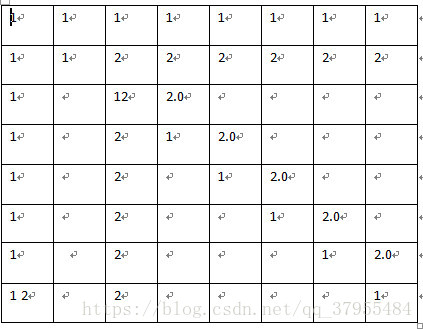
在图中 已经确定了第一个棋子皇后 第二个棋子城堡的位置 它们控制的区域我分别用1 2 来表示 在第三个棋子时 发现了吗？ 如果是在2.0的位置时 第二个皇后就能吃了城堡 这与我们的体意相违背 所以在设定城堡的控制的区域时斜方向也要管 代码如下
`

public class Queen {
    //同栏是否有皇后，1表示有
    private int[] column;
    //右上至左下是否有皇后
    private int[] rup;
    //左上至右下是否有皇后
    private int[] lup;
    //解答
    private int[] queen;
    private int[] castle;//城堡
    //解答编号
    private int num;
    public Queen(){
    column=new int[8+1];
    rup=new int[(2*8)+1];
    lup=new int[(2*8)+1];
    for(int i=1;i<=8;i++)
    column[i]=0;
    for(int i=1;i<=(2*8);i++)
    rup[i]=lup[i]=0;  //初始定义全部无皇后

    queen=new int[8+1];
    castle=new int[8+1];//城堡的数量，没有数据的为零
    }

    public void backtrack(int i, int n){//看第i行的皇后在哪
    int flag = 0;
        for(int q = 1; q<9;q++){
        if(castle[q]!=0)
             flag = 1;
    }
    if(i>8&&flag==1){ //当i为9时打印一次
        num++;
        System.out.println("\n解答"+num);

        for(int y=1;y<=8;y++){//行
        for(int x=1;x<=8;x++){//列
        if(queen[y]==x){ //第Y行的皇后在第X列
            if(castle[y]==x){
            System.out.print("C");  
            }
            else{
        System.out.print("Q");
            }
        }else{
        System.out.print(".");
        }
        }

        System.out.println();
        }
        flag = 0;
    }

    else{
    for(int j=1;j<=8;j++){
    if((column[j]==0)&&(rup[i+j]==0)&&(lup[i-j+8]==0)){
    //条件合适，可以放下棋子
    queen[i]=j;//安排第i行的皇后在第j列 已安排棋子位置
    //设定为占用
    if(n!=0){//可以放城堡
        column[j]=rup[i+j]=lup[i-j+8]=1;
    castle[i]=j;
    n--;
    backtrack(i+1,n);
    column[j]=rup[i+j]=lup[i-j+8]=0;
    castle[i]=0;
    n++;

    }
    column[j]=rup[i+j]=lup[i-j+8]=1;
    backtrack(i +1, n);  //循环调用
    column[j]=rup[i+j]=lup[i-j+8]=0;
    }
    }
    }
    }
    public static void main(String[]args){
    Queen queen=new Queen();
    queen.backtrack(1, 1);//从第一排开始
    }
}

结果是736 也就是92*8 你发现了吗？ 7个皇后已经确认了最后一个棋子的位置了，最后也就只是一个排列组合 换换位置而已 。
谢谢观看！！！