反向传播算法(Backpropagation Algorithm)是一种用于训练多层前馈神经网络的监督学习算法。它通过计算输出层和隐藏层的误差,并利用这些误差调整网络的权重,以最小化整个网络的误差。
首先我们先来看看神经网络的结构:
假设我们有n个输入的标量数据
[
x
1
,
x
2
,
⋯
,
x
n
]
[x_1,x_2,\cdots,x_n]
[x1,x2,⋯,xn],并且我们有m个输出的结果
[
y
1
,
y
2
,
⋯
,
y
m
]
[y_1,y_2,\cdots,y_m]
[y1,y2,⋯,ym],那么我们的神经网络用图像来表示如下:
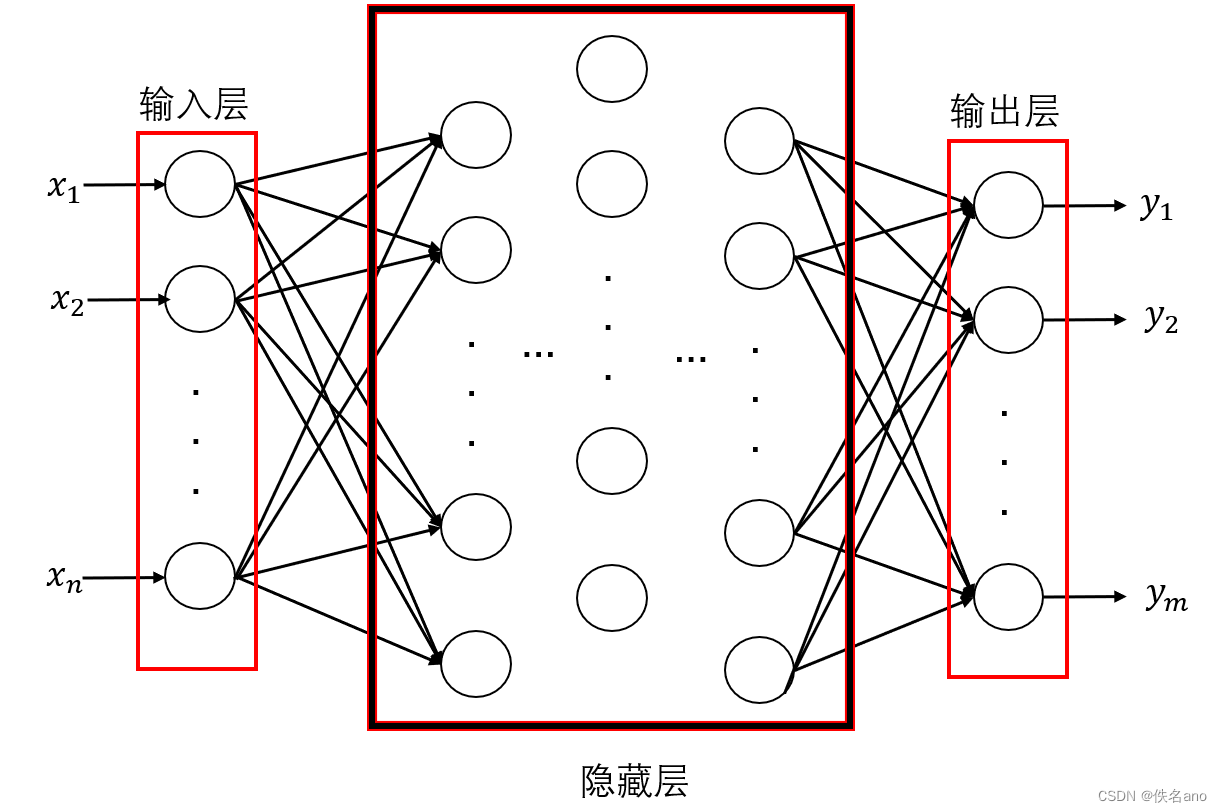
我们输入
[
x
1
,
x
2
,
⋯
,
x
n
]
[x_1,x_2,\cdots,x_n]
[x1,x2,⋯,xn]时,神经网络会在第一层把每一个数据都输入到下一层的每一个节点,就是图上的圆圈,传入的方式就是线性变换,你可以把下一次想象成又一个输入层,不过这次输入的内容是
(
w
i
1
x
1
+
w
i
2
x
2
+
⋯
+
w
i
n
x
n
)
(w_{i_1}x_1+w_{i_2}x_2+\cdots+w_{i_n}x_n)
(wi1x1+wi2x2+⋯+winxn),下一层的节点数也就是输入数我们可以假设为k,那么我们就会有k个向量
[
w
1
1
w
1
2
,
⋯
,
w
1
n
]
,
[
w
2
1
w
2
2
,
⋯
,
w
2
n
]
,
⋯
,
[
w
k
1
w
k
2
,
⋯
,
w
k
n
]
[w_{1_1}w_{1_2},\cdots,w_{1_n}],[w_{2_1}w_{2_2},\cdots,w_{2_n}],\cdots,[w_{k_1}w_{k_2},\cdots,w_{k_n}]
[w11w12,⋯,w1n],[w21w22,⋯,w2n],⋯,[wk1wk2,⋯,wkn]分别代表每一个节点的线性变换系数,以此类推之后的每一对相邻层次的不同节点对直间都有一个这样的权值系数向量,用来和输入值点乘得到标量传入节点.
但是,这样即使参数已经很多了,我们从头到尾对输入参数做的变换都只是线性变换,并没有非线性变换,这里我们就需要再加上一个步骤,那就是非线性变换,我们在每一个节点输入后,把输入的值带入一个函数,得到其非线性变换的输出,这里我们使用的函数有很多种,比如sigmoid函数,relu函数,tanh函数以及他们的变种等等…,这里我们以sigmoid函数为例
sigmoid函数的定义为:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
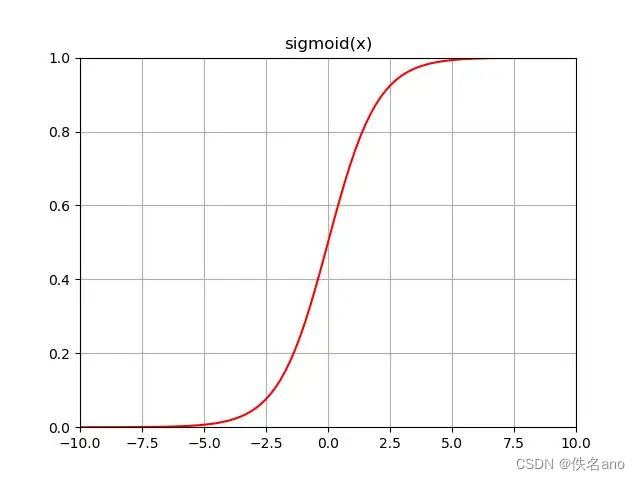
这个函数的图像如下
这个函数图像的特点是范围为[0,1],在0点附近变化速率最快,可以拟合阶跃函数做到平滑过渡,最重要的是,他的导数很好计算
f ( x ) ′ = f ( x ) ( 1 − f ( x ) ) f(x)^{'}=f(x)(1-f(x)) f(x)′=f(x)(1−f(x))
这个等式你可以自己算一算,这样的话这个函数的导数我们就只需要他的输出就可以得到,相当容易
有了sigmoid函数之后我们就可以把输入的值进行线性变换和非线性变换进行输出,并且和期望输出就行比较,神经网络的核心思路就是不断修改网络的权重系数使得这个网络的等价函数可以足够拟合正式情况下的需求,虽然我们可能根本不知道这个需求的函数是什么,但是只要他的输入输出情况能在高概率下和期望的数据相似,那么这个模型就是有效的,我们这里我们要做的就是修改权值.
那么我们该如何修改权重呢?这里我们就可以使用反向传播算法了,我们先定义损失函数
E
(
w
)
=
1
2
∑
d
∈
D
(
t
d
−
o
d
)
2
E(w)=\frac{1}{2}\sum_{d\in D}(t_d-o_d)^2
E(w)=21d∈D∑(td−od)2
- t d 是期望的输出值 t_d是期望的输出值 td是期望的输出值
- o d 是实际的输出值 o_d是实际的输出值 od是实际的输出值
- D 是输出节点集合 D是输出节点集合 D是输出节点集合
这里我们把损失函数定义成输出的均方误差,按照我上面说的,我们训练这个模型的目的就是尽量使模型的输出拟合期望的输出,那么我们的任务就是尽量最小化损失函数,这里涉及最优化的知识,简单来说我们可以使用负梯度下降法得到使损失函数最小的 w w w向量值,接下来我简单聊聊负梯度下降:
这里我们假设一个函数:
h ( x ) = x 1 2 + x 2 2 h(x)=x_1^2+x_2^2 h(x)=x12+x22
如果把他带入代码中绘制出来,或者学习过高等数学的同学们都能看出,这个函数是一个凸函数,在 [ 0 , 0 ] [0,0] [0,0]处最小,好这个时候假设我们并不知道 [ 0 , 0 ] [0,0] [0,0]这个输入的 x x x向量可以使输出最小,为了得到他,我们可以随机找一个初始点比如说 [ 1 , 1 ] [1,1] [1,1],根据偏导的定义,我们可以知道负梯度方向是函数值下降最快的方向,这个时候我们求出这个函数的负梯度向量
− Δ E = − [ ∂ h ( x ) x 1 , ∂ h ( x ) x 2 ] = [ − 2 x 1 , − 2 x 2 ] -\Delta E=-[\frac{\partial h(x)}{x_1},\frac{\partial h(x)}{x_2}]=[-2x_1,-2x_2] −ΔE=−[x1∂h(x),x2∂h(x)]=[−2x1,−2x2]
把[1,1]带入得到[-2,-2],我们得到了函数下降最快的方向,然后要怎么做呢?前进!我们以[-2,-2]为方向,设定一个合适的值为步长前进一步,然后再次计算负梯度再前进,如果步长选取合适,在一定次数的迭代下我们就能走到损失函数变化量足够小的情况也就是达到了最小值点,得到了最优的 x 1 , x 2 x_1,x_2 x1,x2值.
当然了,前提是步长合适,这里我就不绘制例子了,我们想象一下,如果步长过大,可能一下子跨过了最优点,到更远的地方去了,而如果步子过于小,比如说我们设定步长是随迭代次数而不断减小的,可能导致无法迭代到目标点或者耗时过长,又或者恰恰好我们的步长使得我们的取值在最优点左右反复横跳始终无法到最优,所以步长 η \eta η(也叫学习率)的选取也是很有学问的,不过这里不是我们重点讲述的对象.
讲完了负梯度下降方法,大家应该隐约明白了如何优化我们的参数了吧,我们知道,我们定义的损失函数 E E E和我们整个系统的参数都有关系,比如我们想要得到第一层输入层到第二层某对节点的权重最优值使得 E E E最小,我们就要把 E E E对我们要求的权值向量 w w w求负梯度,然后进行迭代优化,这里的 w w w对网络中所有的权重向量都一样,只不过不同位置的向量的负梯度求法可能有所不同,我们以最接近输出的输出层与前一层某对节点直接的权重向量 w w w为例子
要求负梯度:
− ∂ E ∂ w = − ∂ E ∂ o ⋅ ∂ o ∂ x ^ ⋅ ∂ x ^ ∂ w -\frac{\partial E}{\partial w}= -\frac{\partial E}{\partial o}\cdot \frac{\partial o}{\partial \hat x}\cdot \frac{\partial \hat x}{\partial w} −∂w∂E=−∂o∂E⋅∂x^∂o⋅∂w∂x^
这个就是链式法则,其中 o o o就是输出值,所以可以直接通过损失函数的定义求出:
∂ E ∂ o = o d − t d \frac{\partial E}{\partial o}=o_d-t_d ∂o∂E=od−td
而
∂ o ∂ x ^ = p ( x ) ′ \frac{\partial o}{\partial \hat x}=p(x)^{'} ∂x^∂o=p(x)′
这里的定义不就是输出对输入的导数,不就是这节点对应非线性函数的导数吗,还记得我们上面说过我们以sigmoid函数为例吗,所以:
∂ o ∂ x ^ = p ( x ) ′ = p ( x ) ⋅ ( 1 − p ( x ) ) \frac{\partial o}{\partial \hat x}=p(x)^{'}=p(x)\cdot (1-p(x)) ∂x^∂o=p(x)′=p(x)⋅(1−p(x))
而 ∂ x ^ ∂ w \frac{\partial \hat x}{\partial w} ∂w∂x^不就是还没有线性变换的输入值也就是上一层的输出值吗,记作 x x x
完整写下来就是:
− ∂ E ∂ w = − ( o d − t d ) ⋅ p ( x ) ⋅ ( 1 − p ( x ) ) ⋅ x -\frac{\partial E}{\partial w}= -(o_d-t_d) \cdot p(x)\cdot (1-p(x))\cdot x −∂w∂E=−(od−td)⋅p(x)⋅(1−p(x))⋅x
这个公式可以计算输出层的权重,那么隐藏层呢,毕竟最后的公式可是没有解完的,还剩一个 x x x,也就是来自于隐藏层的输出,这里我们取 w w w为某隐藏层直接某对节点之间的权重向量
要求负梯度:
− ∂ E ∂ w = − ∂ E ∂ o ⋅ ∂ o ∂ x ^ ⋅ ∂ x ^ ∂ o ^ ⋯ ∂ x ˜ ∂ w -\frac{\partial E}{\partial w}= -\frac{\partial E}{\partial o}\cdot \frac{\partial o}{\partial \hat x}\cdot \frac{\partial \hat x}{\partial \hat o}\cdots \frac{\partial \~x}{\partial w} −∂w∂E=−∂o∂E⋅∂x^∂o⋅∂o^∂x^⋯∂w∂x˜
可以看出隐层的负梯度求法不过的把链式法则继续加长而言,无非就是不断地嵌套,形式可以写成:
− Δ E ( w ^ ) = − o ^ ⋅ ( 1 − o ^ ) ⋅ Δ E ( w ) ⋅ w ⋅ x -\Delta E(\hat w)=-\hat o\cdot (1-\hat o)\cdot \Delta E(w)\cdot w\cdot x −ΔE(w^)=−o^⋅(1−o^)⋅ΔE(w)⋅w⋅x
其中 w ^ \hat w w^和 w w w对应相邻
而后我们就可以求出 Δ w = − Δ E ⋅ η , w n e w = w + Δ w \Delta w=-\Delta E\cdot \eta,w_{new}=w+\Delta w Δw=−ΔE⋅η,wnew=w+Δw进行权重的更新
这样我们得到了所有权重向量的更新方式,就可以开始编写代码构建我们的神经网络了
好了,以上就是对于反向传播算法的一个简单的介绍,请不吝指正!






















 220
220











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








