数据结构 - 初始化最大、最小堆

1. 堆

堆分为最小堆和最大堆。

• 最小堆：任意一个非叶节点小于其左子树和右子树
• 最大堆：任意一个非叶节点大于其左子树和右子树

2. 初始化堆的步骤

• 首先根据序列构建一个完全二叉树
• （最大堆为例）在完全二叉树的基础上，从最后一个非叶结点开始调整（可理解为从右下角）：比较三个元素的大小–自己，它的左孩子，右孩子。分为三种情况:
  自己最大，不用调整
  左孩子最大，交换该非叶结点与其左孩子的值，并考察以左孩子为根的子树是否满足大顶堆的要求，不满足递归向下处理
  右孩子最大，交换该非叶结点与其右孩子的值，并考察以右孩子为根的子树是否满足大顶堆的要求，不满足递归向下处理

3. 任意序列建立堆

给定任意序列，如：7 8 5 3 9 4

1. 将该序列生成二叉树：
   
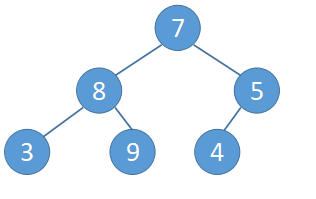
2. 初始化为最小堆：

• 4 < 5 调整
  
• 3 < 8 调整
  
• 3 < 7，4 < 7，3 < 4 调整
  得最小堆序列：3 7 4 8 9 5
  

3. 初始化为最大堆：

• 9 > 8 调整
  
• 9 > 7 调整
  
• 8 > 7 调整
  得最大堆序列：9 8 5 3 7 4
  

4. 在原堆上插入一个值，调整为新的堆

例如，上例中的最大堆为：9 8 5 3 7 4
现插入一个值10，调整为新的最大堆：

• 10 > 5 调整
  
• 10 > 9 调整
  得新的最大堆序列：10 8 9 3 7 4 5
  

最小堆同理。

参考：https://blog.csdn.net/u011240016/article/details/53428489/

完！