代码随想录算法训练营第二十二天 | 491. 非递减子序列、46.全排列、47. 全排列 II、51. N 皇后、37. 解数独

原创已于 2025-11-29 15:46:43 修改 · 1k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

于 2025-11-29 15:36:34 首次发布

代码随想录刷题专栏收录该内容

35 篇文章

订阅专栏

代码随想录算法训练营第二十二天任务

491. 非递减子序列
46. 全排列
47. 全排列 II
332. 重新安排行程（没做出来）（选做）
51. N 皇后（选做）
37. 解数独（选做）

491. 非递减子序列

题目链接：491. 非递减子序列
竟然捣鼓出来了！！！
这道题多少和昨天的题目90. 子集 II 有些像，子集II是有序排除相同的数，这道题是无序排序相同的数。

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int index) {
        if (path.size() >= 2) {
            result.push_back(path);
        }
        for(int i = index; i < nums.size(); ++i) {
            bool flag = false;
            if (i > index) {
                for (int j = index; j < i; ++j) {   // 排除前面出现过的数字。
                    if (nums[j] == nums[i]) flag = true;
                }
            } 
            if (flag) continue;   // 出现过，就跳过。
            if (path.size() == 0 || nums[i] >= path[path.size() - 1]){
                path.push_back(nums[i]);
                backtracking(nums, i + 1);
                path.pop_back();
            }    
        }
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums, 0);
        return result;
    }
};

时间复杂度：O(N * 2^N)
空间复杂度：O(N)

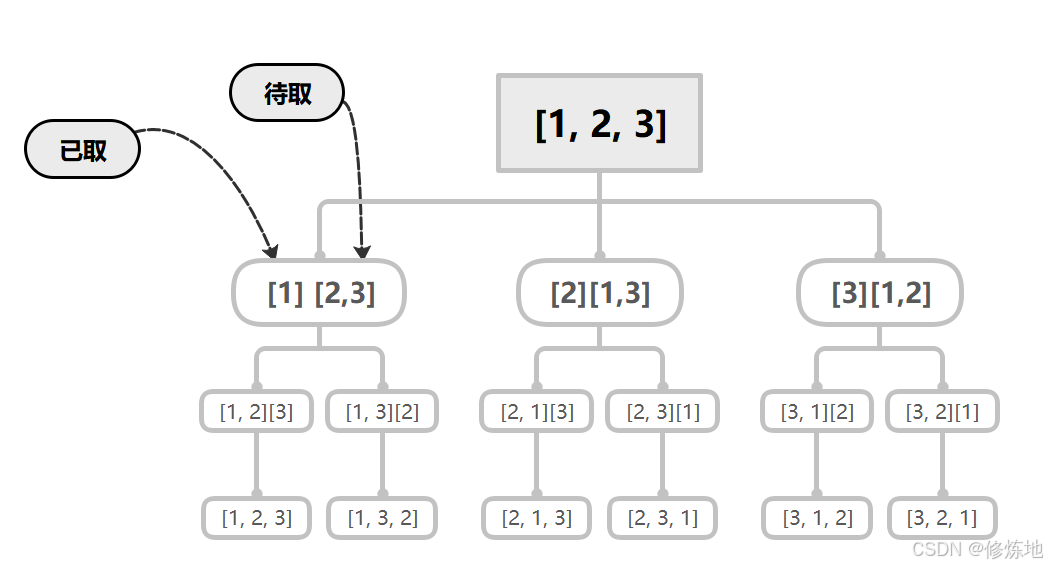
46. 全排列

题目链接：46.全排列
秒过！
思路：同一层从零开始取，但是深度上不能取之前的，用一个used[n]数组标记。
在这里插入图片描述

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, vector<bool> used) {
        if (path.size() == nums.size()) {
            result.push_back(path);
        }
        for (int i = 0; i < nums.size(); ++i) {
            if (!used[i]) {
                path.push_back(nums[i]);
                used[i] = true;
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

时间复杂度：O(N × N!)

排列总数 N!：共有 N! 种排列（N个元素的全排列数）
每条排列的构造代价 O(N)
- 每个排列需要从深度0递归到深度N，每层执行 push/pop 操作
- 具体过程：在递归树的每个节点上，需要遍历 used 数组寻找未使用元素，总体均摊代价为 O(N)
总时间计算
- 对每个排列，生成路径耗时 O(N)
- 总耗时 = N! 个排列 × O(N) = O(N × N!)

空间复杂度：O(N)

递归栈空间：最深 N 层 → O(N)
used 数组：大小为 N → O(N)
path 向量：最多存储 N 个元素 → O(N)
结果集 result：不计入算法辅助空间

47. 全排列 II

题目链接： 47. 全排列 II
横向剔除
之前组合总和II用i>index && nums[i] == nums[i-1] 来剔除同层相同的。没有用used数组来做标记，现在发现用used数组解题更通用，能解组合II也能解排列II。

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, vector<int> used) {
        if(path.size() == nums.size()) {
            result.push_back(path);
        }

        for(int i = 0; i < nums.size(); ++i) {
            if (i > 0 && nums[i] == nums[i-1] && used[i-1] == false) continue;  // 去重
            if (used[i]) continue;
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, used);
            path.pop_back();
            used[i] = false;
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<int> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

时间复杂度分析同上，只不过空间上多了一个used 数组大小 N → O(N)
根据复杂度的运算法则。空间复杂度和上题是一样的。
时间复杂度：O(N * N!)
空间复杂度：O(N)

332. 重新安排行程（没做出来）（选做）

题目链接：332. 重新安排行程
思路：是个全排列问题。可以先对内数组中的字符串排序，再根据一些具体要求剪枝。
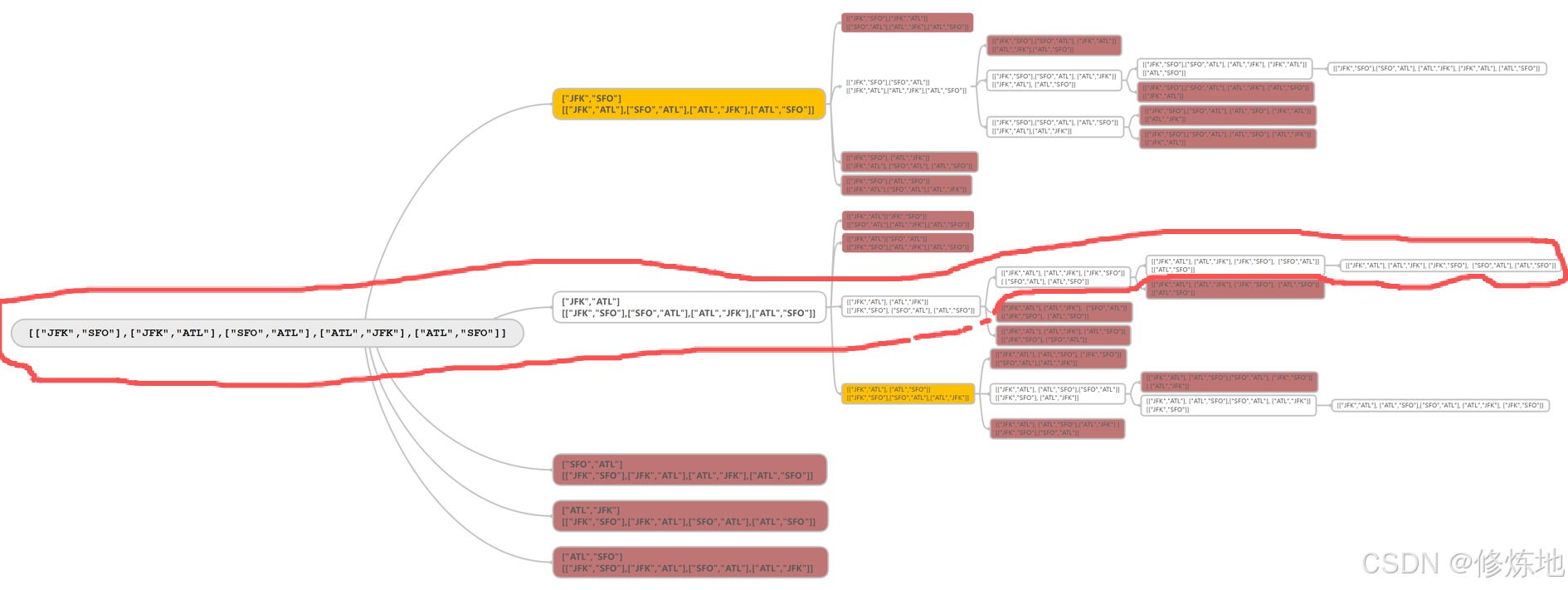
在这里插入图片描述
剪枝不到位？超出时间限制。

class Solution {
private:
    vector<string> res;
    vector<vector<string>> result;
    void backtracking(vector<vector<string>>& tickets, vector<bool> used) {
        // for(auto it : res) {
        //     cout << "“" <<it << "”" ",";
        // }
        // cout << endl;
        if (res.size() == tickets.size() + 1) {
            result.push_back(res);
        }
        for (int i = 0; i < tickets.size(); ++i) {
            if (res.size() == 0 && tickets[i][0] != "JFK") continue;   // 第一个不是“JFK”, 跳过
            if (used[i] == true) continue;  // 已经加入路线的跳过
            if (res.size() > 0 && res[res.size() - 1] != tickets[i][0]) continue;  // 路线不连贯的跳过
            // if (i > 0 && tickets[i][0] == tickets[i-1][0] && used[i-1] == false) continue; // 同层第一个地点相同的。
            if (res.size() == 0) res.push_back(tickets[i][0]);
            res.push_back(tickets[i][1]);
            used[i] = true;
            backtracking(tickets, used);
            res.pop_back();
            if (res.size() == 1) res.pop_back();
            used[i] = false;    
        }
    }
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        sort(tickets.begin(), tickets.end());
        vector<bool> used(tickets.size(), false);
        backtracking(tickets, used);
        return result[0];
    }
};

某一部分票形成环之后，后面的票如何很长的话，回溯的代价太大，容易超时。
太难了，想不出来了。
代码随想录提供的代码也无法通过（力扣修改后台数据，应该不能用回溯了）

51. N 皇后（选做）

题目链接：51. N 皇后
想不出来怎么用回溯解？
看题解
这张图一目了然
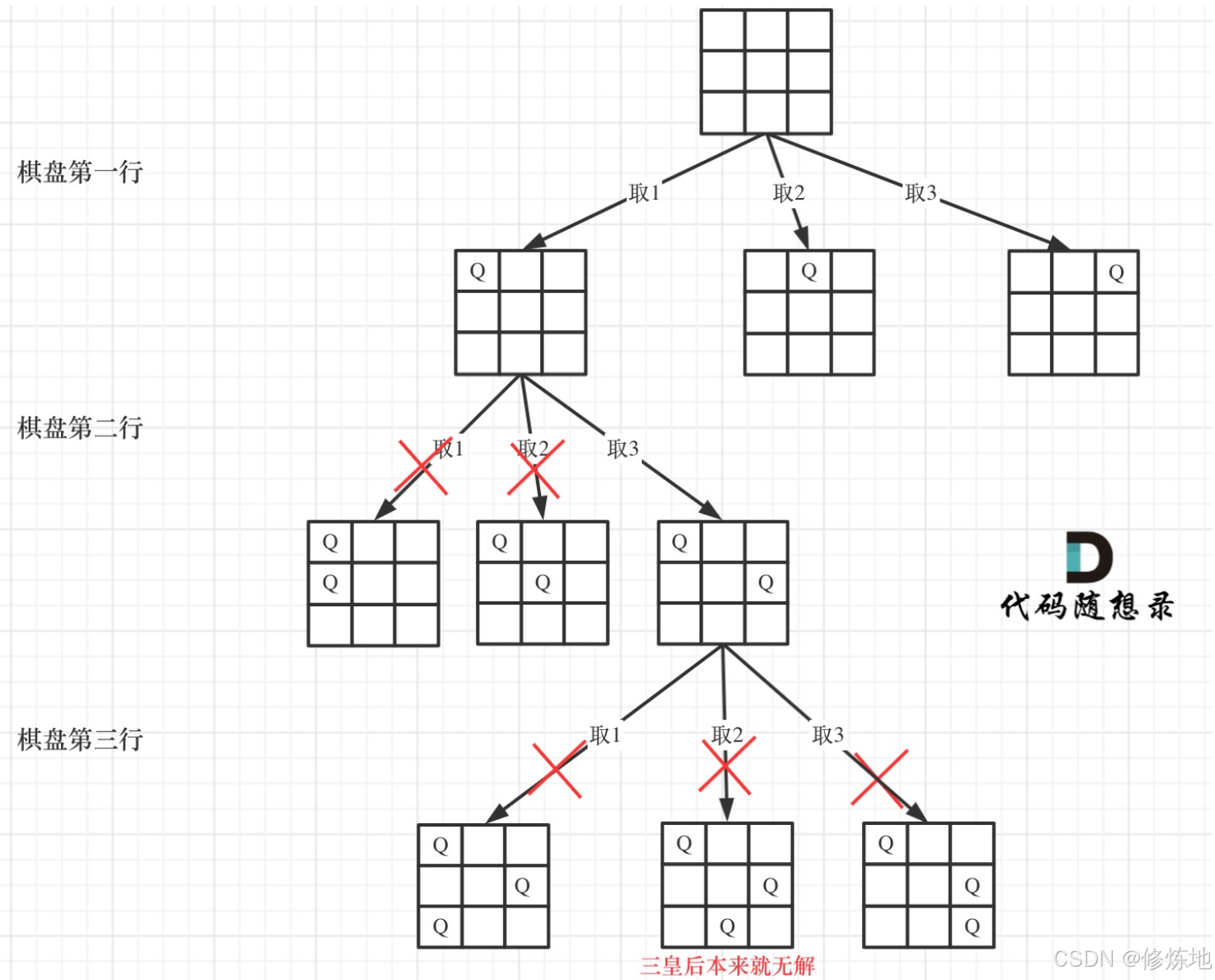
在这里插入图片描述

class Solution {
private:
    vector<vector<string>> result;
    vector<string> chessbord;
    bool isValid(int& row, int& col, int& n) {
        // 检查列
        for (int i = 0; i < row; ++i) {
            if (chessbord[i][col] == 'Q') return false;
        }
        // 检查45°
        for (int i = row-1, j = col+1; i>=0 && j<n; --i, ++j) {
            if(chessbord[i][j] == 'Q') return false;
        }
        // 检查135°
        for (int i = row-1, j = col-1; i>=0 && j>=0; --i, --j) {
            if (chessbord[i][j] == 'Q') return false;
        }
        return true;
    }
    void backtracking(int& n, int row) {
        if (row == n) {
            result.push_back(chessbord);
            return;
        }
        for(int i = 0; i < n; ++i) {  // 遍历列
            if(isValid(row, i, n)) {
                chessbord[row][i] = 'Q';
                backtracking(n, row + 1);  // 递归行
                chessbord[row][i] = '.';
            }
        }
    }
public:
    vector<vector<string>> solveNQueens(int n) {
        chessbord = vector<string>(n, string(n, '.'));
        backtracking(n, 0);
        return result;
    }
};

时间复杂度： O(N × N!) 搜索树规模 N!，每层验证 O(N)
空间复杂度： O(N²) 棋盘占用 N²，递归栈 N

37. 解数独（选做）

题目链接： 37. 解数独
思路：对每个单元格进行递归

class Solution {
private:
    bool isValid(vector<vector<char>>& board, int row, int col, char data) {
        // 检查行
        for (int i = 0; i < 9; ++i) {
            if (board[row][i] == data) return false;
        }
        // 检查列
        for (int i = 0; i < 9; ++i) {
            if (board[i][col] == data) return false;
        }
        // 检查所在的3x3宫格
        for (int i = row/3 * 3; i < (row/3 + 1) * 3; ++i) {
            for (int j = col/3 * 3; j < (col/3 + 1) * 3; ++j) {
                if (board[i][j] == data) return false;
            }
        }
        return true;
    }
    bool backtracking(vector<vector<char>>& board, int row, int col) {
        if (row == 9) return true;  // 找到解
        if (col == 9) return backtracking(board, row + 1, 0);  // 换行
        if (board[row][col] != '.') return backtracking(board, row, col + 1); // 跳过已填充
        for (char data = '1'; data <= '9'; ++data) {
            if (isValid(board, row, col, data)) {
                board[row][col] = data;
                if (backtracking(board, row, col + 1)) return true;
                board[row][col] = '.';  // 回溯
            }
        }
        return false;   // 无解，回溯
    }
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board, 0, 0);
    }
};

时间复杂度：O(9^N×N) N是空格数，最坏指数级
空间复杂度：O(N²) 棋盘N² + 递归栈N

回溯总结：
组合问题：N个数里面按一定规则找出k个数的集合（startIndex来控制for循环的起始位置）
排列问题：N个数按一定规则全排列，有几种排列方式（不用使用startIndex）
切割问题：一个字符串按一定规则有几种切割方式（抽象为一个回溯问题）
子集问题：一个N个数的集合里有多少符合条件的子集（不需要终止条件）
棋盘问题：N皇后，解数独等等（抽象为一个回溯问题）
注意：数组中有重复的数字，而结果不能重复的ji