《特征值与特征向量》定义、意义及例子

1.特征值和特征向量的定义

2.例子

3.特征值和特征向量的几何意义

对于上面的例子，我们求得的特征值和特征向量，例如：对于特征值$\lambda =2$，特征向量$x=[2,-1{]}^T$有：

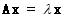
可以看出向量x经过矩阵A变换后，等价于向量x拉伸$\lambda$倍，其方向并未改变。

因此将特征向量看成基向量，矩阵就是这些基向量向对应的特征值伸展所需的数学运算。给定一个矩阵，就可以找出对应的基（特征向量），及透过向量变换（矩阵），这些基的伸展（特征值）。

参考：
特征值与特征向量
线性代数：如何求特征值和特征向量