浅析信号与系统1（指数信号与正弦信号）

本文链接：https://blog.csdn.net/qq_38890412/article/details/117258006

1. 连续时间信号与离散时间信号

1. 连续时间信号与离散时间信号

连续时间信号：自变量是连续可变的，因此信号在自变量的连续值上都有定义

离散时间信号：定义在离散时刻点上。

2. 自变量的变换

首先，时移是一种简单且很重要的信号自变量变换。在离散时间情况下的时移如下图所示：

这里有两个信号 $x[n]$ 和 $x[n-n_0]$ ，它们在形状上是完全一样的，但在位置上互相有个移位。在连续时间情况遇到的时移如下图所示，这里 $x(t-t_0)$ 代表一个延时( $t_0$ 为正)的 $x(t)$ ，或是一个超前( $t_0$ 为负)的 $x(t)$ 。这种形式关联的信号可以在声纳、地震信号处理以及雷达等应用中找到。

时间轴的第二种基本变换是 时间反转。例如 $x[-n]$ 就是将 $x[n]$ 以 n=0 为轴反转得到的。

第三种基本变换是时间尺度变换（time scaling）。如果把 $x(t)$ 想象为一盘录音磁带的话，那么 $x(2t)$ 将是这盘磁带以两倍的速度放音的结果，而 $x(t/2)$ 则代表原磁带将放音速度降低一半。

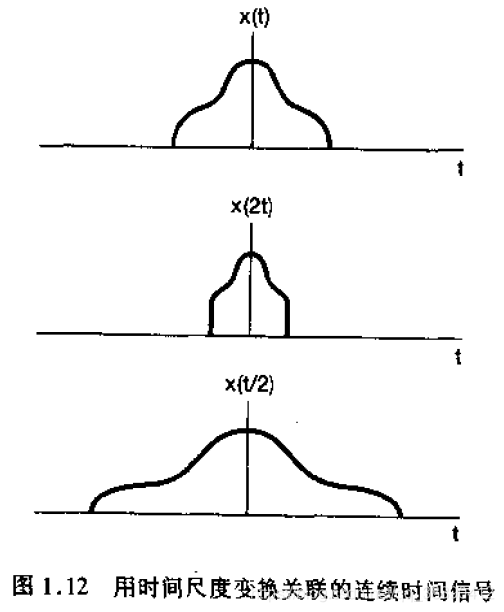
以上各种变化都可以结合到一起，例如

时移+反转变换： $x(-t + 1)$

时移+尺度变换： $x(\frac{3}{2}t + 1)$

尺度+反转变换： $x(-\frac{3}{2}t)$

3. 周期信号

一个周期的连续信号 $x(t)$ 具有这样的性质，即存在一个正值的T，对全部t来说，有 $x(t)=x(t+T)$ ，即当一个周期信号时移T后其值不变。这时就说 $x(t)$ 是一个周期信号，周期为T。

如果 $x(t)$ 是周期的，周期为T，那么对全部 t 和任意 m 来说就有 $x(t)=x(t+mT)$ ，由此 $x(t)$ 对于周期 2T, 3T, 4T, … 等等都是周期的。对于使 $x(t)=x(t+T)$ 成立的最小正值 T 称为 $x(t)$ 的基波周期 $T_0$ 。

在离散时间下可类似地定义出周期信号，即如果一个离散时间信号 $x[n]$ 时移一个N后其值不变，即对全部n值有 $x[n] = x[n + N]$ ，其基波周期 $N_0$ 为最小正值N。

4. 偶信号与奇信号

偶： $x(-t) = x(t)$

奇： $x(-t) = -x(t)$ ， $x(0) = 0$

任何信号都能分解成两个信号之和，其中之一为偶信号，另一个为奇信号

5. 指数信号与正弦信号

连续时间复指数信号具有如下形式： $x(t) =Ce^{at}$ 。式中的C和a一般为复数。根据这些参数值的不同，复指数信号可有几种不同的特征。

实指数信号

$x(t) =Ce^{at}$ ，若 C 和 a都是实数（这时 $x(t)$ 就称为实指数信号），就有两种类型的特性，若a为正实数，那么 $x(t)$ 随t的增加而指数增长（比如描述原子爆炸）。若a是负实数，则 $x(t)$ 随 t 的增加而指数衰减。这类幸好可用来描述放射性衰减、RC电路以及有阻尼的机械系统的相应等范围广泛的各种现象。

周期复指数和正弦信号

第二种重要的复指数信号是将a限制为纯虚数，特别是考虑如下信号： $x(t) =e^{iw_0t}$ ，该信号的一个重要性质在于它是周期信号。为证明这一点，可根据 $x(t)=x(t+T)$ ，如果存在一个T使下式成立： $e^{iw_0t} = e^{iw_0(t+T)}$ ，则 $x(t)$ 就是周期的。为此 $e^{iw_0(t+T)} = e^{iw_0t} e^{iw_0T}$ ，必须有 $e^{iw_0T}$ = 1，若 $w_0$ = 0， $x(t) = 1$ ，这时对任何T值都是周期的；若 $w_0$ ≠ 0，那么使 $e^{iw_0T}$ = 1 成立的最小正T值，即基波周期 $T_0$ 应为 $T_0 = \frac{2 \pi}{\left |w_0 \right |}$ ，可见 $e^{iw_0t}$ 和 $e^{-iw_0t}$ 都是具有同一基波周期的周期信号。

和周期复指数信号密切相关的一种信号是正弦信号。

$x(t) = Acos(w_0t+\phi)$

用秒做t的单位，则 $\phi$ 的单位就是弧度，而 $w_0$ 的单位就是 rad/s。一般又可写成 $w_0 = 2 \pi f_0$ ， $f_0$ 的单位是周期数/秒，即Hz。利用欧拉(Euler)关系，复指数信号可以用其相同基波周期的正弦信号来表示，即 $e^{iw_0t} = cosw_0t + jsinw_0t$

同样，正弦信号 $x(t) = Acos(w_0t+\phi)$ 也能用相同基波周期的复指数信号来表示，即 $Acos(w_0t+\phi) = \frac{A}{2}e^{i\phi}e^{iw_0t} + \frac{A}{2}e^{-j\phi}e^{-jw_0t}$ ，注意，本式的两个指数信号都有复数振幅，所以正弦信号还可以用复指数信号表示为如下形式： $Acos(w_0t+\phi) = A\delta\left \{ e^{j(w_0t + \phi)} \right \}$

由 $T_0 = \frac{2 \pi}{\left |w_0 \right |}$ 得，连续时间正弦信号或一个周期复指数信号其基波周期 $T_0$ 是与 $\left | w_0 \right |$ （ $\left | w_0 \right |$ 又称基波频率）成反比的，也就是说如果 $\left | w_0 \right |$ 减小，就减慢了 $x(t)$ 的振荡速率，因此周期增长。现在考虑 $\left | w_0 \right |$ =0 的情况，正如早先已经指出的，这时 $x(t)$ 为一常数，因此对于任意正值T它都是周期的，所以常数信号的基波周期无定义。另一方面，在这种情况下若定义一个常数信号的基波频率为零，也就是说振荡速率为零，这也不会引起什么混淆。

周期复指数信号在讨论信号与系统的大部分问题中都起着非常重要的作用，部分原因是由于对其它信号来说，它们可用作极其有用的信号基本构造单元。同时，一组成谐波关系的复指数信号也是很有用的；也就是周期复指数信号的集合，该集合内的全部信号都是周期的，且有一个公共周期 $T_0$ 。对一个复指数信号 $e^{iwt}$ 要成为具有周期为 $T_0$ 的周期信号的必要条件是： $e^{iwT_0} = 1$ 。这就意味着 $wT_0$ 是 2π的倍数，即 $wT_0 = 2\pi k, k=0, \pm 1, \pm 2, ...$ ，由此，若定义 $w_0 = \frac{2\pi}{T_0}$ ，可以得出为满足 $wT_0 = 2\pi k, k=0, \pm 1, \pm 2, ...$ ，w必须是 $w_0$ 的整倍数。这就是说，一个成谐波关系的复指数信号的集合就是一组其基波频率是某一正频率 $w_0$ 的整数倍的周期复指数信号，即 $\phi_k(t) = e^{ikw_0t}, k=0, \pm1, \pm2, ...$ ，若 k=0， $\phi_k(t)$ 就是一个常数；而对任何其它的k值， $\phi_k(t)$ 是周期的，其基波频率为 $\left | k \right |w_0$ ，基波周期为 $\frac{2\pi}{\left | k \right |w_0} = \frac{T_0}{\left | k \right |}$ 。因为在任何长度为 $T_0$ 的时间间隔内，恰好通过了 $\left | k \right |$ 个基波周期，所以第k次谐波 $\phi_k(t)$ 对 $T_0$ 来说仍然是周期的。

例

有时希望把两个复指数的和化成单一的复指数和单一的正弦函数的乘积来表示。例如我们要想画出下面信号的模 $x(t) = e^{i2t} + e^{i3t}$ ，为此可以首先将上式右边的两个复指数进行因式分解，其具体作法是将右边和式的两个指数中的频率求得它们的平均值，然后作为公共因子提出来，为此可得 $x(t) = e^{i2.5t}(e^{-i0.5t} + e^{i0.5t})$ ，根据欧拉关系，上式可写成 $x(t) = 2e^{i2.5t}cos(0.5t)$ ，从上式就可以直接得出 $x(t)$ 的模的表达式为 $\left | x(t) \right | = 2 \left |cos(0.5t) \right |$ 。在这里已经用到复指数 $e^{i2.5t}$ 的模总是1这一点。 $\left | x(t) \right |$ 就是一般的全波整流过的正弦波，如下图所示：

一般复指数信号

最一般情况下的复指数信号可以借助于已经讨论过的实指数信号和周期复指数信号来给予表示和说明。考虑某一复指数信号 $Ce^{at}$ ，将 C用极坐标，a用直角坐标表示，分别有 $C = \left | C \right | e^{i \theta}$ 和 $a = r + jw_0$ ，那么 $Ce^{at} = \left | C \right |e^{i\theta}e^{(r+jw_0)t} = \left | C \right | e^{rt}e^{j(w_0t+\theta)}$ 。