网络流:最大流与最小割
想象一下城市中的供水系统:水源是水库,终点是居民区,中间的管道有不同容量限制。如何让最多的水从水库流向居民区?这就是最大流问题。而最小割则像是找出最经济的管道切断方案,使水库和居民区完全断开。今天我们就来探讨这两个密切相关的网络流问题。
一、网络流基础概念
让我们先理解一些基本概念,就像学习交通规则前要先认识道路标志一样。
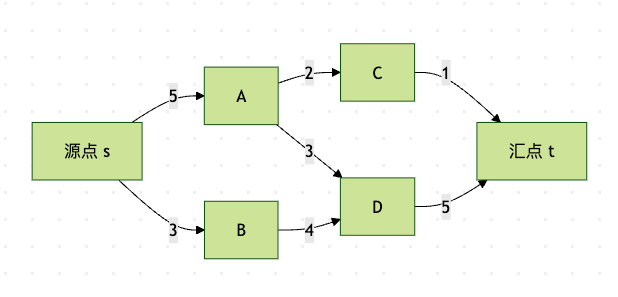
以上流程图展示了一个简单的网络流示例,其中s是源点,t是汇点,其他节点是中间节点,边上的数字表示容量。
在网络流理论中,我们通常用有向图G=(V,E)表示网络,其中:
- V是顶点集,包含源点s和汇点t
- E是边集,每条边(u,v)∈E有一个非负容量c(u,v)≥0
- 如果(u,v)∉E,则c(u,v)=0
1.1 流的基本性质
一个流f是从V×V到实数集的函数,满足以下性质:
- 容量限制:对于所有u,v∈V,0 ≤ f(u,v) ≤ c(u,v)
- 反对称性:对于所有u,v∈V,f(u,v) = -f(v,u)
- 流量守恒:对于所有u∈V-{s,t},∑f(u,v)=0 (v∈V)
理解了这些基本概念后,我们来看最大流问题的定义。
二、最大流问题
最大流问题的目标是找到从源点s到汇点t的最大流量。就像我们想最大化供水系统中的水流量一样。
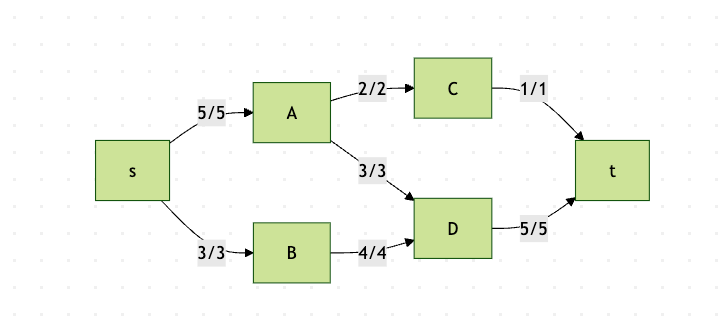
这个流程图展示了最大流的一个解,边上的x/y表示流量x和容量y,总流量为6。
2.1 Ford-Fulkerson方法
Ford-Fulkerson是解决最大流问题的经典方法,其核心思想是不断寻找增广路径。
// Ford-Fulkerson算法伪代码
1. 初始化流f为0
2. while (存在从s到t的增广路径p) {
3. 沿着p增加流f
4. }
5. return f
上述代码说明了Ford-Fulkerson算法的基本框架,关键在于如何寻找增广路径。
2.1.1 残量网络
残量网络G_f由可以容纳更多流的边组成。对于G中的每条边(u,v),在G_f中:
- 如果f(u,v) < c(u,v),则有一条边(u,v)∈G_f,容量为c_f(u,v)=c(u,v)-f(u,v)
- 如果f(u,v) > 0,则有一条边(v,u)∈G_f,容量为c_f(v,u)=f(u,v)
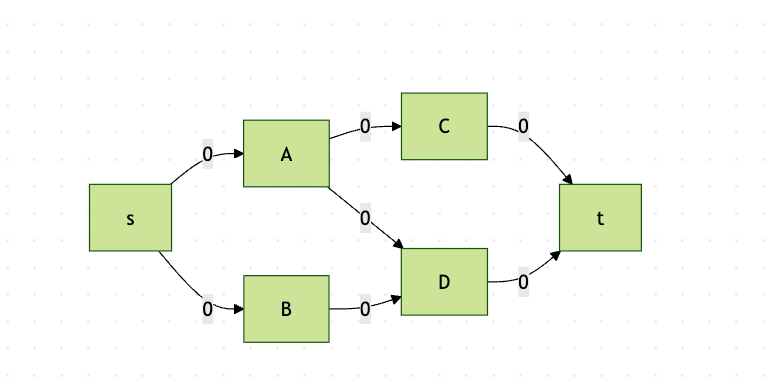
这是初始残量网络,与原网络相同,因为初始流量为0。
2.2 Edmonds-Karp算法
Edmonds-Karp是Ford-Fulkerson的具体实现,使用BFS寻找增广路径,保证多项式时间复杂度O(VE²)。
// Edmonds-Karp算法实现示例
def edmonds_karp(C, s, t):
n = len(C)
F = [[0] * n for _ in range(n)]
while True:
# BFS寻找增广路径
parent = [-1] * n
parent[s] = -2
queue = [s]
found = False
while queue and not found:
u = queue.pop(0)
for v in range(n):
if parent[v] == -1 and C[u][v] - F[u][v] > 0:
parent[v] = u
if v == t:
found = True
break
queue.append(v)
if not found:
break
# 计算路径上的最小残量
path_flow = float('inf')
v = t
while v != s:
u = parent[v]
path_flow = min(path_flow, C[u][v] - F[u][v])
v = u
# 更新流量
v = t
while v != s:
u = parent[v]
F[u][v] += path_flow
F[v][u] -= path_flow
v = u
return sum(F[s][i] for i in range(n))
这段Python代码实现了Edmonds-Karp算法,使用BFS寻找增广路径,确保算法效率。
三、最小割问题
理解了最大流后,我们来看与之对偶的最小割问题。就像找到最经济的管道切断方案。
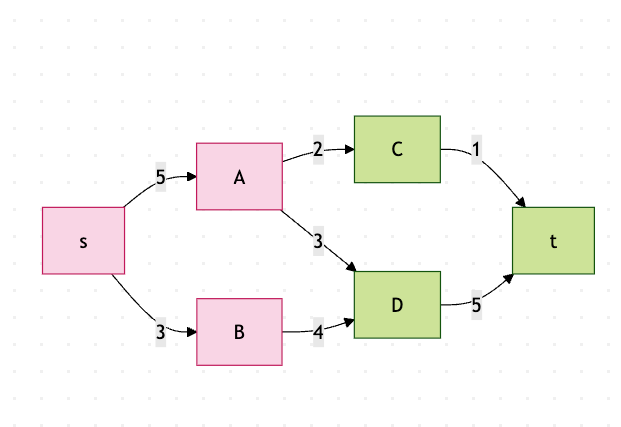
这个图中粉色区域表示一个割(S,T),其中S={s,A,B},T={C,D,t}。割的容量是c(A,C)+c(A,D)+c(B,D)=2+3+4=9。
3.1 最大流最小割定理
这个定理揭示了最大流和最小割之间的深刻联系:
最大流最小割定理:在任何流网络中,从s到t的最大流的值等于最小s-t割的容量。
这个定理告诉我们,网络的最大传输能力受限于最窄的"瓶颈"。就像水管系统的最大流量受限于最细的管道一样。
3.2 如何找到最小割
在Edmonds-Karp算法结束后,我们可以通过残量网络找到最小割:
def find_min_cut(C, F, s):
n = len(C)
visited = [False] * n
queue = [s]
visited[s] = True
while queue:
u = queue.pop(0)
for v in range(n):
if not visited[v] and C[u][v] - F[u][v] > 0:
visited[v] = True
queue.append(v)
S = [i for i in range(n) if visited[i]]
T = [i for i in range(n) if not visited[i]]
return S, T
这段代码展示了如何在计算最大流后找到最小割,通过BFS在残量网络中找出从s可达的节点。
四、应用实例
让我们通过一个实际例子来巩固理解。考虑以下网络:
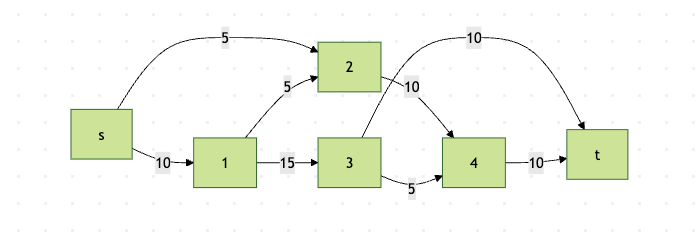
这个网络流问题的最大流可以通过Edmonds-Karp算法求解,最小割可以通过最大流最小割定理找到。
4.1 求解步骤
- 初始化所有流量为0
- 找到第一条增广路径s→1→3→t,增加流量10
- 找到第二条增广路径s→2→4→t,增加流量5
- 找到第三条增广路径s→1→2→4→t,增加流量5
- 无法找到更多增广路径,算法终止
最终最大流为20,最小割为{(1,3), (2,4), (4,t)},容量也是20,验证了最大流最小割定理。
五、总结
通过今天的讨论,我们深入理解了网络流中的两个核心问题:
- 最大流问题:寻找从源点到汇点的最大流量
- 最小割问题:寻找使源汇点分离的最小容量边集
- 最大流最小割定理:这两个问题的解在数值上相等
- 解决方法:Ford-Fulkerson方法及其具体实现Edmonds-Karp算法
网络流算法在实际中有广泛应用,如交通规划、电力分配、网络带宽管理等。希望这篇文章能帮助大家理解这些重要概念,并在实际问题中加以应用。
文章目录结构总结:
-
网络流基础概念
-
最大流问题
- Ford-Fulkerson方法
- Edmonds-Karp算法
-
最小割问题
- 最大流最小割定理
- 如何找到最小割
-
应用实例
-
总结






















 4359
4359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








