Leetcode48题：旋转图像

1.题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/rotate-image

2.思路分析

用翻转操作代替旋转操作。如下所示：

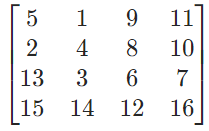
 作为例子，先将其通过水平轴翻转得到：

 再根据主对角线翻转得到：

 就得到了答案。这是为什么呢？对于水平轴翻转而言，我们只需要枚举矩阵上半部分的元素，和下半部分的元素进行交换，即

 对于主对角线翻转而言，我们只需要枚举对角线左侧的元素，和右侧的元素进行交换，即

 将它们联立即可得到：

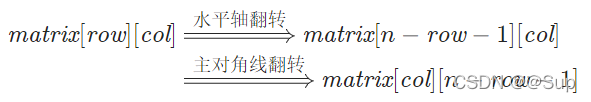
 3.解答

class Solution {
    //水平翻转 + 主对角线翻转

    public void rotate(int[][] matrix) {
        int n = matrix.length;

        //1.先水平翻转
        for(int i = 0; i < n / 2; i++){
            for(int j = 0; j < n; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }

        //2.再沿主对角线翻转
        for(int i = 0; i < n; i++){
            for(int j = 0; j < i; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

时间复杂度：O(N^2)，其中 N 是 matrix 的边长。对于每一次翻转操作，我们都需要枚举矩阵中一半的元素。

空间复杂度：O(1)。为原地翻转得到的原地旋转。