蛇形/回形矩阵（超详细！看了不会你来打我）

回型矩阵

给你一个整数n，按要求输出n∗n的回型矩阵
例如输入n=4，输出如下：

分析

回形矩阵的填充轨迹如下所示：

填充顺序：

最上面的行——>最右边的列——>最下面的行——>最左边的列——>最上面的行——>……

首先，我们可以看出，填充轨迹存在大小不等的回形，我称之为外回与内回。

如何控制外回结束后，会进入内回？

需要4个变量作为边界限制条件，随着外回的进行，不断缩紧边界限制条件，逐步迫使轨迹进入内回。具体设置如下所示：

设置了这4个限制条件还不够哦！因为这4个条件只会限制回的轨迹，但并不适合用来控制数字的写入！为什么这么说？看：

假设现在利用边界限制条件去控制数字写入：
第一行的写入过程如下：

现在需要输入最右边的列，top很明显需要更新，假设我们更新了top

接下来输入最右边的列：

那么现在问题来了！

按理说，当top==bottom并且left==right时，矩阵应该已经被填充完成，而此时我们竟然只填充了6个格子！还没开始就结束了！令人猝不及防。

就算我们之后可以通过什么神奇的方法将4个条件恢复，必然也会导致复杂的逻辑，划不来！

上面大概解释了4个边界条件不能用来控制数字写入的原因，接下来就谈谈正确的解答姿势！

我们再引入4个变量l,r,b,t去控制数字的写入！

先是最上面的行，令l=left,而后在l<=right的条件下，++l一直执行，同时输入数字。当最后一个数字填入时，我们令++top,上界下移。

然后是最右边面的列，令t=top,而后在t<=bottom的条件下，++t一直执行，同时输入数字。当最后一个数字填入时，我们令--right,右界左移。

然后是最下面的行，令r=right,而后在r>=left的条件下，--r一直执行，同时输入数字。当最后一个数字填入时，我们令--bottom,下界上移。

然后是最左边的列，令b=bottom,而后在b>=top的条件下，--b一直执行，同时输入数字。当最后一个数字填入时，我们令++left,左界右移。

现在就剩下一个2*2的矩阵了，和上面一样的执行流程，既然是一样的，那么逻辑相同，循环解决！

code

上面解释的挺详细了，代码就不注释了

#include <iostream>
#include <vector>
using namespace std;
class Solutions{
public:
    void ShowMatrix(const vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j)
                printf("%4d ", matrix[i][j]);
            cout << endl;
        }
    }
    vector<vector<int>> Clip(const int& n) {
        vector<vector<int>> clip(n, vector<int>(n));
        int left = 0, top = 0, right = n - 1, bottom = n - 1;
        int l, r, b, t;
        int num = 1;
        while (num <= n * n) {//循环条件可换top==bottom && left==right
            l = left;
            while (l <= right)
                clip[top][l++] = num++;
            ++top;
            t = top;
            while (t <= bottom)
                clip[t++][right] = num++;
            --right;
            r = right;
            while (r >= left)
                clip[bottom][r--] = num++;
            --bottom;
            b = bottom;
            while (b >= top)
                clip[b--][left] = num++;
            ++left;
        }
        return clip;
    }
};
int main() {
    int n;
    cin >> n;
    Solutions s;
    vector<vector<int>> m(n, vector<int>(n));
    m = s.Clip(n);
    s.ShowMatrix(m);
    return 0;
}

【注】：代码并没有对异常输入进行控制！不可输入负数！

效果

蛇形矩阵

给你一个整数n，输出n∗n的蛇形矩阵。
例如输入n=4，输出如下：

分析

蛇形矩阵的填充轨迹如下所示：

填充规律：

斜向上——>斜向下——>斜向上——>……

如何控制斜向上/下

边界的控制不可避免，如下图所示，格子中的箭头表示这个字是在哪个方向被填充数字的,还有一圈虚线画出的格子，称之为虚界。

虚界在矩阵中并不存在，但当矩阵的索引进入虚界，说明索引非法！

但换个角度想，一旦索引进入虚界，说明正在填充方向的格子已经全部填充，需要换方向了！

所以说虚界的意义在于控制方向的转换！如回型矩阵中的4个边界条件一般。

由上图可以轻松看出，两个方向的控制极其简单（假设矩阵名为s,横坐标为x，纵坐标为y）：

斜向上：s[x--][y++]
斜向下：s[x++][y--]

确定了沿方向填充的语句，填充完成，下一步就是转换方向，索引必须进入虚界方可。下图展示两个方向在填充时会进入的虚界。

认真观察即可发现虚界与正确索引的校正关系！如下所示：

此处要分类讨论：

位置\校正操作\填充方向	斜向上	斜向下
上三角	++x	++y
下三角	x+=2,--y	y+=2,--x

根据上表我们可以将进入虚界的索引校正回来，然后进行下一个方向的填充！但真的是这样吗？

请注意主对角线的处理，你是将它看成上三角的一部分还是下三角的一部分？

这决定我们在切换上/下三角时需不需要进行额外的校正操作！

如果你将它看成下三角的一部分，那么恭喜你，你不需要额外进行校正。而如果将它看成上三角的一部分，那么你需要校正！

为简单起见（且这也可以通过图示看出来为什么要将主对角线看成下三角的一部分，因为主对角线的校正方法很明显属于下三角），我们将主对角线划归下三角，就不化简为繁了（虽然只会多一个if else结构，但我就是不想加，哎）

最后一个阶段了！我们此时要确定到底什么时候是斜向上？什么时候是斜向下？

设置计数器k,从0开始计数。下图每个格子右下角表示k的值

可以轻易看出，当k为奇数时，方向为斜向下，为偶数时为斜向下！这不随输入矩阵维数n变化！

蛇形矩阵的逻辑就这么完了！图示过程如下：

code

#include <iostream>
#include <vector>
using namespace std;
class Solutions{
public:
    vector<vector<int>> Snake(const int& n) {
        vector<vector<int>> snake(n, vector<int>(n));
        int num = 1;
        int x = 0, y = 0;
        int flag;
        for (int k = 0; k < 2 * n; ++k) {
            flag = k >= n - 1 ? 1 : 0;
            if (!flag) {//上三角
                if (!(k & 1)) {//斜向上
                    while (x >= 0)
                        snake[x--][y++] = num++;
                    ++x;
                }
                else {//斜向下
                    while (y >= 0)
                        snake[x++][y--] = num++;
                    ++y;
                }
            }
            else {//下三角
                if (!(k & 1)) {//斜向上
                    while (y < n)
                        snake[x--][y++] = num++;
                    x += 2, --y;
                }
                else {//斜向上
                    while (x < n)
                        snake[x++][y--] = num++;
                    y += 2, --x;
                }
            }
        }
        return snake;
    }
    void ShowMatrix(const vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j)
                printf("%4d ", matrix[i][j]);
            cout << endl;
        }
    }
};
int main() {
    int n;
    cin >> n;
    Solutions s;
    vector<vector<int>> m(n, vector<int>(n));
    m = s.Snake(n);
    s.ShowMatrix(m);
    return 0;
}

效果

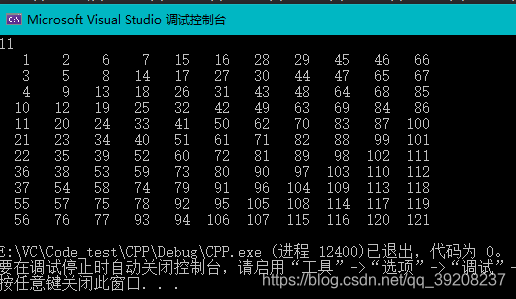
结语

有时候做题，我们需要深入剖析里面的逻辑，要搞清楚为什么这样是正确的，那样是不正确的。只有深入了解里面的各种逻辑，我们才能写出比较好的代码。

更新——蛇形矩阵另一种的解题方法

该解法来自一位王姓妹纸！使用java完成，支持非正方形蛇形矩阵,感兴趣的童鞋可以仔细研究一下：

static int count = 0;
public static int[][] SnakePrintArr(int m, int n)
{
	if (m == 0 || n == 0)
		return null;
	int x1 = 0;
	int x2 = 0;
	int y1 = 0;
	int y2 = 0;
	boolean fromUp = true;
	int[][] arr = new int[m][n];
	while (y2 < m){
		fromUp = !fromUp;
		PrintALine(arr, x1, x2, y1, y2, fromUp);
		x1 = (y1 == arr[0].length - 1) ? ++x1 : x1;
		y1 = (y1 == arr[0].length - 1) ? y1 : ++y1;
		y2 = (x2 == arr.length - 1) ? ++y2 : y2;
		x2 = (x2 == arr.length - 1) ? x2 : ++x2;
		//System.out.println(x1);
	}
	return arr;
}
public static void PrintALine(int[][] arr, int x1, int x2, int y1, int y2, boolean fromUp){
	if (fromUp)
		while (x1 <= x2)
			arr[x1++][y1--] = ++count;
	else
		while (x2 >= x1)
			arr[x2--][y2++] = ++count;
}