回归分析-常用统计量含义解析

最新推荐文章于 2024-04-09 18:52:09 发布

kelly_zero

最新推荐文章于 2024-04-09 18:52:09 发布

阅读量2w

点赞数 11

分类专栏：统计学基础文章标签：回归分析统计量 AIC BIC 回归系数标准差

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_39284106/article/details/104170331

版权

线性回归模型预测好坏，评判标准主要观察回归直线与各观测点的接近程度（即直线的拟合优度）。但是如何量化它们之间的接近程度呢？可使用以下常用统计量进行衡量。各统计量分解如下：

SST总平方和 $\large SST=\sum \left (y_{i} -\bar{y}\right )^{2}$
SSR回归平方和 $\large SSR=\sum \left (\widehat{y}_{i} -\bar{y}\right )^{2}$
SSE残差平方和 $\large SSE=\sum \left (y_{i} -\widehat{y}_{i}\right )^{2}$

回归平方和是回归值与均值的离差平方和，可以看做由于自变量 $\large x$ 的变化引起的 $\large y$ 的变化（即 $\large y$ 受 $\large x$ 的影响）；

残差平方和（或称误差平方和）是真实值与回归值的离差平方和，它是除了 $\large x$ 对 $\large y$ 的线性影响之外的其他因素引起的 $\large y$ 的变化部分，是不能由回归直线来解释的 $\large y_{i}$ 的变差部分（即 $\large y$ 受其他因素的影响，如 $\large x$ 对 $\large y$ 的非线性影响、测量误差等）。残差平方和描述了真实值与预测值之间的差异程度。

三个平方和的关系为：

总平方和（SST）= 回归平方和（SSR）+ 残差平方和（SSE）

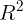判定系数 $\large R^{2}=\frac{SSR}{SST}=\frac{\sum \left (\widehat{y}_{i} -\bar{y}\right )^{2}}{\sum \left (y_{i} -\bar{y}\right )^{2}} = 1-\frac{\sum \left (y_{i} -\widehat{y}_{i}\right )^{2}}{\sum \left (y_{i} -\bar{y}\right )^{2}}$

判定系数 $\large R^{2}$ 是对估计的回归方程拟合优度的度量。（即测度了回归直线对观测数据的拟合程度）

若所有观测点都落在回归直线上，残差平方和SSE=0，则 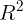$\large R^{2}$ =1，拟合是完全的；
如果 $\large y$ 的变化与 $\large x$ 无关，

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。