wpl=非叶子结点的权值之和
使用上面这个方法的前提是,是一棵huffman树才行,对普通的树没有这个说法。
int wpl = 0;
void WPL(BiTree T) {
if (T != NULL)
{
if (T->lchild || T->rchild) wpl=wpl+T->data;
WPL(T->lchild);
WPL(T->rchild);
}
}
int main() {
BiTree T;
cout << "先序遍历创建二叉树" << endl;
DLR_DG_createTree(T);
//7 3 1 -1 -1 2 -1 -1 4 -1 -1
WPL(T);
cout << wpl;
}
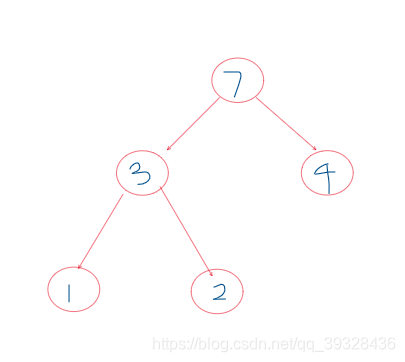
-1代表空节点








 本文探讨了如何计算Huffman树的Weighted Path Length(WPL),即非叶子节点的权值之和。这种方法仅适用于Huffman树,不适用于一般树形结构。在构建Huffman树的过程中,WPL是一个重要的指标。
本文探讨了如何计算Huffman树的Weighted Path Length(WPL),即非叶子节点的权值之和。这种方法仅适用于Huffman树,不适用于一般树形结构。在构建Huffman树的过程中,WPL是一个重要的指标。

















 5468
5468

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










