经典算法思想1——动态规划( Dynamic Programming)

转自：做大饼馅儿的韭菜

动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。通俗的说，就是通过记住已经求出的解并在这些解的基础之上求解下一步。

动态规划求解方式有两种：1.自顶向下的备忘录法；2.自底向上。

1 def febonacci(n):
2     if n<=0:return 0
3     elif n==1:return 1
4     return febonacci(n-1)+febonacci(n-2)

上面的代码是采用的递归的形式，实线斐波那契数列，通过对递归过程进行剖析，

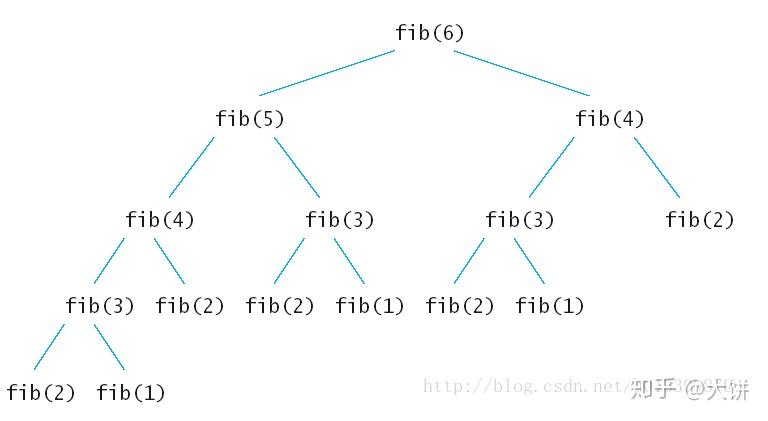
                                                            斐波那契递归过程

 

以上为斐波那契数列为6的时候的递归过程，从这个过程可以看出例如fib(2)，fib(3)都被重复执行了很多次，这就导致了计算资源的浪费，另外空间开销也不小，通过使用动态规划的思想来与递归方法做一个比较。

自顶向下的备忘录法

创建一个n+1大小的数组来保存求出的斐波那契数列中的每一个值，在递归的时候如果发现前面的fib(n)的值计算出来了就不再计算，如果未计算出来，则计算出来后保存在Memo数组中，下次调用fib(n)时候就不会重新递归。

 1 def dynamic_fabonacci(n):
 2     Memo=[-1]*n
 3     if n<=0:return n
 4     return fib(n-1,Memo)
 5 def fib(n,Memo=[]):
 6     Memo=list(Memo)
 7     if Memo[n]!=-1:return Memo[n]    #如果之前已经算过了，则直接读取，无需重复计算
 8     if n<=1:Memo[n]=1   #前2位记录为1
 9     else:Memo[n]=fib(n-1,Memo)+fib(n-2,Memo)   #递归，区分与纯递归方法的区别，这里避免了很多重复计算
10     return Memo[n]

自底向上

备忘录法还是利用了递归的方式，计算到fib(6)的时候，然后要计算出fib(1),fib(2)...，自底向上的算法是从头开始进行，先计算出fib(1),fib(2)...,这是动态规划的核心，先计算子问题，再由子问题计算父问题。

1 def dynamic_fabonacci(n):
2         flist=[-1]*n;flist[0]=flist[1]=1
3         if n<=0:return n
4         for i in range(2,n):
5             flist[i]=flist[i-1]+flist[i-2]   #基于之前列表已经计算出的结果基础之上计算后续
6         return flist[n-1]

一般来说由于备忘录方式的动态规划方法使用了递归，递归的时候会产生额外的开销，使用自底向上的方法比自顶向下备忘录的方法更好。

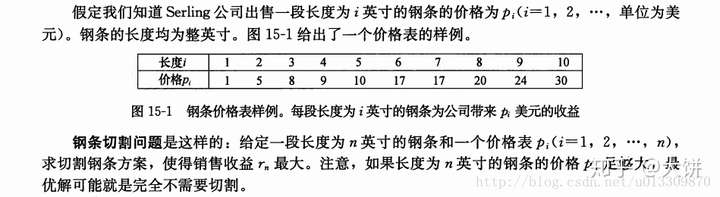
这里举一个动态规划的例子：

 1 def cut1(n):    #第一种方法，递归
 2     l = []
 3     if n<=1:return n
 4     p=10 if n>10 else n
 5     for i in range(p):
 6         l.append(l2[i]+cut1(n-l1[i]))
 7     q=np.max(l)
 8     return q
 9 
10 def cut2(n):  #第二种方法，动态规划，自顶向下备忘录法
11     t=[-1]*n;l=[]
12     if n<1:return n
13     if t[n-1]!=-1:return t[n-1]
14     p=10 if n>10 else n
15     for i in range(p):
16         l.append(l2[i]+cut2(n-l1[i]))
17     t[n-1]=np.max(l)
18     return t[n-1]
19 '''自顶向下的备忘录其实就是在递归的过程中记录下已经调用过的子函数的值'''
20 
21 def cut3(n):   #第三种方法，自底向上的动态规划法
22     t=[-1]*n;l=[]
23     if n<1:return 0
24     for i in range(n):    #求出每个长度下最优分割方案，并记录到数组t中
25         p = 10 if i >= 10 else i+1
26         for j in range(p):
27             if i ==j:l.append(l2[j])
28             else:l.append(l2[j]+t[i-l1[j]])   #遍历分割方案
29         t[i]=np.max(l)   #记录最优方案
30         l=[]   #将列表清空，重新下一轮
31     return t[n-1]
32 '''自底向上的方法首先会求出小于n时每一个长度对应的最优解，在此基础之上再算出长度为n时的最优解，
33 这里属于最优子结构问题：一个问题取得最优解的时候，它的子问题也一定要取得最优解'''

动态规划原理

1.最优子结构(自底向上)

用动态规划求解最优化问题第一步就是刻画最优解的结构，如果一个问题的解结构包含其子问题的最优解，称此问题具有最优子结构的性质。是否某个问题适合使用动态规划来求解就是看是否具有最优子结构的性质。使用动态规划算法时，用子问题的最优解来构造原问题的最优解。

2.重叠子问题(自顶向下的备忘录)

如果递归算法反复求解相同的子问题，就称为具有重叠子问题性质。在动态规划算法中使用数组来保存子问题的解，这样子的问题多次求解的时候可以直接查表不用调用函数递归。

动态规划的经典模型

线性模型

线性模型是动态规划中最常用的模型，上文说到的钢条切割问题就是经典线性模型，这里的线性是指状态的排布是呈线性的。

区间模型

区间模型的状态表示一般为d[i][j]，表示区间[i,j]上的最优解，然后通过状态转移计算出[i+1,j]或者[i,j+1]上的最优解，逐步扩大区间的范围，最终求得[1,len]的最优解。

背包模型 https://blog.csdn.net/u013309870/article/details/75193592

有N种物品（每种物品1件）和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。决策为第i个物品在前i-1个物品放置完毕后，是选择放还是不放，状态转移方程为：f[i][v] = max{ f[i-1][v], f[i-1][v – Ci] +Wi }

时间复杂度O(VN)，空间复杂度O(VN) （空间复杂度可利用滚动数组进行优化达到O(V) ）。

动态规划是一种解决问题的思维方式，想要彻底掌握还需要进行大量的练习，养成一种思维习惯。同时，动态规划无论是求职面试，还是以后面对各种问题，都是非常重要的思想必须牢牢掌握。

参考博客：

https://blog.csdn.net/u013309870/article/details/75193592​blog.csdn.net/u013309870/article/details/75193592