代码随想录——冗余连接II（并查集）

题目

在本问题中，有根树指满足以下条件的 有向
图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n
中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi
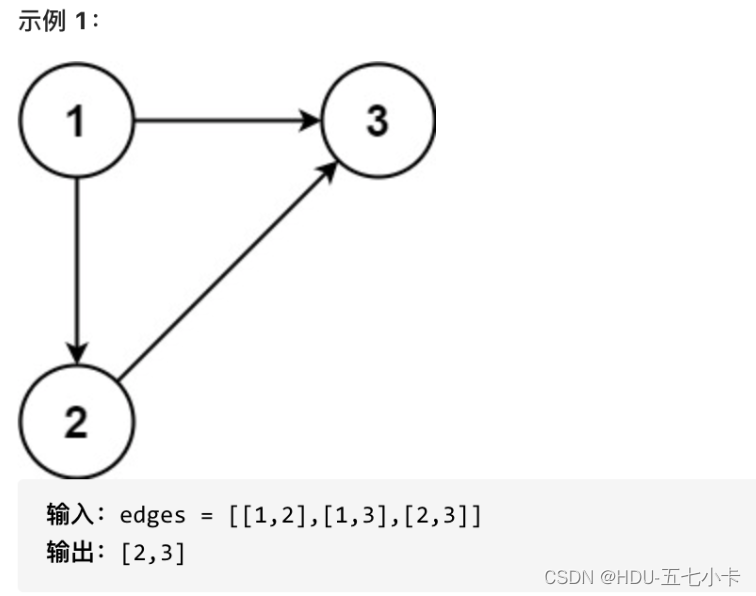
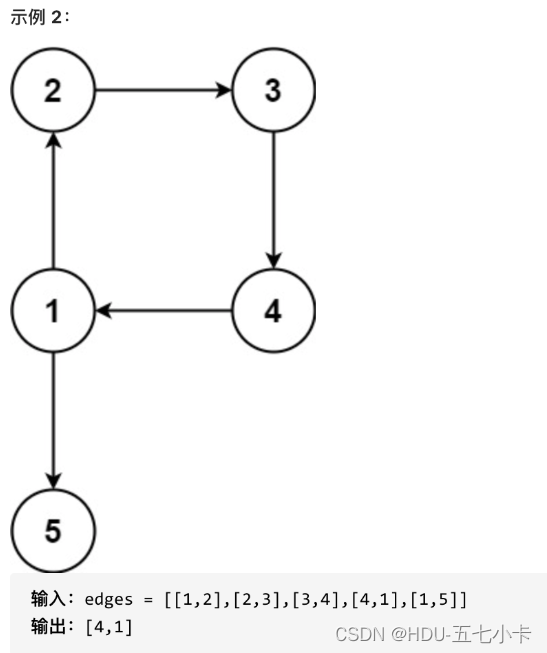
的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。


提示：

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ui, vi <= n

思路

本题相比冗余连接的区别就是变成了有向图

1. 如果图中没有入度为2的节点，那么图中一定有有向环，要找到删除的边相当于找到构成环的那条边
2. 对于图中入度为2的节点，一定是删除指向入度为2的节点的两条边其中的一条，如果删了一条后，判断如果这个图是一个树，那么这条边就是答案，同时注意要从后向前遍历，因为如果两条边删哪一条都可以成为树，就删最后那一条。

所以两个最关键的函数：

• isTreeAfterRemoveEdge() 判断删一个边之后是不是树了
• getRemoveEdge() 确定图中一定有了有向环，那么要找到需要删除的那条边，使其变成树

判断一个图是不是树，这里要用到并查集，因为在两个节点添加边之前，就可以在并查集中找到的话，添加这条边之后，这个图一定不是树，因为两个节点已经在集合中，这两个点之间的边就是冗余连接

java代码如下：

class Solution {
	private static final int N= 1000;
	private int[] father;
	public Solution {	
		father = new int[N];
		// 并查集初始化
		for(injt i = 0; i < N; i++){
			father[i] = i;
		}
	}
	
	// 并查集里寻根的过程
	private int find(int u){
		if(u == father[u]){
			return u;
		}
		father[u] = find(father[u]);
		return father[u];
	}
		
	// 将v->u 这条边加入并查集
	private void join(int u , int v){
		u = find(u);
		v= find(v);
		if(u == v) return;
		father[v] = u;
	}
	
	// 判断 u 和 v是否找到同一个根,即是否是同一个集合
	private boolean same(int u, int v){
		u = find(u);
		v = find(v);
		return u == v;
	}
	

    private void initFather() {
        // 并查集初始化
        for (int i = 0; i < N; ++i) {
            father[i] = i;
        }
    }

	//判断删一条边之后判断是不是树,deleteEdge 表示要删除的边
	private boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEgde){
		initFather();
		for(int i = 0; i < edges.length; i++){
			if(i == deleteEdge) continue;
			if(same(edges[i][0],edges[i][1])){//如果第i条边的两个节点在同一个集合内，那么这条边一定是冗余连接，会构成有向环，一定不是树
				return false;
			}
			join(edges[i][0],edges[i][1]);//否则加入集合中
		}
		return true;
	}
	
	//在有向图里找到删除的那条边，使其变成树
	private int[] getRemoveEdge(int[][] edges) {
        initFather();
        for(int i = 0; i < edges.length; i++) {
            if(same(edges[i][0], edges[i][1])) { // 构成有向环了，就是要删除的边
                return edges[i];
            }
            join(edges[i][0], edges[i][1]);
        }
        return null;
    }


	public int[] findRedundantDirectedConnection(int[][] edges){
		int[] inDegree = new int[N];//统计入度
		for(int i = 0; i < edges.length; i++){
			inDegree[ edges[i][1] ] += 1;//edges[i][1]表示结尾的那个节点，相当于有别的节点指向自己，所以入度加一 
		}
			
		 // 找入度为2的节点所对应的边，注意要倒序，因为优先返回最后出现在二维数组中的答案
		 ArrayList<Integer> twoDegree = new ArrayList<Integer>();
		 for(int i = deges.length - 1; i >= 0; i--){
		 	if(inDegree[ edges[i][1] == 2 ]){//如果该节点的入度为2
		 		twoDegree.add(i);//把两条边都加入进来
		 	}
		 }
		 	
		 // 如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树
		 if(!twoDegree.isEmpty()){
		 	if(isTreeAfterRemoveEdge(edges, twoDegree.get(0))){
		 		return edges[ twoDegree.get(0) ];
		 	}
		 	return edges[ twoDegree.get(1) ];
		}
		
		//明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了
		return getRemoveEdge(edges);
	}
}