svm

参考：https://zhuanlan.zhihu.com/p/41952687

线性SVM

先看下线性可分的二分类问题

(a)是已有的数据，红色和蓝色分别代表两个不同的类别。数据显然是线性可分的，但是将两类数据点分开的直线显然不止一条。
(b)和©分别给出了两种不同的分类方案，其中黑色实线为分界线，术语称为“决策面”。
每个决策面对应了一个线性分类器。虽然从分类结果上看，两种分类器的效果是相同的。但是他们的性能是有差距的，看下图：

在”决策面”不变的情况下，我又添加了一个红点（箭头指示）。
可以看到，分类器A依然能很好的分类结果，而分类器B则出现了分类错误。
显然分类器A的”决策面”放置的位置优于分类器B的”决策面”放置的位置，SVM算法也是这么认为的，它的依据就是分类器B的分类间隔比分类器C的分类间隔大。
这里涉及到第一个SVM独有的概念”分类间隔”。
两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔，
拥有最大垂直距离的两条虚线中间的决策面就是SVM要寻找的最优解。
而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为”支持向量”。

（1）”分类间隔”方程

对于一个二维平面的简单例子进行推导。

在上图，我们能获取以下信息：
1）蓝色星星样本用标签-1表示，红色全员样本用+1样本。
2）左边虚线和右边虚线的方程表达式分别为 wx+b=-1 和 wx+b=1
3）决策面即分类线（红线）的表达式为 wx+b=0
直线表达式参考：https://link.zhihu.com/?target=https%3A//blog.csdn.net/u011630575/article/details/78916747
我们的最终目标是求解分类线（红线）： wx+b=0 , 而怎么求这个红线，我们的方法是最大化这两根虚线的距离。从而解得w和b。
两条平行线的方程分别为：

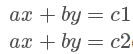
两条平行线的距离d为：

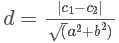
因此，这两根虚线的距离可以表示为

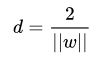
这个d就是”分类间隔”。其中||w||表示w的二范数，求所有元素的平方和，然后再开方。在二维平面的情况下

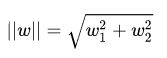
范数参考 https://link.zhihu.com/?target=https%3A//baijiahao.baidu.com/s%3Fid%3D1607333156323286278%26wfr%3Dspider%26for%3Dpc
目标是为了找出一个分类效果好的超平面作为分类器。
分类器的好坏的评定依据是分类间隔 d 的大小，即分类间隔 d 越大，我们认为这个超平面的分类效果越好。

（2）约束条件

为了求解 d 的最大值。我们不得不面对如下问题：
如何判断超平面是否将样本点正确分类？
知道相求距离d的最大值，首先需要找到支持向量上的点，怎么在众多的点中选出支持向量上的点呢？
数学语言对他们进行描述。

这个二维平面上有两种点，我们分别对它们进行标记：
对每个样本点xi加上一个类别标签yi：
$$y_i=\{\begin{array}{c}+1红色点\\ -1蓝色点\end{array}$$
如果我们的超平面方程能够完全正确地对上图的样本点进行分类，就会满足下面的方程：
$$y_i=\{\begin{array}{c}{w}^T{x}_i+b⩾+1,y_i=+1\\ w^T{x}_i+b⩽-1,y_i=-1\end{array}$$
上述公式的解释是，
对于所有分类标签为1的样本点，它们到直线的距离都大于等于1(虚线上的样本点到超平面的距离)。
对于所有分类标签为-1的样本点，它们到直线的距离都小于等于1。
上述方程即给出了SVM最优化问题的约束条件。这时候，可能有人会问了，为什么标记为1和-1呢？因为这样标记方便我们将上述方程变成如下形式：
$$y_i(w^T{x}_i+b)⩾1,i=1,2...$$
因为标签为1和-1，才方便我们将约束条件变成一个约束方程，从而方便我们的计算

（3）线性SVM优化问题基本描述

一开始我们的优化目标为最大化两条虚线的距离：
因为，我们只关心虚线上的支持向量点。随后我们求解d的最大化问题变成了||w||的最小化问题。进而||w||的最小化问题等效于
$$max\frac{2}{||w||}$$
这是为了在进行最优化的过程中对目标函数求导时比较方便，但这绝对不影响最优化问题最后的求解。
我们将最终的目标函数和约束条件放在一起进行描述：
$$min\frac{1}{2}||w|{|}^2$$
缩写s.t.表示”Subject to”，是”服从某某条件”的意思。上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题，同时也是支持向量机的基本数学模型。
$$\begin{gathered} min\frac{1}{2}||w|{|}^2 \\ s.t.y_i \end{gathered}$$