树、二叉树、完全二叉树的区别与基本概念

树、二叉树、完全二叉树的区别与基本概念

一、树

树：不包含回路的连通无向图（树是一种简单的非线性结构）。

                      

树有着不包含回路的特点，所以树就被赋予了很多特性：

1、一棵树中任意两个结点有且仅有唯一的一条路径连通。

2、一棵树如果有n个结点，那它一定恰好有n-1条边。

3、在一棵树中加一条边将会构成一个回路。

4、树中有且仅有一个没有前驱的结点称为根结点。

 

在对树进行讨论的时候将树中的每个点称为结点，

根结点：没有父结点的结点。

叶结点：没有子结点的结点。

内部结点：一个结点既不是根结点也不是叶结点。

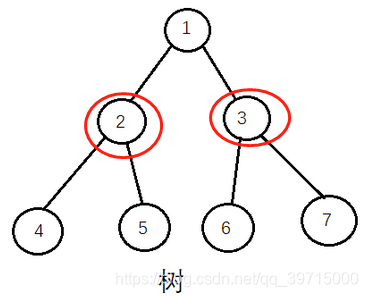
每个结点还有深度，比如上图左边的树的4号结点深度是3（深度是指从根结点到这个结点的层数，根结点为第一层）。

二、二叉树

1、基本概念：

二叉树是一种非线性结构，二叉树是递归定义的，其结点有左右子树之分。

2、二叉树的存储结构：

二叉树通常采用链式存储结构，存储结点由数据域和指针域（指针域：左指针域和右指针域）组成，二叉树的链式存储结构也称为二叉链表，对满二叉树和完全二叉树可按层次进行顺序存储。

 

特点：

1、每个结点最多有两颗子树。

2、左子树和右子树是有顺序的，次序不能颠倒。

3、即使某结点只有一个子树，也要区分左右子树。

4、二叉树可为空，空的二叉树没有结点，非空二叉树有且仅有一个根节点。

二叉树中有两种特殊的二叉树：满二叉树、完全二叉树。

（满二叉树的严格的定义是：一颗深度为h且有2h-1个结点的二叉树）

完全二叉树：除最后一层外，每一层上的节点数均达到最大值，在最后一层上只缺少右边的若干结点完全二叉树的形状类似于下图

为了方便理解请看下图

二叉树相关词语解释：

结点的度：结点拥有的子树的数目

叶子结点：度为0的结点（tips：在任意一个二叉树中，度为0的叶子结点总是比度为2的结点多一个）

分支结点：度不为0的结点

 

树的度：树中结点的最大的度

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1

树的高度：树中结点的最大层次

 

二叉树基本性质：

性质1：在二叉树的第k层上至多有2k-1个结点（k>=1）

性质2：在深度为m的二叉树至多有2m-1个结点

性质3：对任意一颗二叉树，度为0的结点（即叶子结点）总是比度为2的结点多一个

性质4：具有n个结点的完全二叉树的深度至少为[log2n]+1，其中[log2n]表示log2n的整数部分

参考转载链接