一、问题描述
砸金蛋活动,现有三个金蛋A、B、C,其中只有一个有大奖,假设你一开始选择了金蛋B,主持人砸开了金蛋C,里面没有奖,主持人此时问你是否要更换选项,是继续坚持选择金蛋B,还是更改为选择金蛋A?
二、用贝叶斯公式求解
贝叶斯公式: 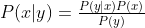
(1) 首先,利用贝叶斯公式计算在C开了的情况下,大奖在B里的概率
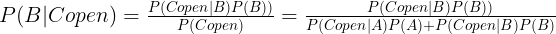
我们设
砸金蛋活动,现有三个金蛋A、B、C,其中只有一个有大奖,假设你一开始选择了金蛋B,主持人砸开了金蛋C,里面没有奖,主持人此时问你是否要更换选项,是继续坚持选择金蛋B,还是更改为选择金蛋A?
贝叶斯公式: 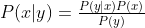
(1) 首先,利用贝叶斯公式计算在C开了的情况下,大奖在B里的概率
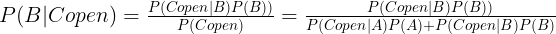
我们设

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


