费马小定理在算法中的意义
1640 年,法国业余数学家 Pierre de Fermat (通常译作“费马”)发现,如果 n 是一个质数的话,那么对于任意一个数 a , a 的 n 次方减去 a 之后都将是 n 的倍数。

例如, 7 是一个质数,于是 27 – 2 、 37 – 3 , 47 – 4 ,甚至 1007 – 100 ,统统都能被 7 整除。但 15 不是质数(它可以被分解为 3 × 5 ),于是 a15 – a 除以 15 之后就可能会出现五花八门的余数了。这个规律在数论研究中是如此基本如此重要,以至于它有一个专门的名字—— Fermat 小定理。作为一个业余数学家, Fermat 发现了很多数论中精彩的结论, Fermat “小”定理只是其中之一。
Fermat 素性测试就是一种比较常用的高效方法,它基于如下原理: Fermat 小定理对一切质数都成立。回想 Fermat 小定理的内容:如果 n 是一个质数的话,那么对于任意一个数 a , a 的 n 次方减去 a 之后都将是 n 的倍数。为了判断 209 是不是质数,我们随便选取一个 a ,比如 38 。结果发现,38209 – 38 除以 209 余 114 (稍后我们会看到,即使把 209 换成上百位的大数,利用计算机也能很快算出这个余数来),不能被 209 整除。于是, 209 肯定不是质数。我们再举一个例子。为了判断 221 是不是质数,我们随机选择 a ,比如说还是 38 吧。你会发现 38221 – 38 除以 221 正好除尽。那么, 221 是否就一定是质数了呢?麻烦就麻烦在这里:这并不能告诉我们 221 是质数,因为 Fermat 小定理毕竟只说了对一切质数都成立,但没说对其他的数成不成立。万一 221 根本就不是质数,但 a = 38 时碰巧也符合 Fermat 小定理呢?为了保险起见,我们不妨再选一个不同的 a 值。比方说,令 a = 26 ,可以算出 26221 – 26 除以 221 余 169 ,因而 221 果然并不是质数。这个例子告诉了我们,如果运气不好的话,所选的 a 值会让不是质数的数也能骗过检测,虽然这个概率其实并不大。因此,我们通常的做法便是,多选几个不同的 a ,只要有一次没通过测试,被检测的数一定不是质数,如果都通过测试了,则被检测的数很可能是质数。没错, Fermat 素性测试的效率非常高,但它是基于一定概率的,有误报的可能。如果发现某个数 n 不满足 Fermat 小定理,它一定不是质数;但如果发现某个数 n 总能通过 Fermat 小定理的检验,只能说明它有很大的几率是质数。
Fermat 素性测试真正麻烦的地方就是,居然有这么一种极其特殊的数,它不是质数,但对于任意的 a 值,它都能通过测试。这样的数叫做 Carmichael 数,最小的一个是 561 ,接下来的几个则是 1105, 1729, 2465, 2821, 6601, 8911… 虽然不多,但很致命。
虽然与本文无关,但有一点不得不提:以 Fermat 的名字命名的东西里,最著名的要数 Fermat 大定理了(其实译作“ Fermat 最终定理”更贴切)。即x^n +y ^n=z ^n 不存在有理数解。
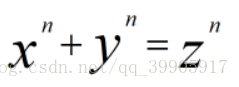
























 7621
7621

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








