【Java】红黑树

一、介绍

红黑树是一种自平衡的二叉查找树，是计算机科学中用到的一种数据结构。

1972年出现，当时被称之为平衡二叉树B树。后来，1978年被修改为如今的 “ 红黑树 ”。

红黑树是一种特殊的二叉查找树，红黑树的每一个节点上都有存储位表示节点的颜色，

每一个节点可以是红色或黑色，不能是其他颜色；红黑树不是高度平衡的，它的平衡是通过 “红黑规则” 进行实现的。

如下图就是一颗红黑树。

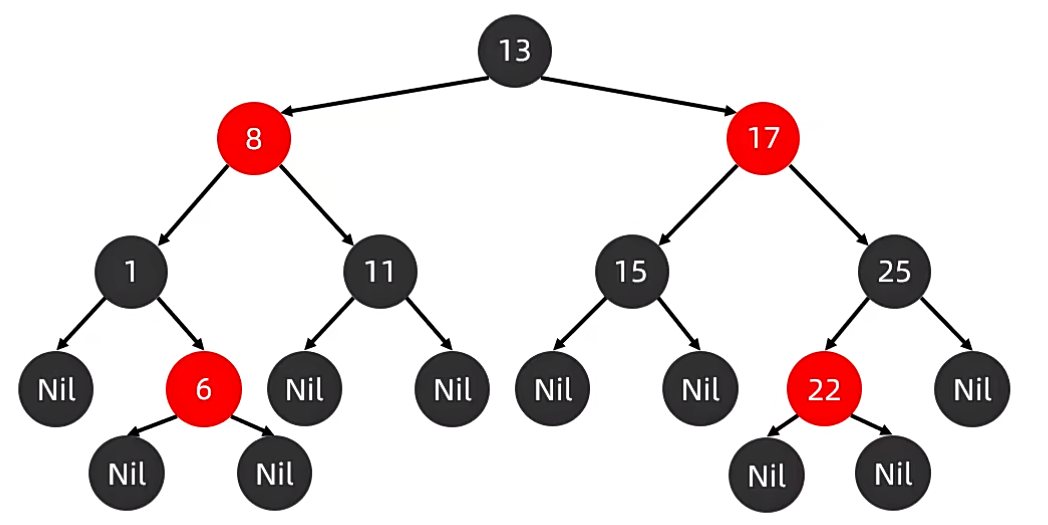
红黑树是一颗二叉查找树，但是它不是一颗平衡二叉树！

平衡二叉树它是高度平衡的，当左右子树高度差超过1时，就会通过旋转保持平衡。因此平衡二叉树的查找效率会比较高，但是它本身也是有一点小弊端的：在添加节点的时候，由于旋转的次数太多了，就会造成添加节点的时间浪费。

但是我们现在要学习的红黑树就是优化了平衡二叉树，改变了规则。

当添加一个节点的时候，如果不符合我自己定义的红黑规则了，才进行旋转或者其他操作，红黑规则会比平衡二叉树的 当左右子树高度差超过1时，就会通过旋转保持平衡 这个规则要轻松一点，没有平衡二叉树这么严格。

---

二、红黑规则

1、每一个节点有可能是红色，也可能是黑色的，不能是其他。

2、根节点必须是黑色。

3、如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为 Nil，这些 Nil 视为叶节点(也叫叶子结点)，每个叶节点(Nil)是黑色的。

4、如果某一个节点是红色，那么它的子节点必须是黑色（即不能出现两个红色节点相连的情况）。

5、对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

---

1、每一个节点有可能是红色，也可能是黑色的，不能是其他。

在之前我们学习的二叉树中，每一个节点中一共有四部分元素

在红色树中，它又多了一个颜色属性，用来记录红黑树结点的颜色，要么是黑色，要么是红色。

---

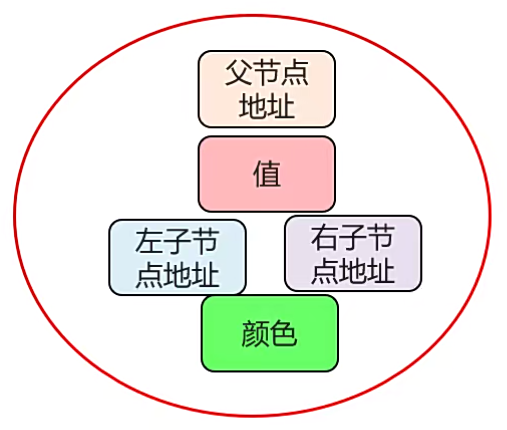
2、如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为 Nil，这些 Nil 视为叶节点(也叫叶子结点)，每个叶节点(Nil)是黑色的

如下图就是一颗红色树。

我们以 6节点 为例，来看看 6 节点里面是什么样子的。

在 6节点 中它首先要记录父节点的地址值，在中间的值中，记录的就是 数字6，颜色就是当前节点真实的颜色。

主要的来看左子节点和右子节点。

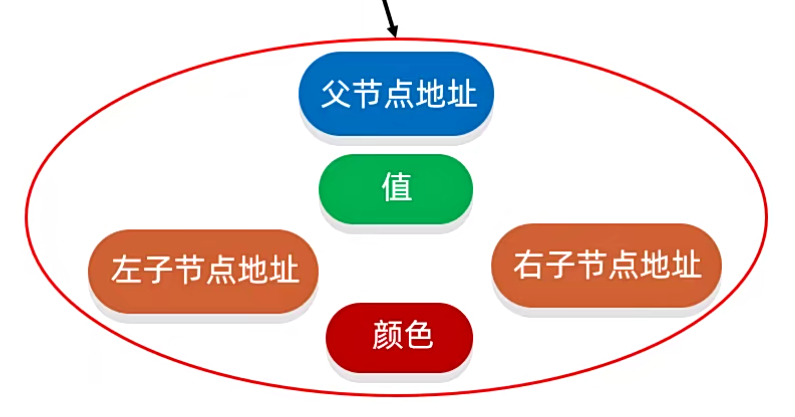
在刚刚我们看见了，它是没有左子也没有右子的，因此它记录的位置就需要记录为空，专业叫做 Nil，你可以把它理解成就是一个 Null。

我们要注意的是，这些 Nil 虽然表示的是空，但是在下面也会挂一个空节点，视为叶子结点，是黑色的。

只不过这些叶子结点里面是没有任何数据的。

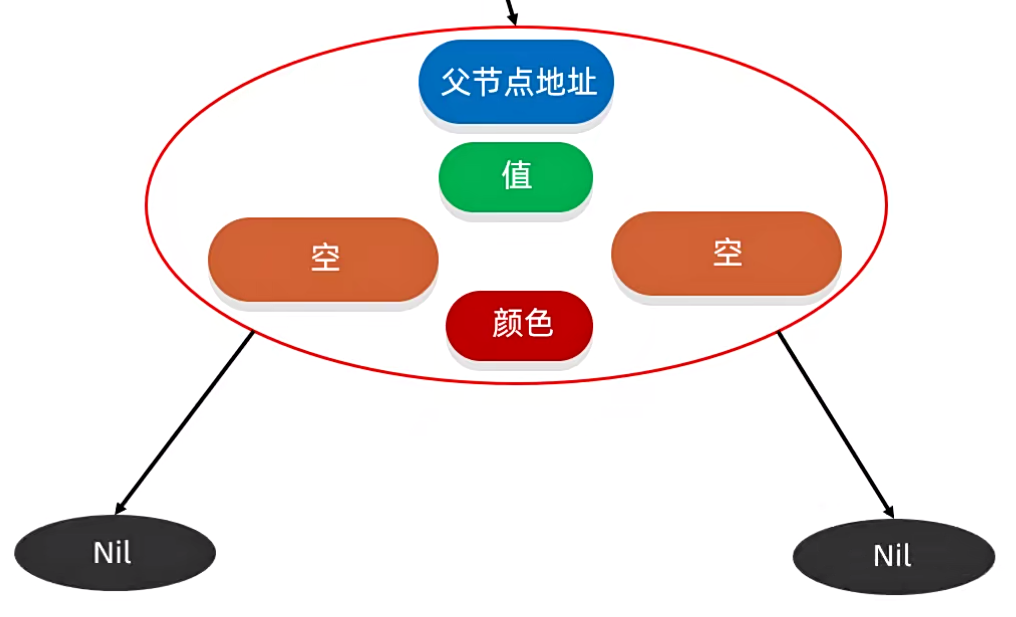
这些叶子结点也是灭有什么意义的，我们平时在 查找数据 / 遍历红色树 的时候，也不会考虑叶子结点。

叶子结点唯一的作用就是待会将上面 第五条红色规则 的时候，用于判断当前红色树是否满足要求的。

---

4、如果某一个节点是红色，那么它的子节点必须是黑色（即不能出现两个红色节点相连的情况）

这句话比较拗口，我们只需要看后面一句话就行了：不能出现两个红色节点相连的情况。

因此，如果两个节点都是黑色，那么是可以在一块的。一红一黑也是可以在一块。只有两个红的不能连在一起。

---

5、对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点

后代节点：以根节点 13 为例，下面所有的节点，都是 13节点 的后代。

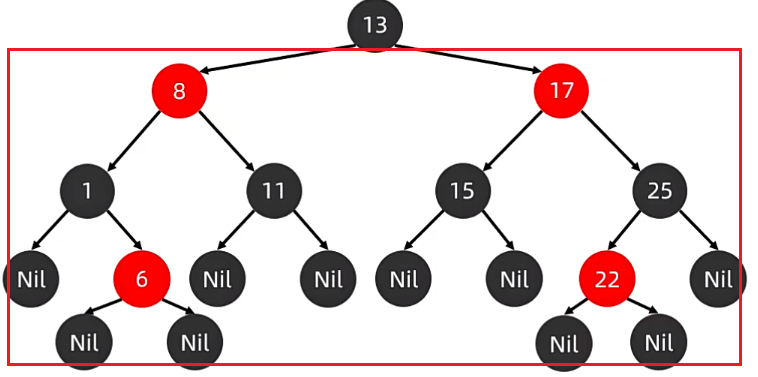
例如以 17节点 为例，17 下面的这些节点都是 17节点 的后代节点。

---

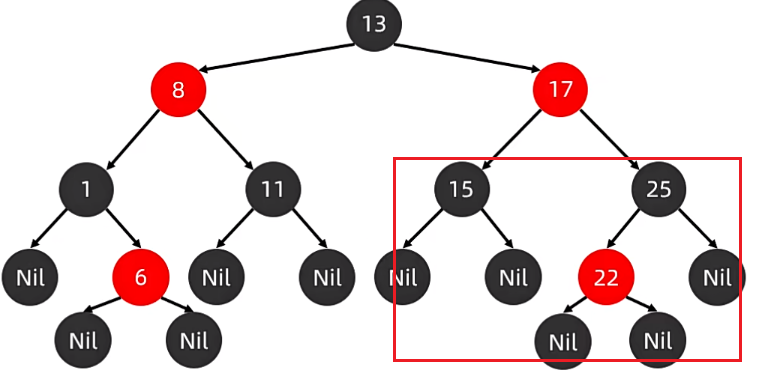
后代叶节点：以 13 为例，只有下面的 Nil 才是 13节点 的后代叶节点

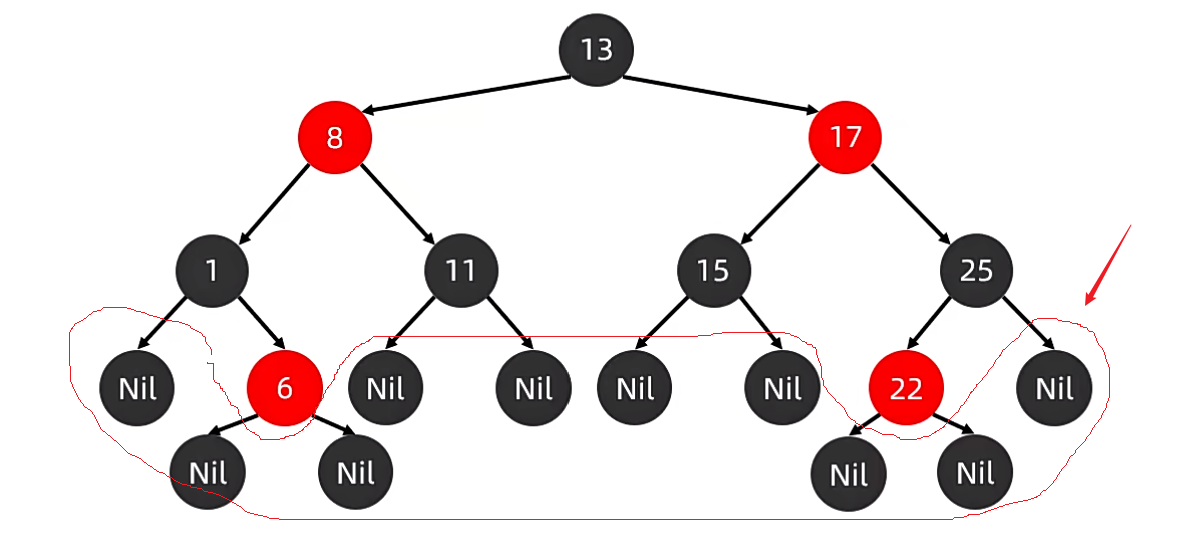
例如以 17节点 为例，17 下面框起来的的这些节点都是 17节点 的后代叶节点。

---

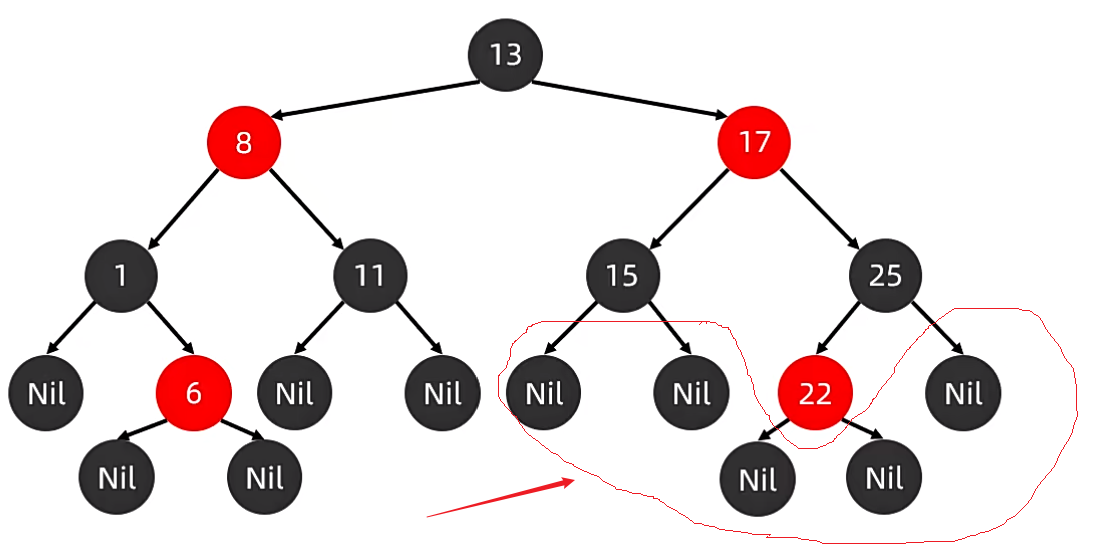
简单路径：以13为例，从13走到8，再走到1，最后走到 Nil，这就是一条简单路径。

核心：只能往前，不能回头。

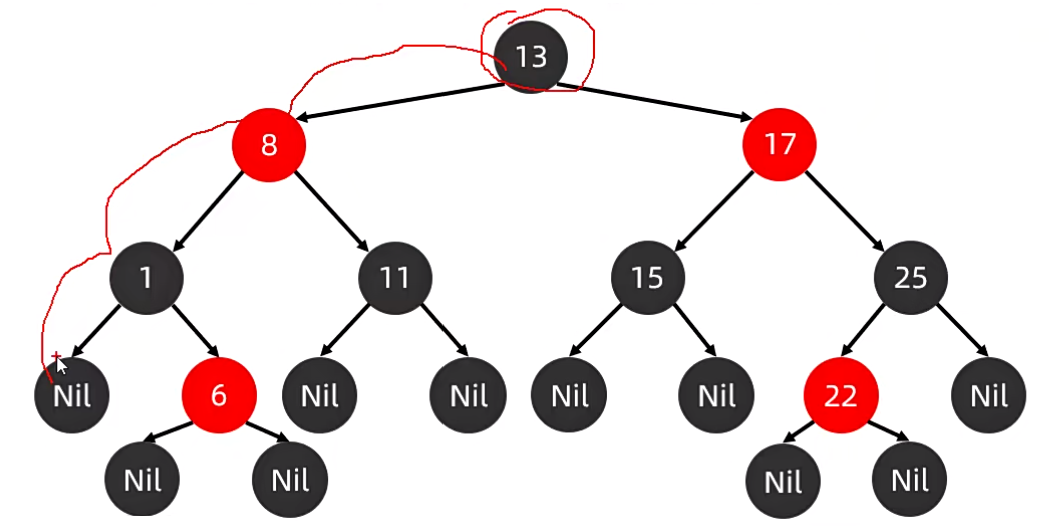
找到简单路径后，这些路径路径上黑色节点的数目是一样的。如上图路径，有三个黑色节点。

因此我们刚刚说的叶子节点 Nil，它本身实际上是没有什么本事的含义的，就是在第五条的规则中用来统计个数的。

---

三、添加节点默认是红色的，因为它的效率高

我们在添加节点的时候需要知道它最基础的要求。

默认颜色：添加节点默认是红色的，因为它的效率高。

假设现在我们要添加 20、18、23 这三个节点。

---

1）假设默认添加的节点默认是黑色的

首先添加第一个节点：20，此时是没有任何问题的，满足红黑规则。

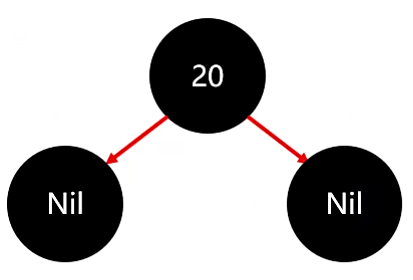
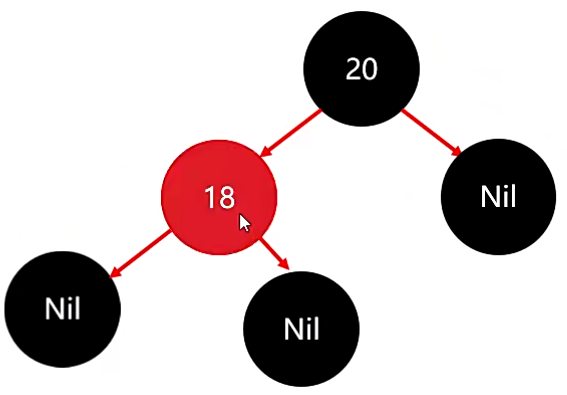
此时来添加第二个节点 18，18 和 20 比较，可以发现 18 比较小，因此需要存入 20 的左边。

注意，此时就已经违背了红色规则：对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。。

以 20根节点 为例，它到左边的 Nil，在这条线上，它一共是三个黑色的节点，但是到右边的 Nil 上，它只有两个黑色的节点。

因此此时不满足这条红黑规则了。

不满足就需要调整：将添加的 18节点 变成红色的就行了。

继续往下，来添加第三个节点 23，23 跟 20 比较，发现比 20 大，因此要存它的右边。

存完了后它其实也违背了刚刚的第五个红黑规则：20 到左边的 Nil ，在这条简单路径上它有两个黑色节点；20 到右边的 Nil，在这条简单路径上一共有三个黑色节点，因此违背了红黑规则。

此时就需要调整：将 23 变成红色的就行了。

由此可见，如果添加的节点默认是黑色的，添加三个元素，就需要调整两次。

---

2）假设默认添加的节点默认是红色的

第一个节点 20 作为根节点，此时就违背了第二条规则：根节点必须是黑色的，因此此时直接将根节点 20 变成黑色的就行了。

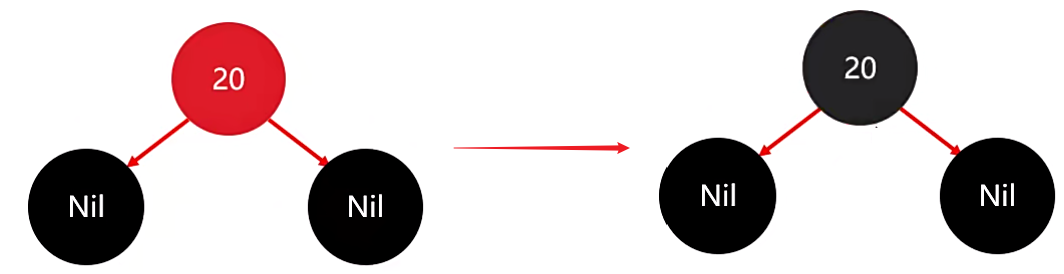
再来添加第二个：18节点，由于 18 小，因此需要存在 20节点 的左边。

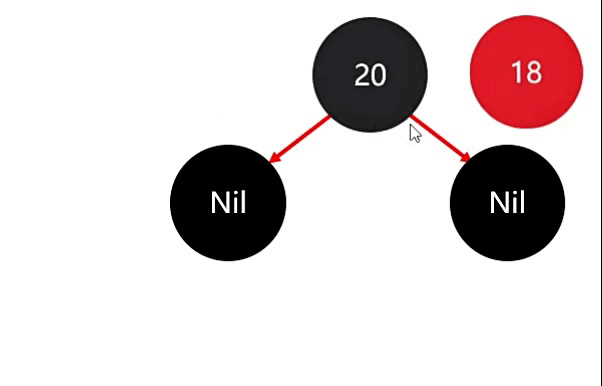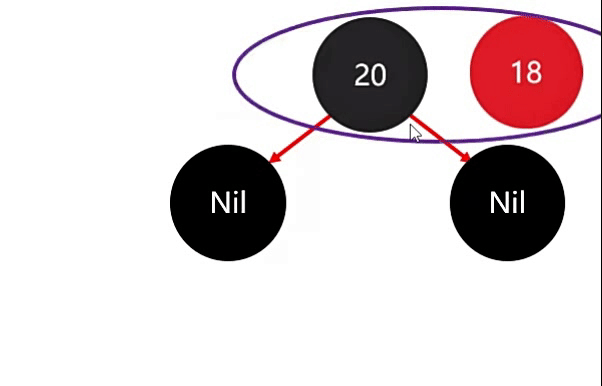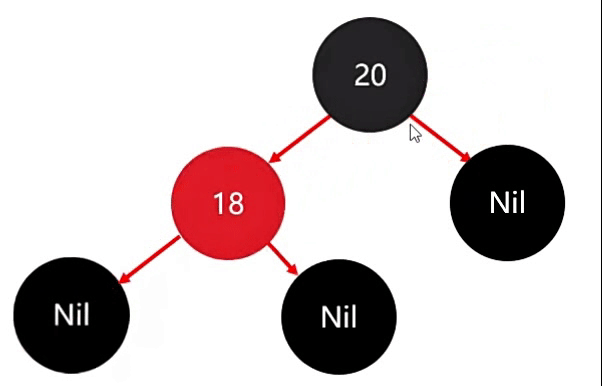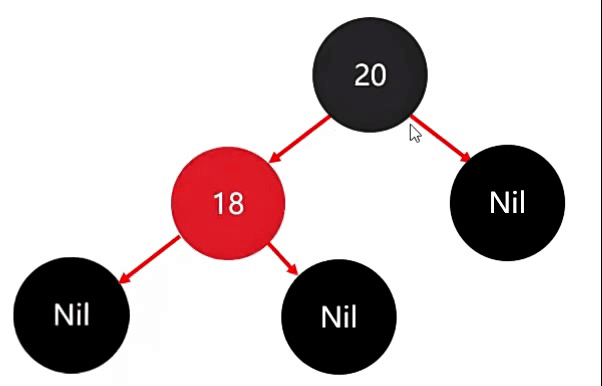
添加完成后，并没有破坏红黑规则，因此此时不需要进行任何调整。

同理，添加第三个节点 23，此时 23 比 20 大，因此存右边。

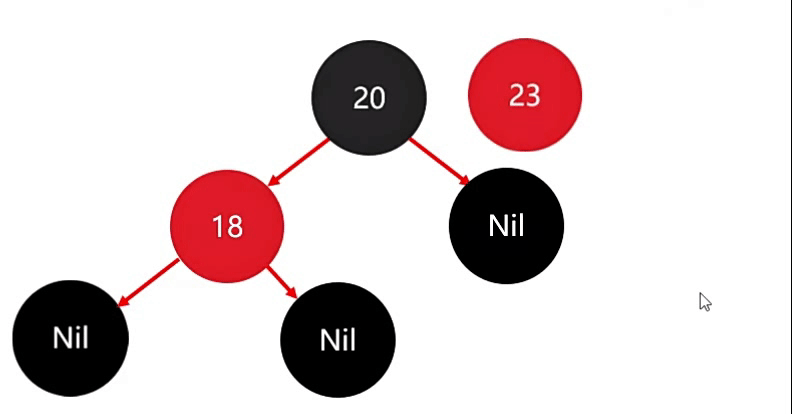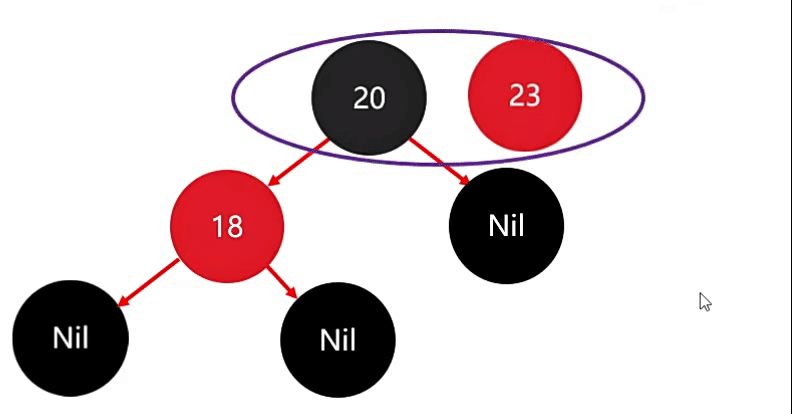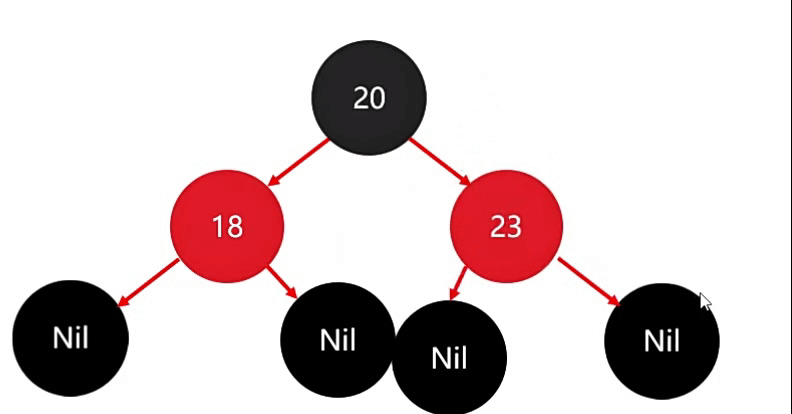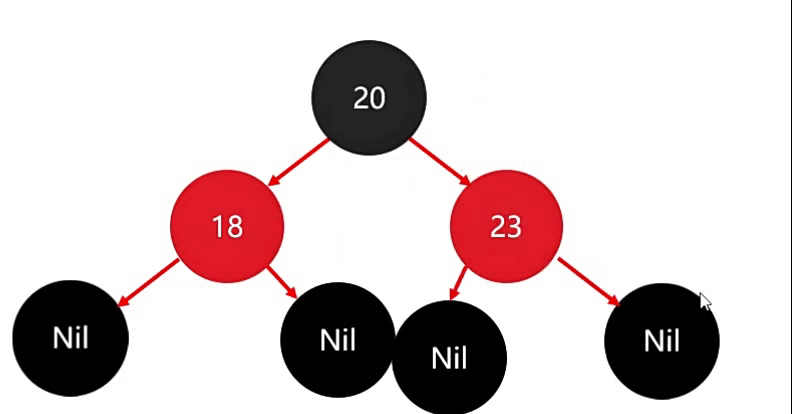
存完后，此时也没有违背红色规则。

因此，添加三个节点，默认是红色的话，只需要调整一次。

此时我们就可以得出一个结论：添加节点时，如果默认颜色是红色的话，这样它的效率要更高。

---

四、红黑树添加节点的规则

我们在往红黑树添加节点的时候，除了要知道，默认是红色之外，其实还有很多种情况会违背红黑规则，不同的情况处理方案是不一样的。

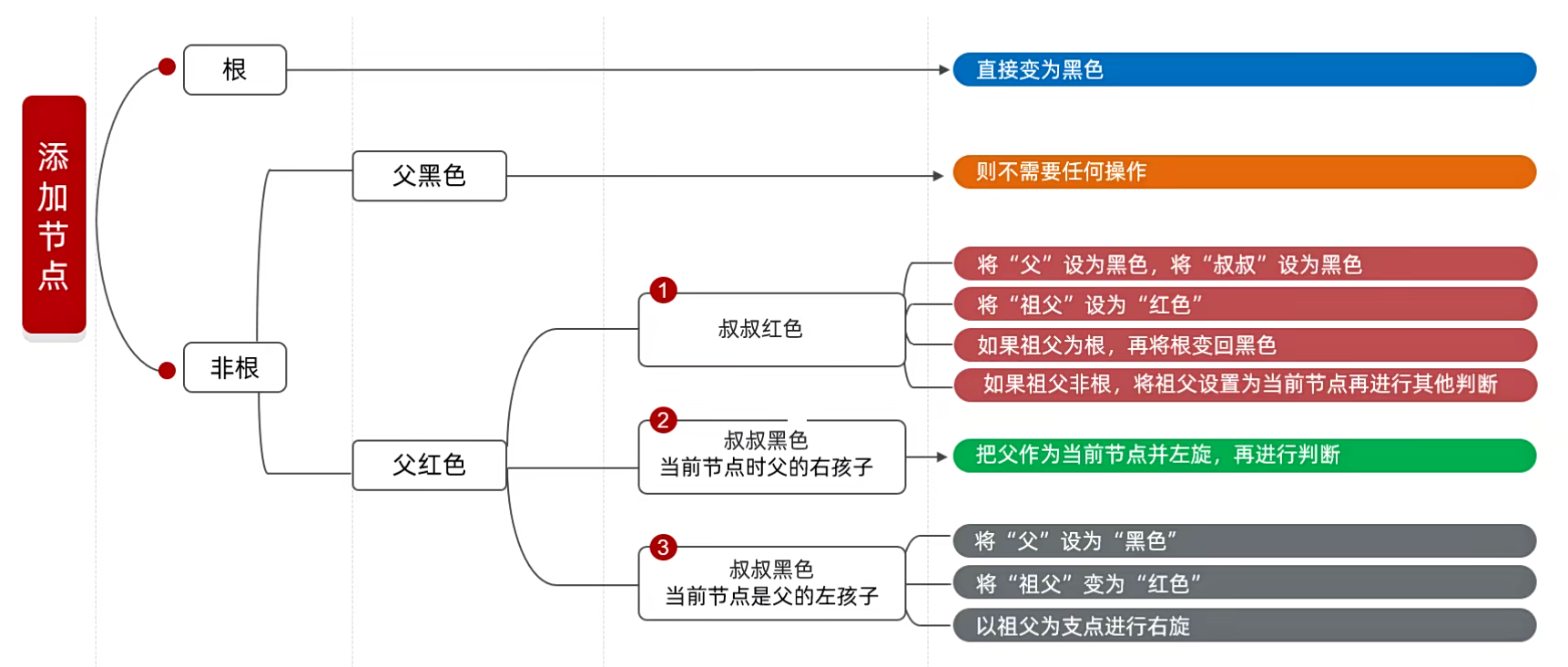
接下来我们系统学习，当我们添加多个节点的时候，红黑树如何调整来保证完全符合红黑规则。

例如添加下面的节点，添加节点默认是红色的，因为它的效率高。

---

1）当前节点为根节点

首先添加 20 作为根节点。

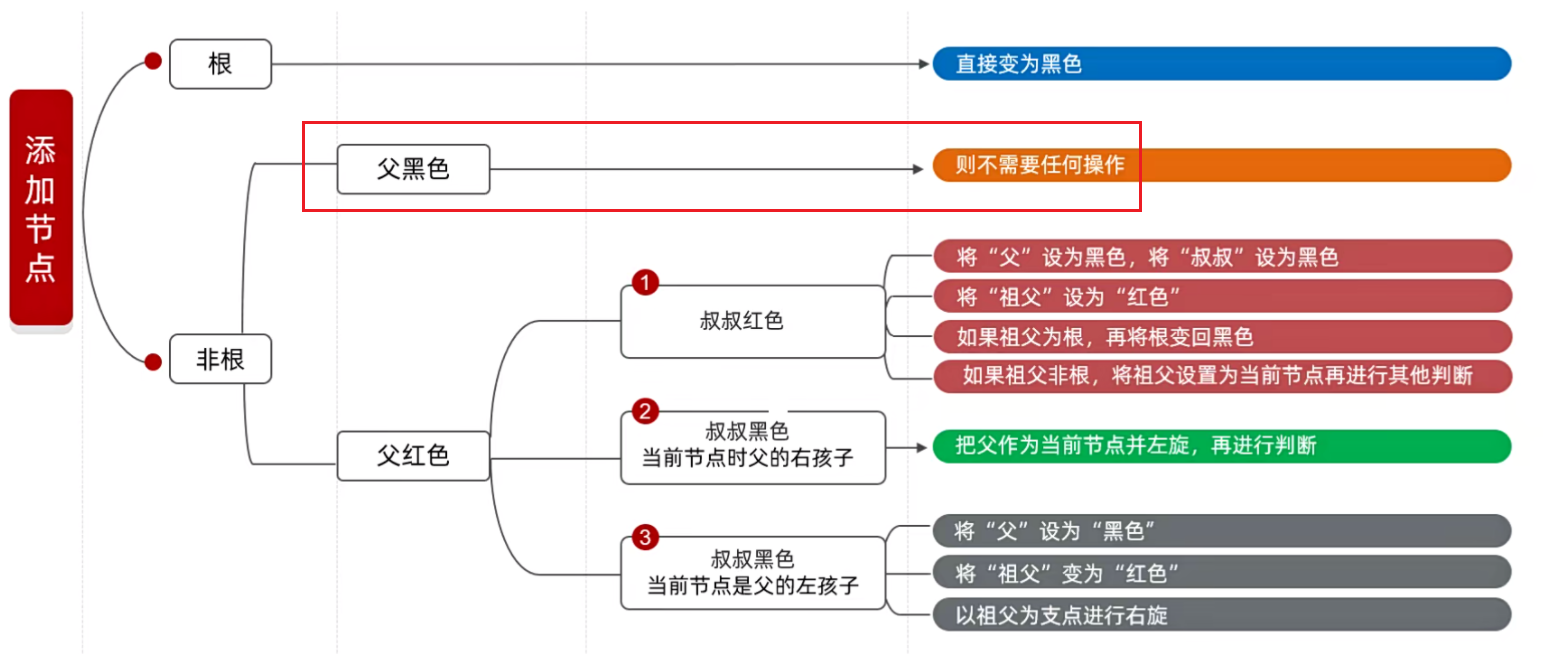
此时它就违背了第二条规则 根节点必须是黑色，此时就可以直接去刚刚的图找处理方案：

如果你在添加节点的时候是根节点，就用蓝色的处理方案 直接变成黑色 。

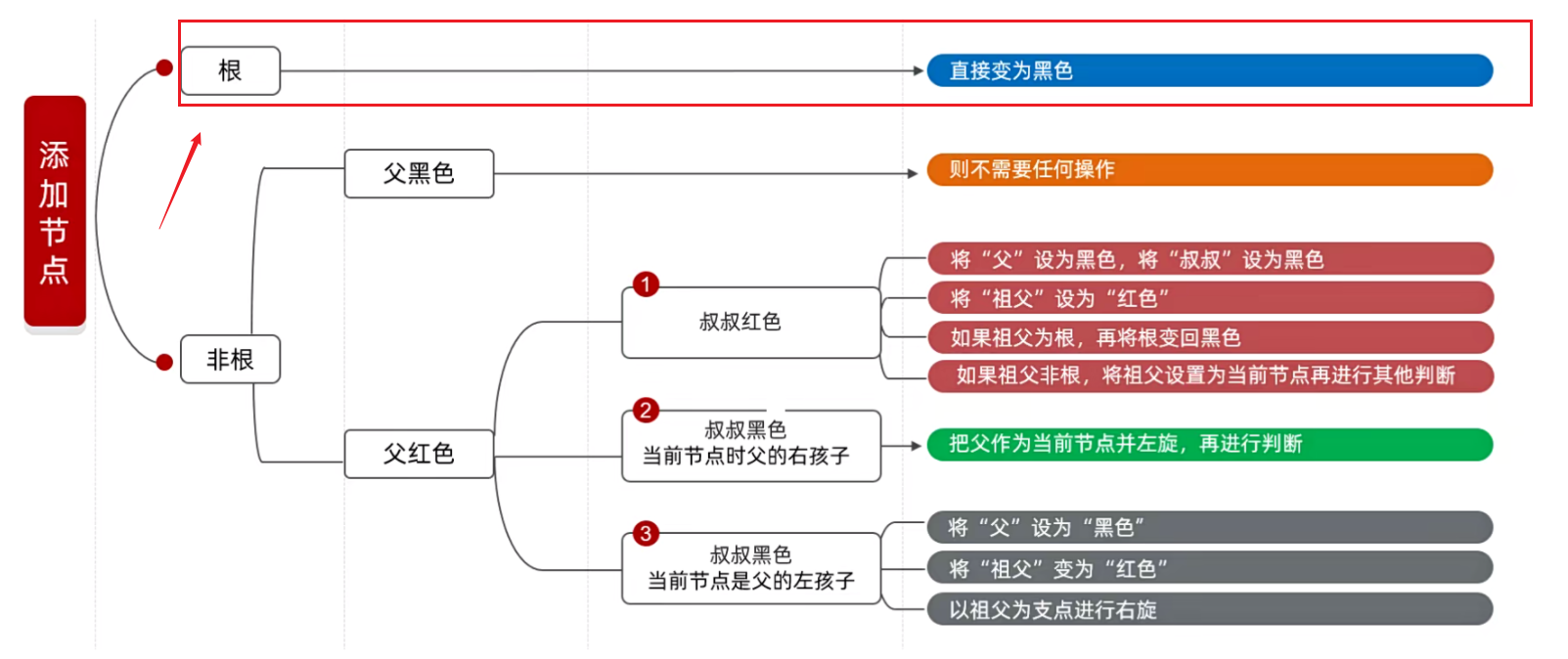
因此此时将 20 变成黑色的，就处理完毕了。

---

2）当前节点不为根节点，父节点为黑色

接下来添加 18节点 ，18 比 20 小，因此存左边。

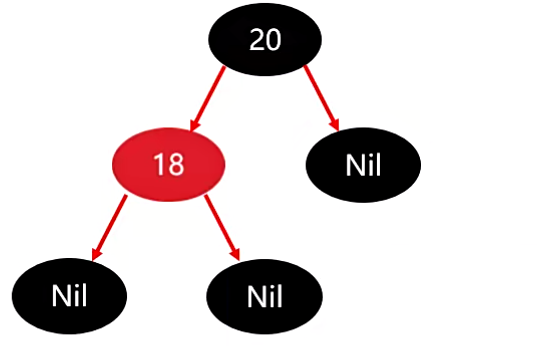
此时是没有违背任何的红黑规则的。

此时在图中也有一个处理方案：如果你添加的节点非根，非根就看它的父节点，如果父节点是黑色的，那么不需要任何操作。

在这我们就知道了，18 的父节点是 20，20 是黑色的，此时我们不需要进行任何的操作。

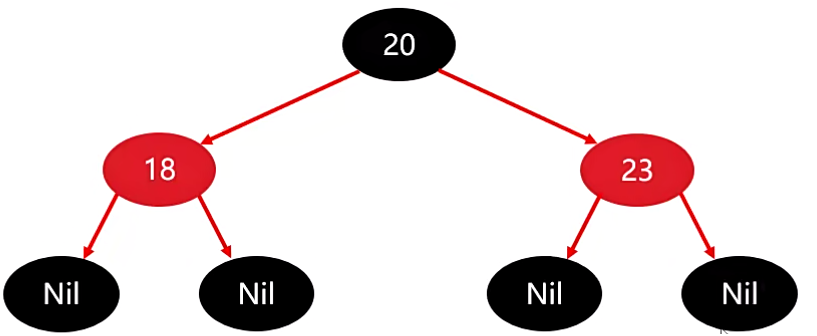
继续往下，添加 23，23 比较后，需要存 20 的右边，由于 23 的父节点 20 也是黑的，因此也不需要进行任何操作。

这个就是前三个节点，相对来讲比较简单。

继续往下，要来添加第四个节点，从这开始，难度就要上升了。

---

3）当前节点不为根节点，父节点为红色，叔叔节点也为红色

开始存 22，首先跟根节点 20 比，发现比 20 大，因此存 20 右边。

右边跟 23 又比了一下，22 小于 23，因此要存 23 的右边。

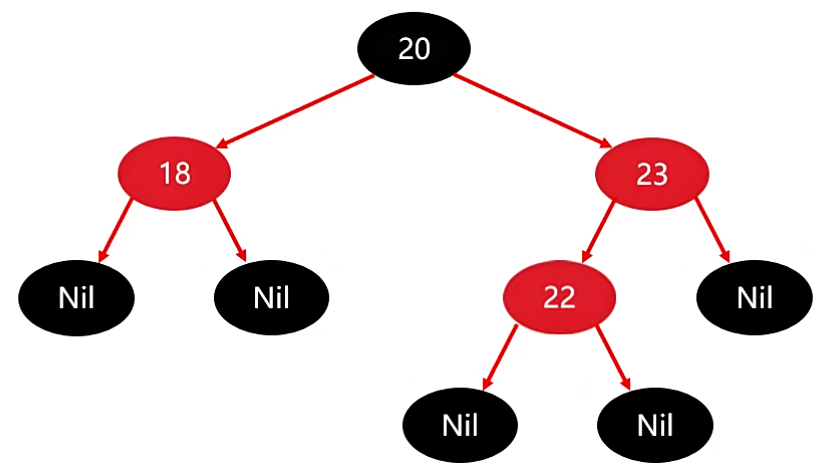
此时就违背了第四条：两个红色节点不能相连。

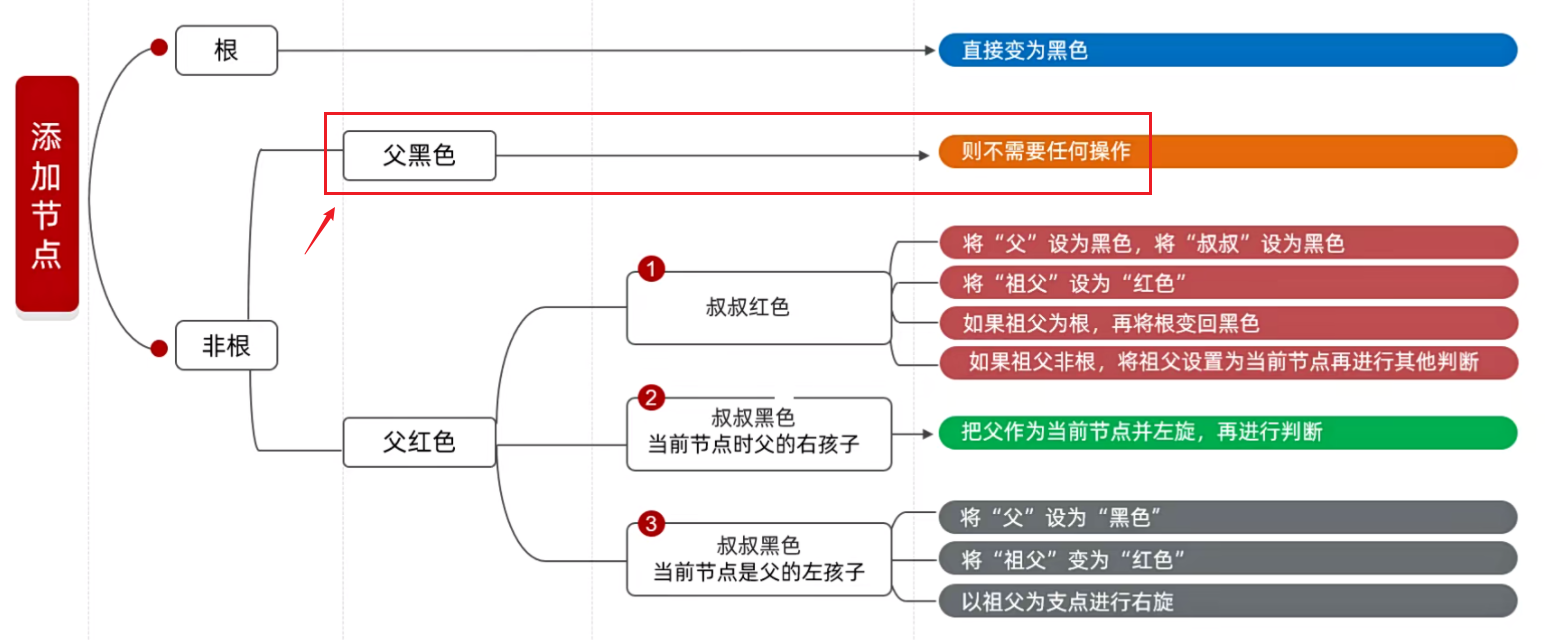
开始看解决方案：如果你添加的节点是非根，就要看父节点，由于父节点是红色的，红色的就需要看叔叔节点。

例如我们刚刚添加的 22 的父节点是 23，那么叔叔节点就是 18，它的颜色是红色。

由于叔叔节点是红色，根据下图，可以看见一共有四种步。

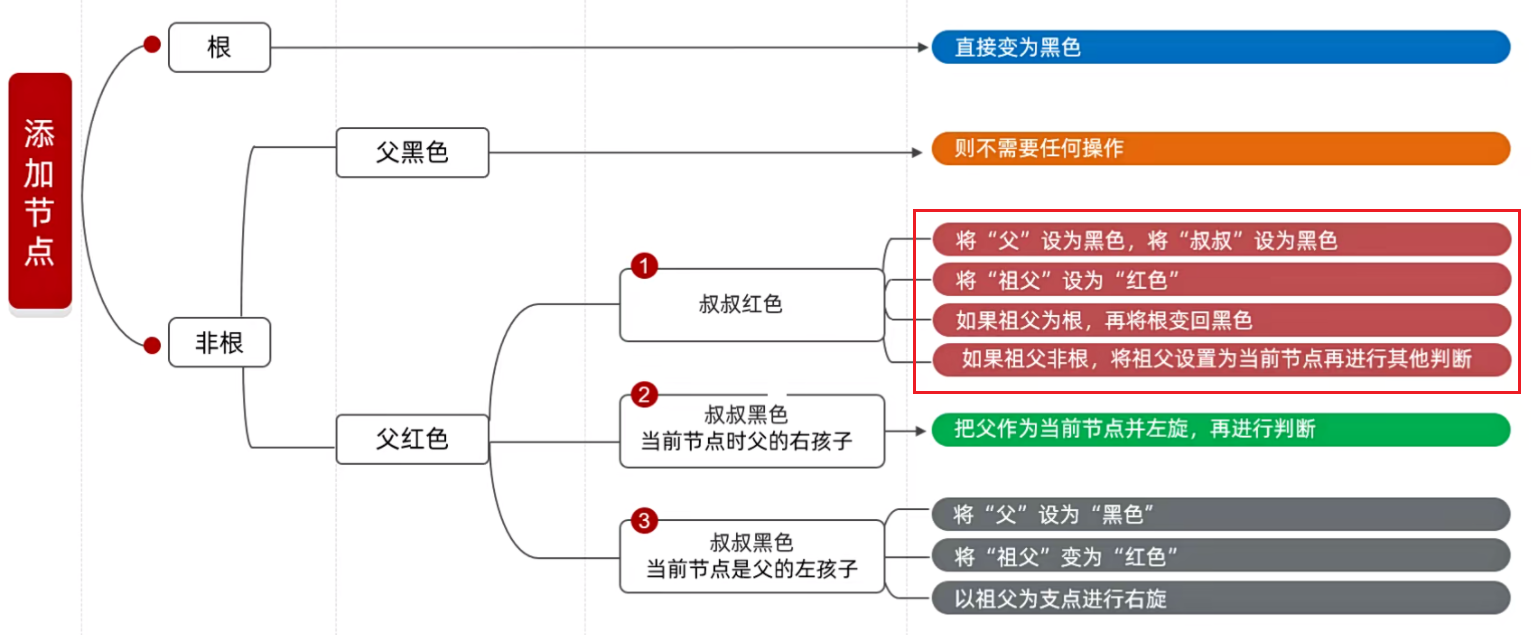
① 将 “父” 设置为黑色，将 “叔叔” 设置为黑色

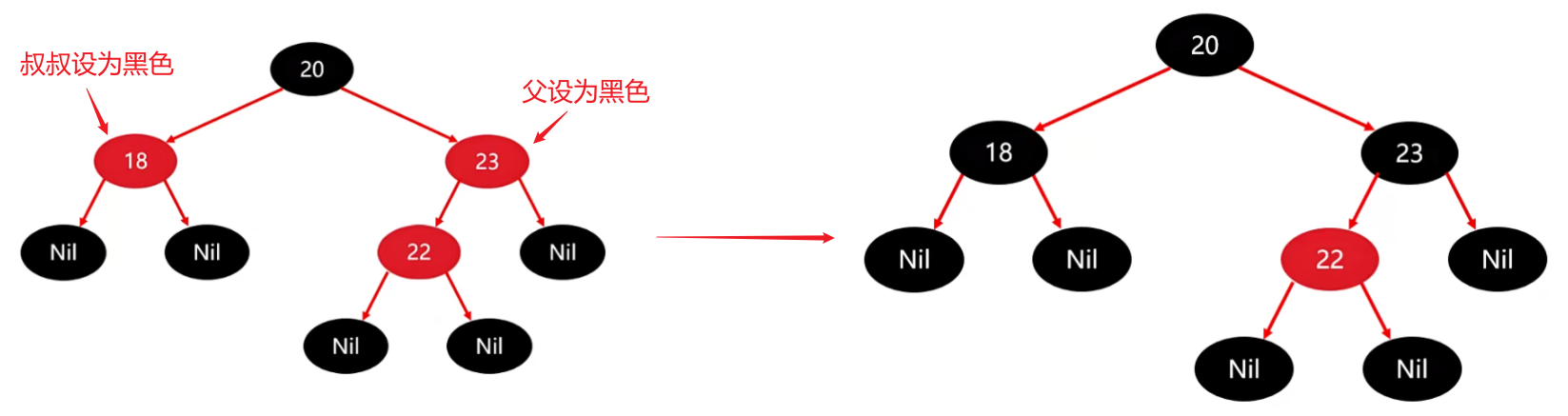
② 将 “祖父” 设为 “红色”

22 的祖父就是 20，因此需要将 20 变成红色。

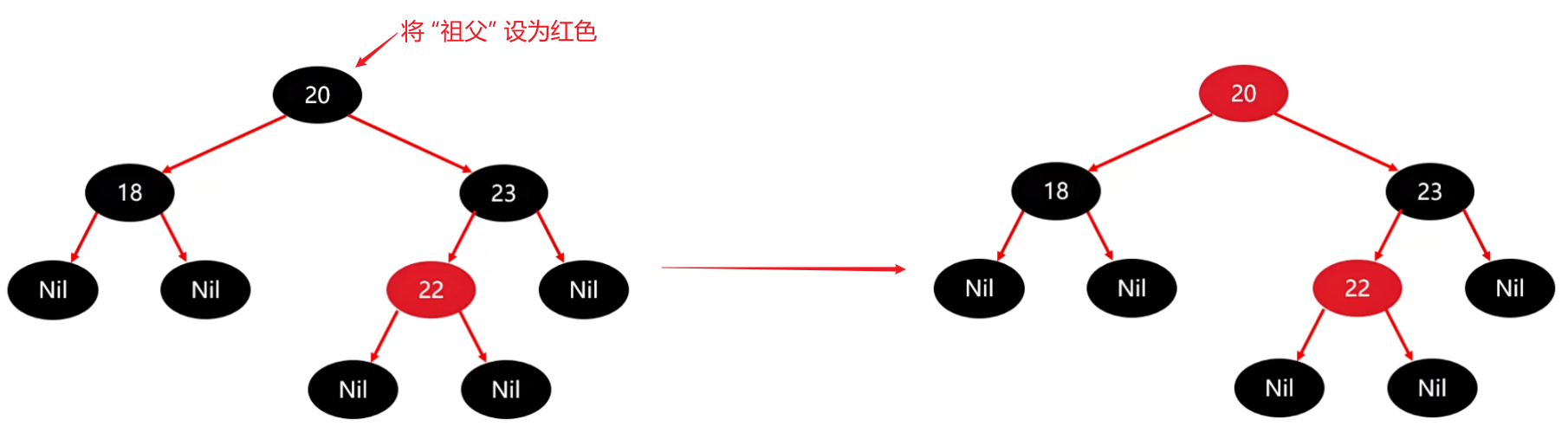
然后下面有两个相对立的。

③ 如果祖父为根，再将根变回黑色

由于此时祖父 20 是根，因此此时需要变回来。

---

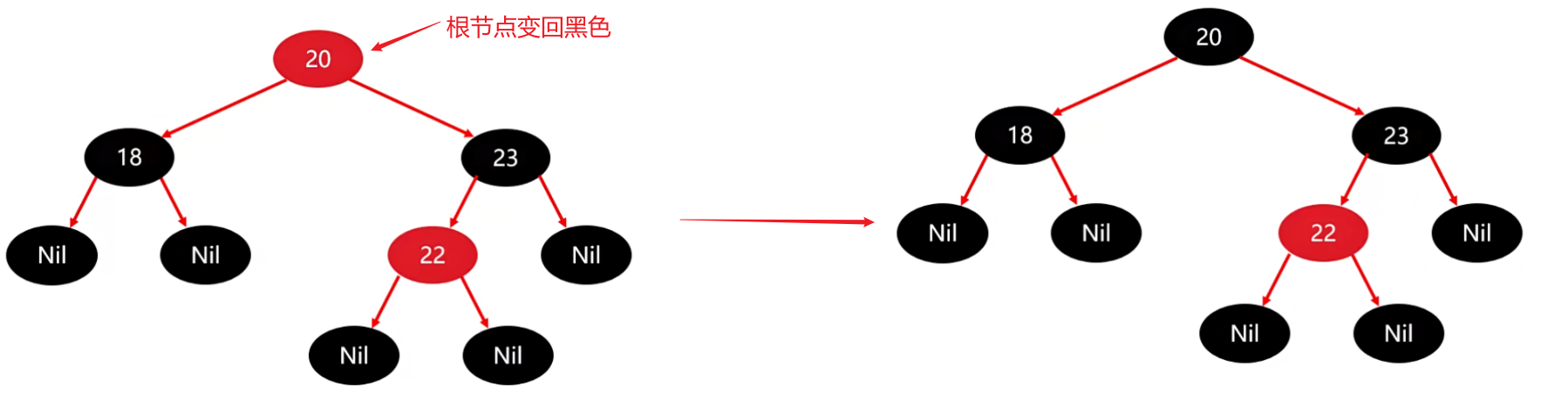
4）当前节点不为根节点，父节点为黑色

往下，添加 17节点，比了一下它发现，17 要比 20 小，所以应该存 20 的左边。

继续跟 18 节点比较，发现比 18 小，因此存 18 的左边，当做是 18 的左子节点。

再来对比一下规则，看看我们是否要来进行处理

如果我们添加的节点是非根，并且父节点是黑色，则不需要进行任何的操作。

因此 17 现在就放在这，不需要进行任何操作。

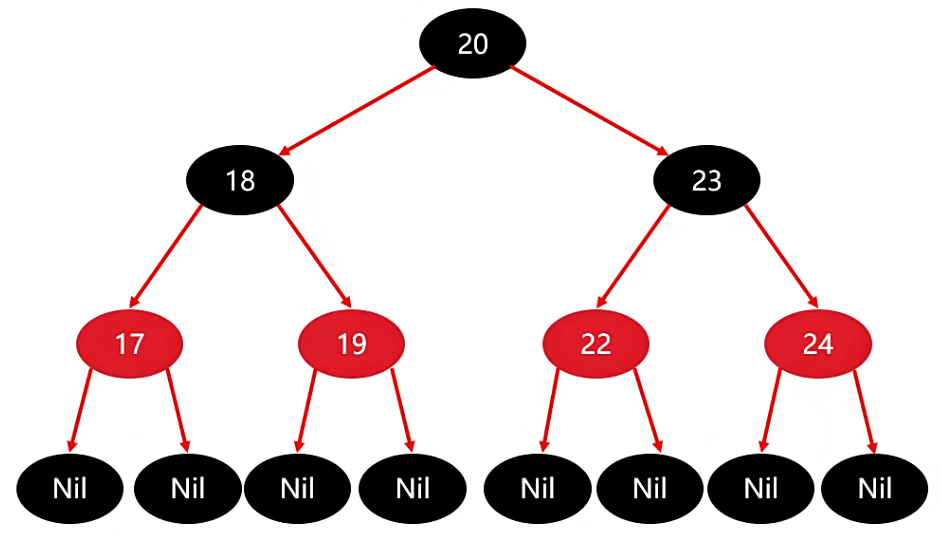
接下来是同样的道理，当我们添加 24 和 19 时，它们的父节点也都是黑色的，因此也不需要进行任何的调整。

----

当前节点不为根节点，父节点为红色，叔叔节点也为红色

接下来再来添加两个节点，添加这两个节点的时候就有点难了。

首先添加 15节点，结果对比，它应该是添加在 17节点 的左边。

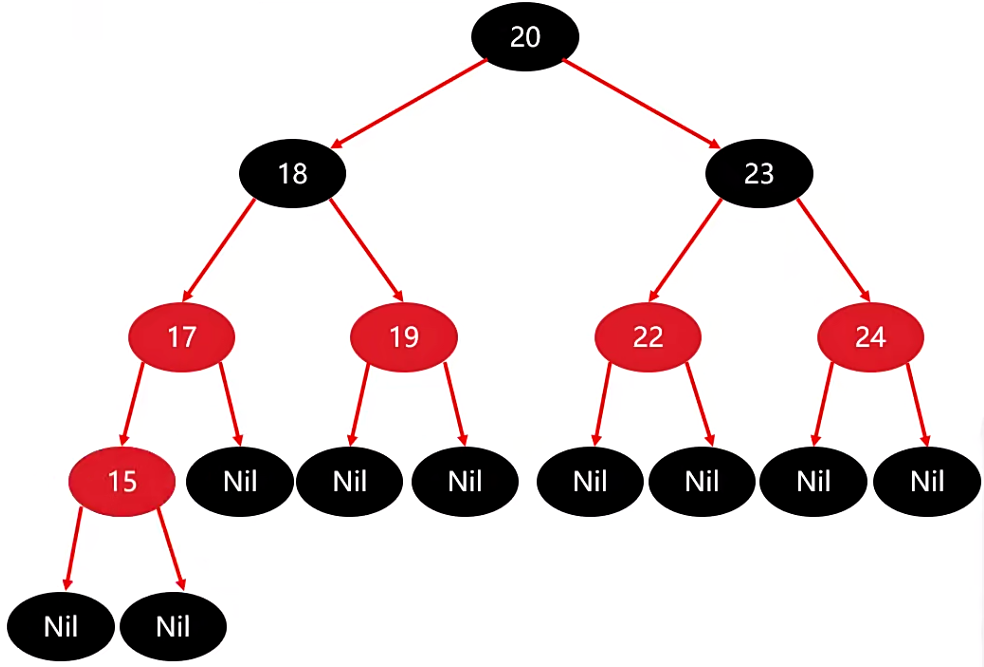
这个时候它的父节点是红色的，叔叔节点也是红色的，此时就需要使用到下面深红色的处理方案。

它需要将 父、叔、祖父... 都操作一下。

① 将 “父” 设置为黑色，将 “叔叔” 设置为黑色

② 将 “祖父” 设为 “红色”

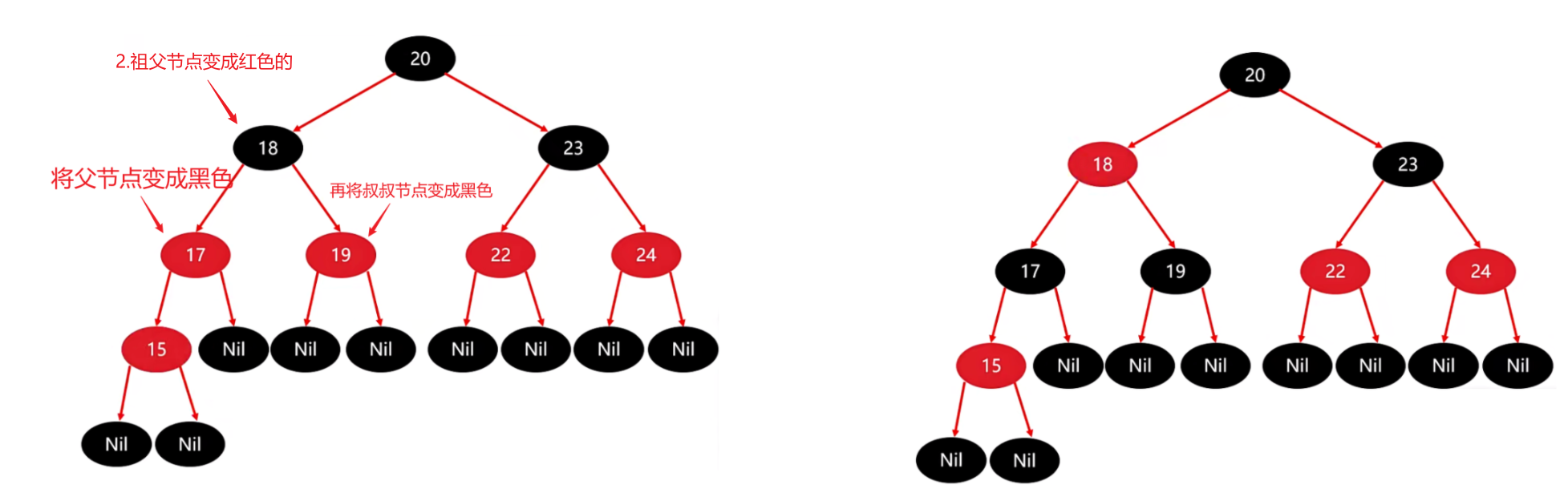
③ 如果祖父为非根，将祖父设置为当前节点再进行其他判断

此时祖父 18 不是根节点，所以此时我们要站在祖父节点的基础上，再次进行判断。

现在 18节点 的父节点是黑色的，此时我们需要再去表中找对应的处理方案。

可以看见，父节点是黑色的，不需要做任何操作，因此此时调整已经结束。

---

5）当前节点不为根节点，父节点为红色，叔叔节点为黑色，并且当且节点是父节点的左孩子

继续往下，添加 14节点，结果对比，14节点 应该放在 15 的左边，当做是 15节点 的左子节点。

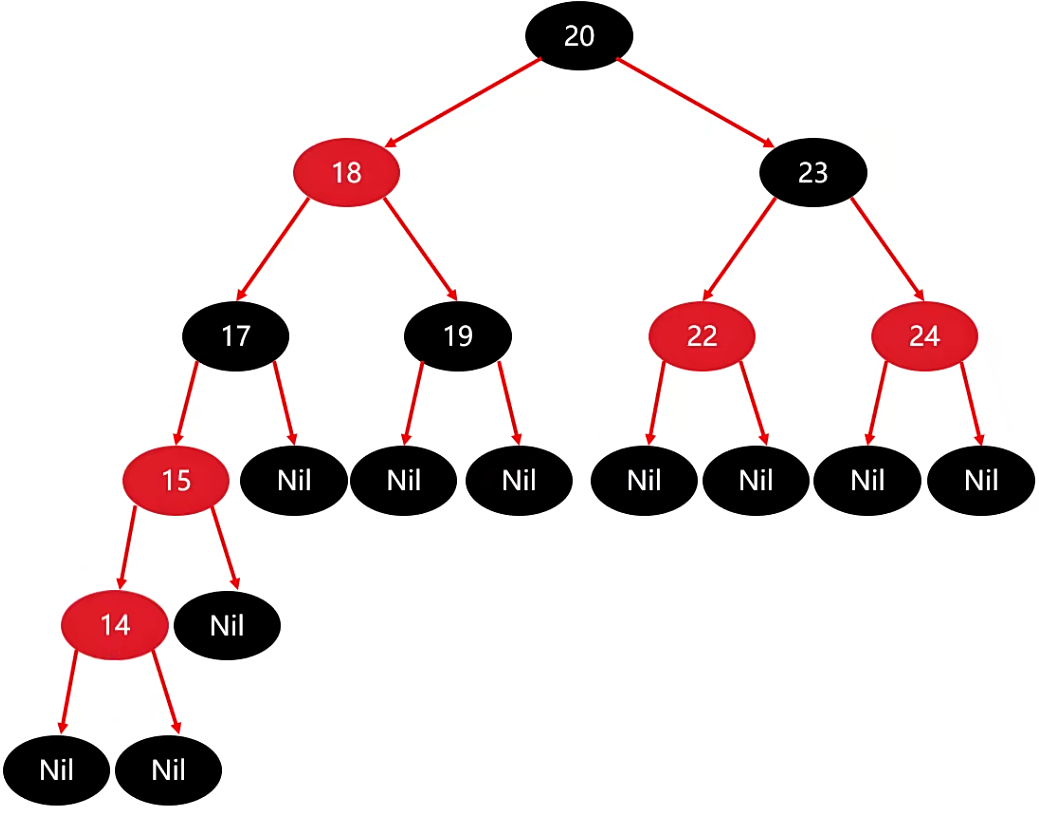
这个时候它其实也违背了红黑规则：不能出现两个红色相连的情况。

因此此时我们需要调整：14 的父节点是 红，叔叔节点是 Nil，即黑色，而且 14 是 15 的左子节点，因此要采取的是下面深灰色的处理方案。

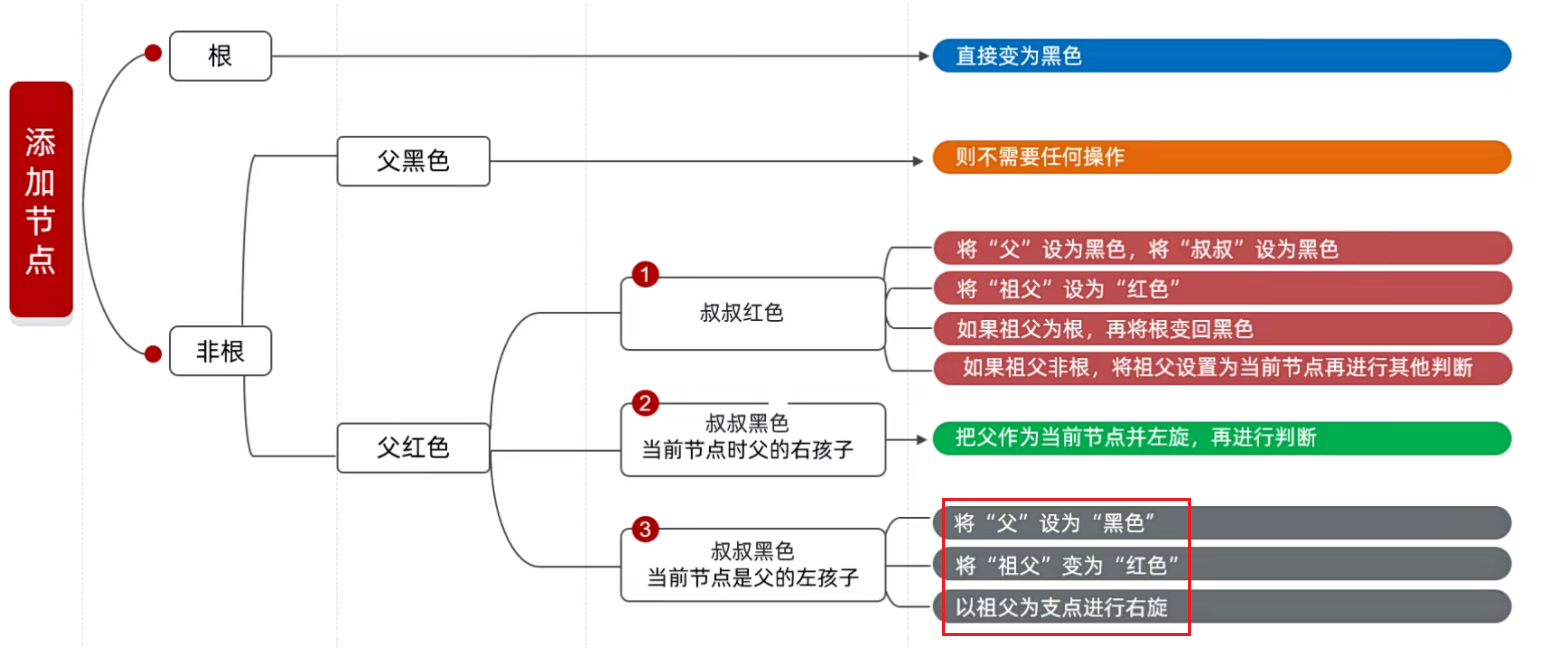
前两步如下图

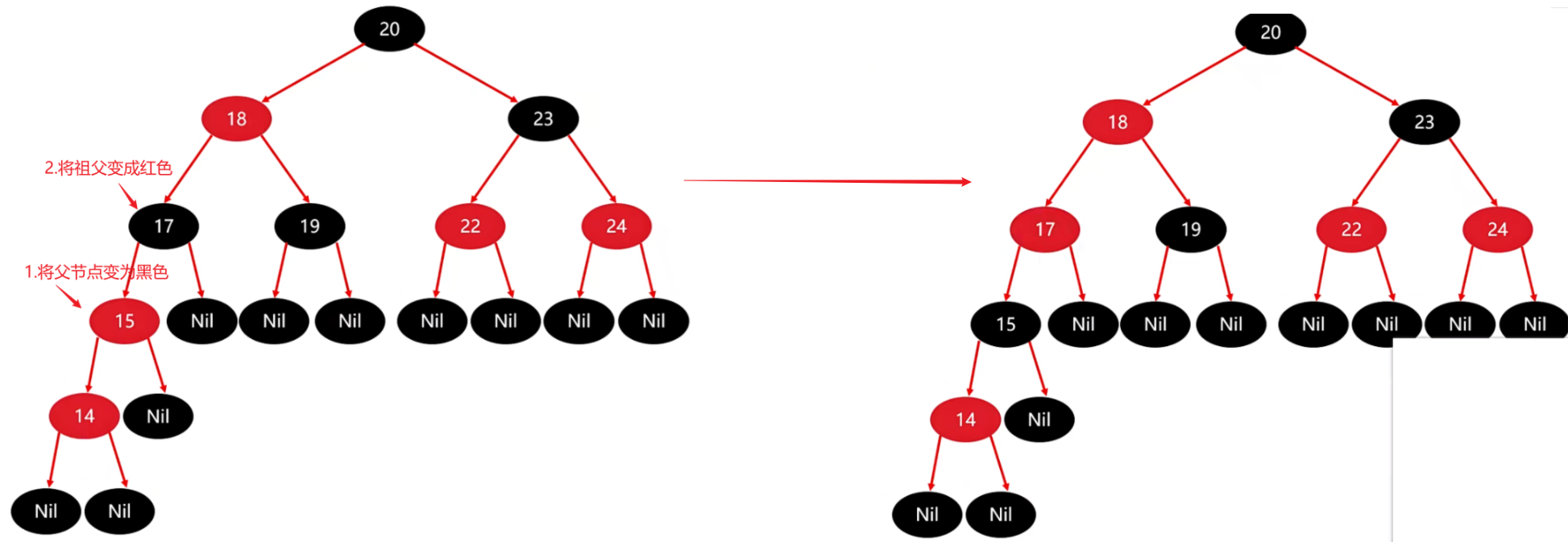
第三步：以祖父为支点进行右旋

在旋转的时候是不需要考虑 Nil 叶子结点的，直接转就行了，转完后再将叶子结点补上接口。

---

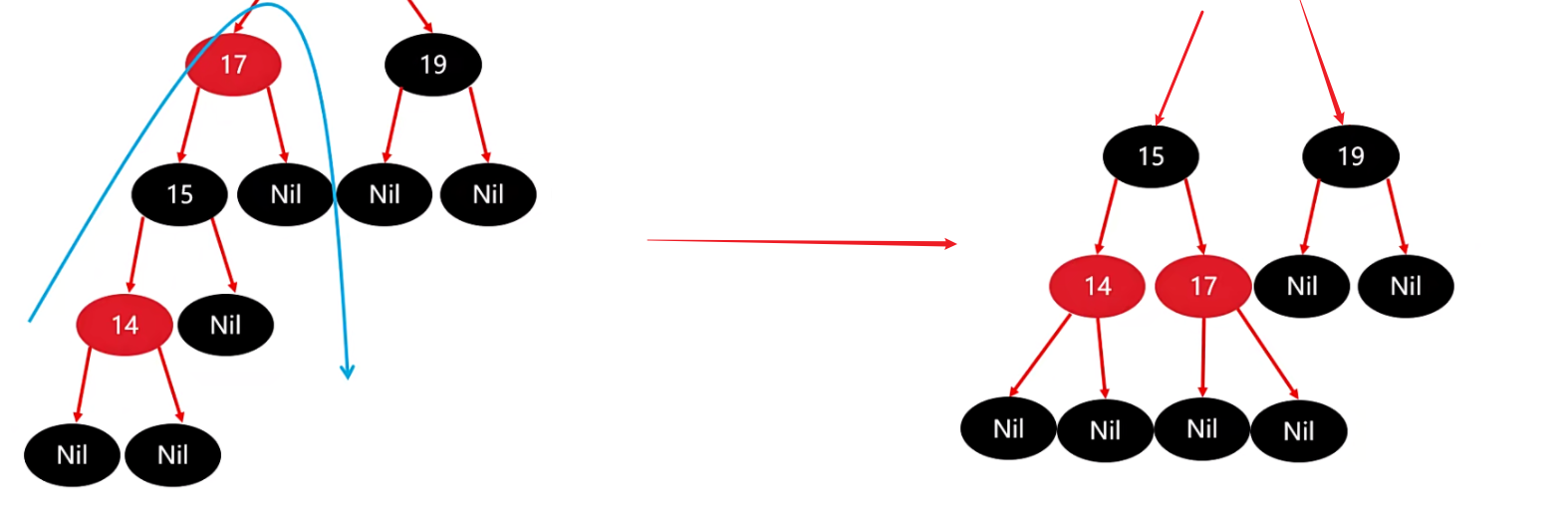
6）当前节点不为根节点，父节点为红色，叔叔节点为黑色，并且当且节点是父节点的右孩子

还有一种情况我们需要知道。

先将 14节点 去掉，假设我们刚刚添加的不是 14节点，而是 16节点。

由于 16节点 应该添加到 15节点 的右边，当做是 15 的右子节点。

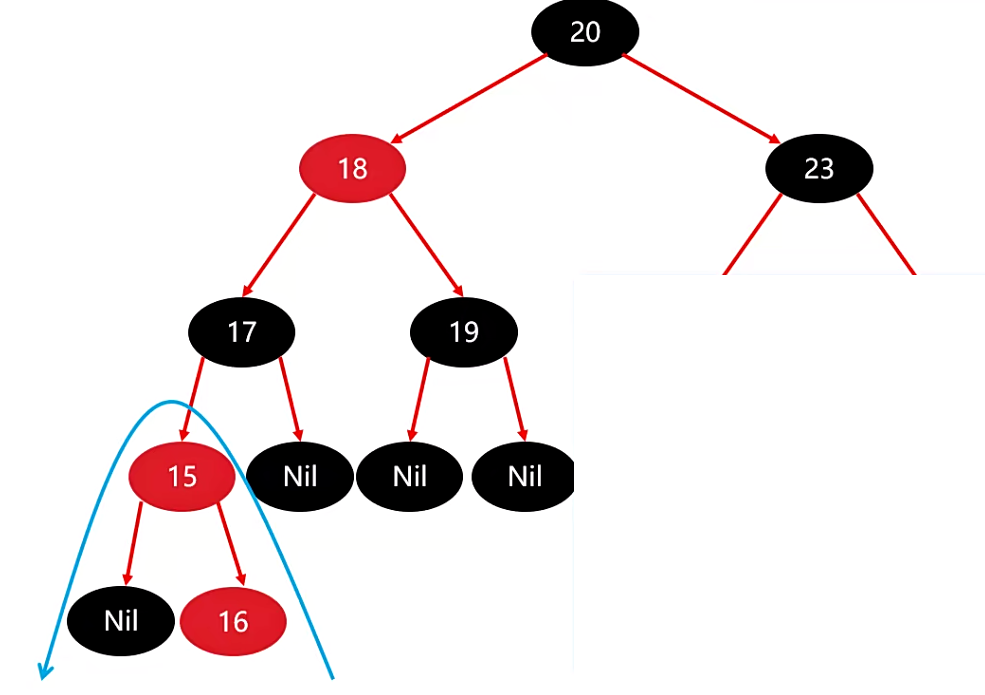
根据表中解决方案：16 的父 15 是红色的，它的叔叔是 15 旁边的 Nil，是黑色的，并且当前节点是父的右孩子，因此需要使用下面绿色的处理方案

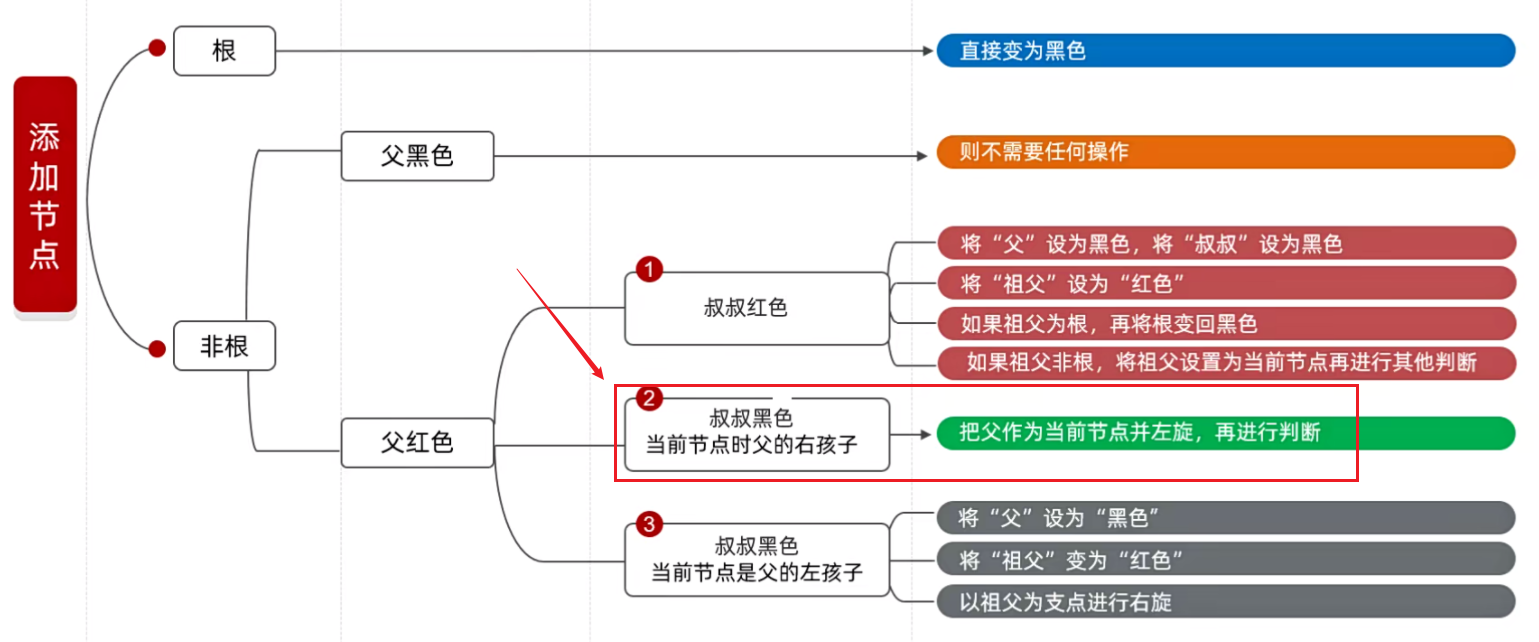
把父作为当前节点，并左旋，再进行判断

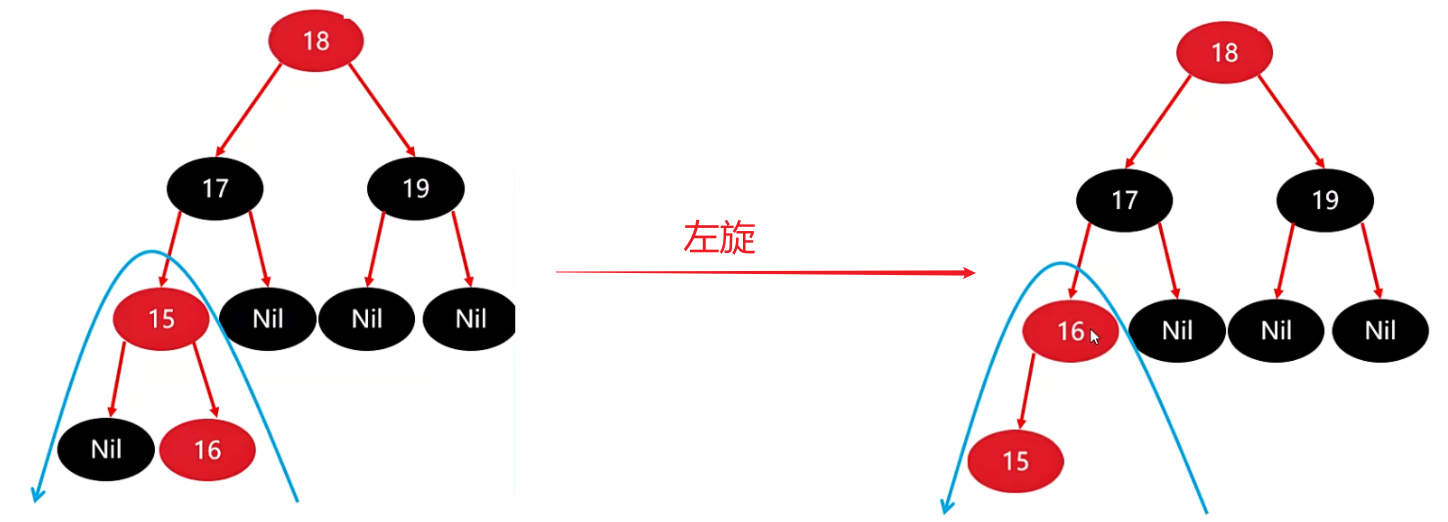
在判断的时候，我们需要站在 15 的基础上再来看问题了，因为在刚刚在调整的时候，它是将父节点作为当前节点。

15 的父节点是红色的，叔叔节点是黑色，而且 15 是 16 的左子节点，因此就需要采取下面深灰色的处理方案。

将父节点变成黑色，将组父节点变成红色。

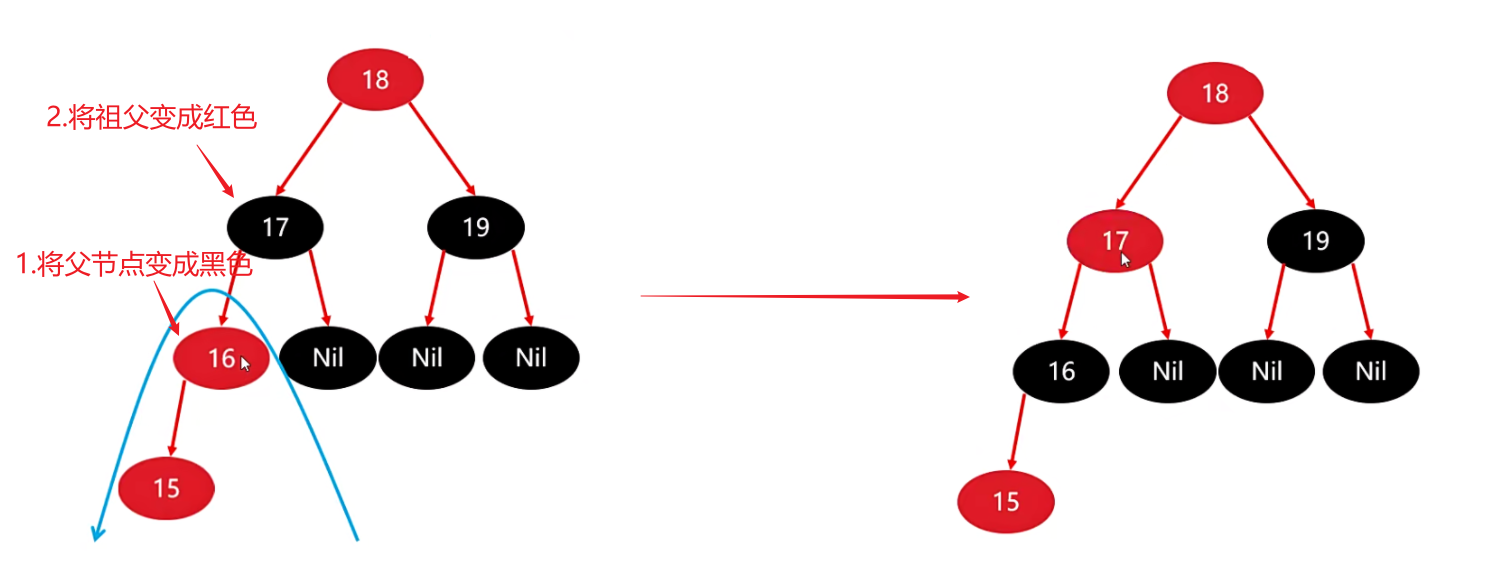
最后以祖父17为支点进行右旋。

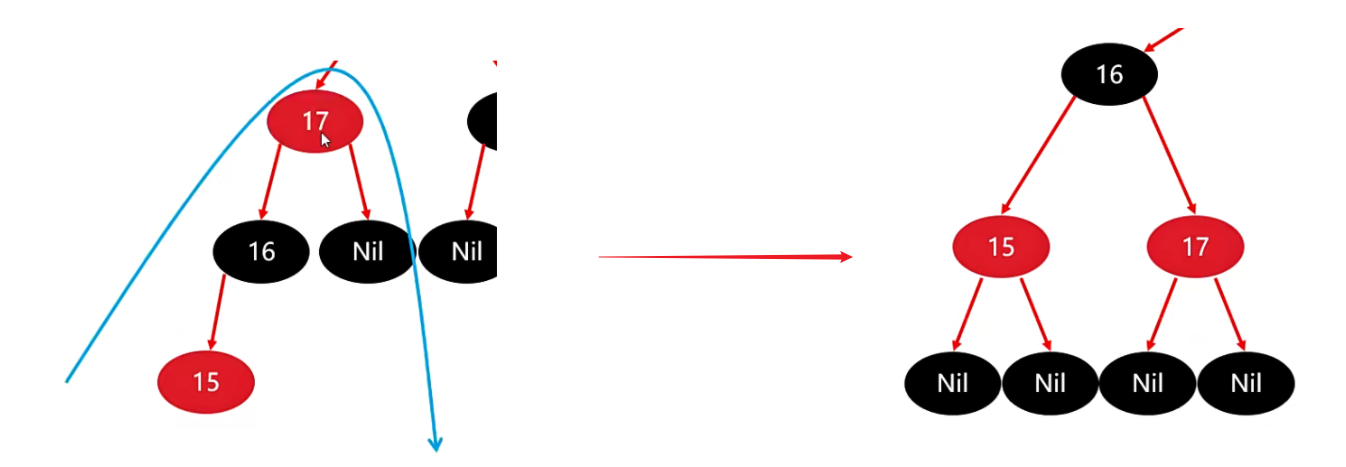
旋转完毕后，整棵树就变成了下面这种情况

---

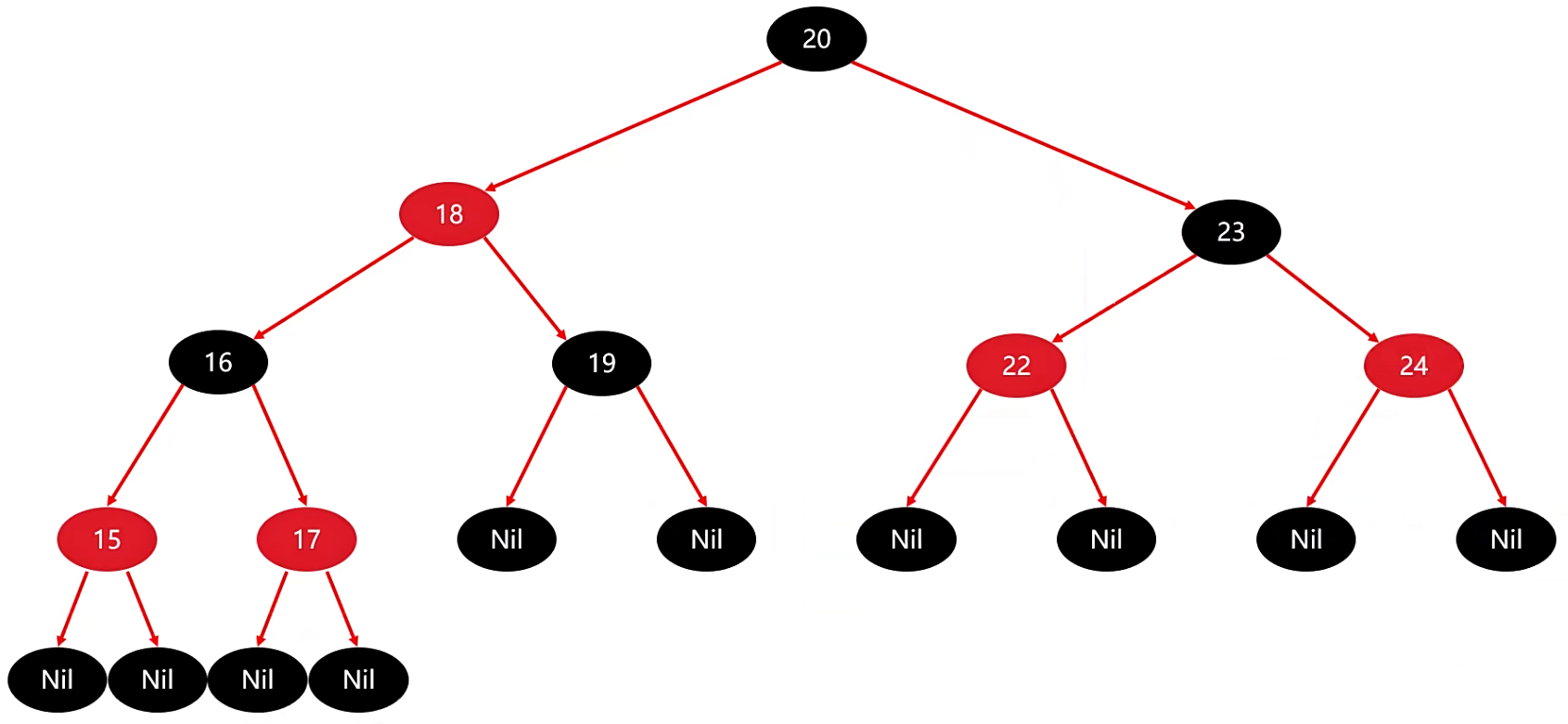
要注意的是，有两个地方需要 再进行其他判断，这一点一定要注意。

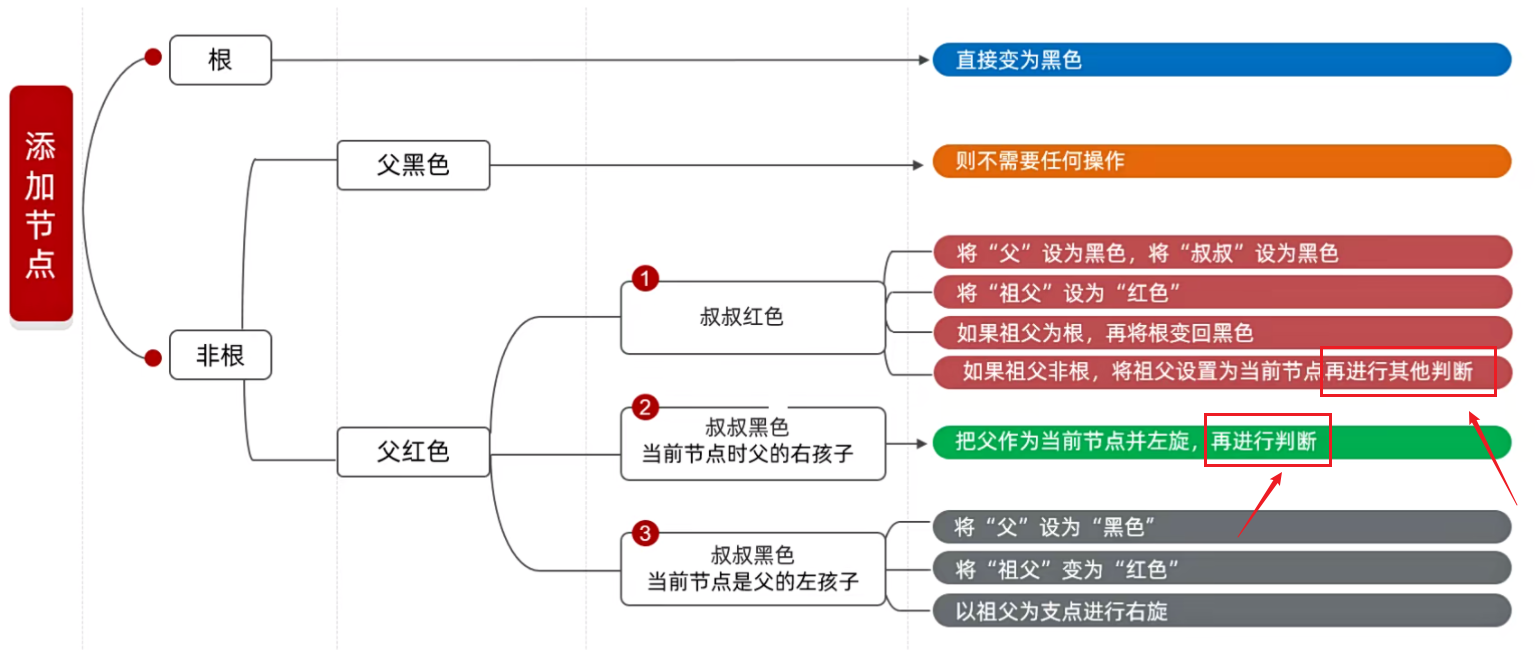
通过这两个情况知道了，有时候往红黑树中添加节点，不是调整一次就行了，有可能要调整两次，也有可能要调整三次，或者更多。

---

五、总结

红黑树增删改查的性能都很好。

但是有同学就觉得：处理方案这么多这么复杂，性能为什么还更好？

因为在这些处理方案中，真正浪费时间的其实是旋转，在红黑树中，更多的处理方案仅仅是修改颜色而已，修改颜色其实是不浪费时间的，它改变的仅仅是变量中记录的值而已。

并且在这些处理方案中，并不是每次都需要进行旋转的，旋转的次数跟平衡二叉树比，要少太多了，因此红黑树增删改查的性能都很好。