机器学习-白板推导-系列（四）笔记：感知机/Fisher判别/判别模型(逻辑回归)/生成模型(高斯判别/朴素贝叶斯)

---

0 笔记说明

来源于【机器学习】【白板推导系列】【合集 1～23】，我在学习时会跟着up主一起在纸上推导，博客内容为对笔记的二次书面整理，根据自身学习需要，我可能会增加必要内容。

注意：本笔记主要是为了方便自己日后复习学习，而且确实是本人亲手一个字一个公式手打，如果遇到复杂公式，由于未学习LaTeX，我会上传手写图片代替（手机相机可能会拍的不太清楚，但是我会尽可能使内容完整可见），因此我将博客标记为【原创】，若您觉得不妥可以私信我，我会根据您的回复判断是否将博客设置为仅自己可见或其他，谢谢！

本博客为（系列四）的笔记，对应的视频是：【(系列四) 线性分类1-背景】、【(系列四) 线性分类2-感知机（Perceptron）】、【(系列四) 线性分类3-线性判别分析（Fisher）-模型定义】、【(系列四) 线性分类4-线性判别分析（Fisher）-模型求解】、【(系列四) 线性分类5-逻辑回归（Logistic Regression）】、【(系列四) 线性分类6-高斯判别分析（Gaussian Discriminant Analysis）-模型定义】、【(系列四) 线性分类7-高斯判别分析（Gaussian Discriminant Analysis）-模型求解（求期望）】、【(系列四) 线性分类8-高斯判别分析（Gaussian Discriminant Analysis）-模型求解（求协方差）】、【(系列四) 线性分类9-朴素贝叶斯分类器（Naive Bayes Classifer）】。

下面开始即为正文。

---

1 背景

什么是线性？

两个变量之间存在一次方函数关系，就称它们之间存在线性关系。通俗一点讲，如果把这两个变量分别作为点的横坐标与纵坐标，其图象是平面上的一条直线，则这两个变量之间的关系就是线性关系。

先来看看线性回归模型f(x)=w^Tx+b的特点：

（1）线性：f(x)关于x（即p维特征）是线性的，关于w（参数）也是线性的；

（2）全局性：线性回归模型的参数即w和b是针对所有数据的，并没有分割数据然后对各个数据片段分别做线性回归；

（3）数据未加工：线性回归模型只是对数据线性组合后直接将结果输出，并没有对数据进行处理（如降维等）。

线性回归模型是比较简单的模型，如果对上述三个特点进行更改的话，就可以演变为其他的模型，如：

（1）特征转换（多项式回归）中，关于x就是非线性的，因为存在x的高次项；

（2）感知机与神经网络中，关于参数w是非线性的，这里的非线性是指w会不断变化；

（3）线性分类将线性回归的结果w^Tx+b作为输入，通过激活函数δ后输出，即δ(w^Tx+b)；

（4）样条回归将输入空间即所有x_i进行分割，之后对每个数据段分别进行线性回归。

下面着重讨论线性分类问题。

线性回归加上激活函数和降维就是线性分类。 设激活函数为f，y=f(w^Tx+b)，输出y有两种形式：

（1）y∈{0,1}，称为硬分类问题，y只有两个值0或者1。包括感知机（下面第二节）、线性判别分析（下面第三节）等；

（2）y∈[0,1]，称为软分类问题，y为概率值，取区间[0,1]之间的数。有两种——【判别方法/模型：如逻辑回归（下面第四节）】和【生成方法/模型：如高斯判别分析（下面第五节）与朴素贝叶斯分类器（下面第六节）】。

将f的逆f^-1称为link函数。举个栗子，f将【w^Tx+b】映射到【{0,1}】，f^-1将【{0,1}】映射到【w^Tx+b】。

监督学习方法分为生成方法与判别方法，所对应生成的模型分别称为生成模型与判别模型。下面看看生成方法与判别方法及之间的区别。

1.1 生成方法

生成方法由数据学习联合概率分布P(X,Y)，然后求出条件概率分布P(Y|X)作为预测的模型，即生成模型：P(Y|X)=P(X,Y)/P(X)。称为生成方法是因为模型表示了给定输入X产生输出Y的生成关系。

生成方法的特点：生成方法可以还原出联合概率分布P(X,Y)，而判别方法则不能；生成方法的学习收敛速度更快，即当样本容量增加的时候，学到的模型可以更快地收敛于真实模型；当存在隐变量时，仍可以用生成方法学习，此时判别方法就不能用。

1.2 判别方法

判别方法由数据直接学习决策函数f(X)或者条件概率分布(即P(Y|X))作为预测的模型，即判别模型。判别方法关心的是对给定的输入X，应该预测什么样的输出Y。

判别方法的特点：判别方法直接学习的是条件概率P(Y|X)或决策函数f(X)，直接面对预测，往往学习的准确率更高；由于直接学习P(Y|X)或f(X)，可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习问题。

1.3 四种概率分布

1.3.1 伯努利分布

若随机变量X服从参数为p的伯努利分布（Bernoulli Distribution），且X只取0或1，则有：【P(X=1)=p】和【P(X=0)=1-p】。

1.3.2 二项分布

若随机变量X服从参数为n、p的二项分布（Binomial Distribution），即X～B(n,p)，则有：【P(X=k)=C_n^k·p^k·(1-p)^n-k，其中k∈[0,n]】。

1.3.3 类别分布

若随机变量X服从类别分布（Categorical Distribution），即X～Cat(α₁,α₂,…α_k)，其中Σα_i=1，则有：【P(X=i)=α_i，j∈[1,k]】。

1.3.4 多项分布

若随机向量X=(X₁,X₂,…,X_n)满足：① X_i≥0，且ΣX_i=N；② 设m_i为任意非负整数，且Σm_i=N。则事件{X₁=m₁,X₂=m₂,…,X_n=m_n}的概率为：

则称随机向量X=(X₁,X₂,…,X_n)服从多项分布，记作X～PN(N:p₁,p₂,…,p_n)。

---

2 感知机

感知机是一种二分类的线性模型，是使用错误驱动的一种方法，感知机的模型为f(x)=sign(w^Tx)，其中x与w均是p维向量，即x∈R^p，w∈R^p，sign(a)为符号函数，a≥0时为+1，a＜0为-1。

数据集为{(x_i,y_i)}，i=1…N。假定数据集是线性可分的，设刚开始w=w₀∈R^p，如下图：

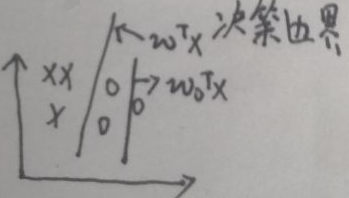
有两种数据，分别用×和o表示，图中的w^Tx为最终的决策边界，刚开始决策边界为w₀^Tx，可以看出分类效果并不理想。感知机的策略即损失函数为：

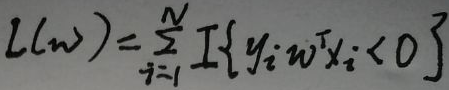
下面对损失函数解释：首先f(x)=sign(w^Tx)，所以【当w^Tx_i＞0时，y_i=+1；当w^Tx_i＜0时，y_i=-1】，那【y_iw^Tx_i＞0】，这是模型正确分好的，则模型分错的时候【y_iw^Tx_i＜0】。然后看看上图，损失函数L(w)的值为模型分错的样本个数，I函数是这样计算的——【y_iw^Tx_i＞0时I为0；y_iw^Tx_i＜0时I为1】。但是上图的L(w)的一个缺点是不可导。下面是新的L(w)：

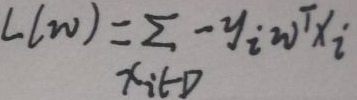
D为错分的样本集，上面的L(w)是可导的，对L(w)求导得：

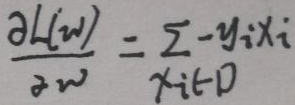
记上面的偏导数为▽_wl，感知机使用随机梯度下降法（stochastic gradient descent,SGD），调整每一步的参数w——【w^(t+1)=w^(t)+λ▽_wl】，λ为学习率。过程是这样的——先给定一个w⁽⁰⁾，根据学习率λ慢慢调整w，结束条件为【到达迭代次数】或【达到一定阈值】。

---

3 线性判别分析

线性判别分析(linear discriminant analysis，LDA)是由Fisher提出的。

3.1 模型定义

数据集D中有N个样本实例，D = {(x₁, y₁), (x₂, y₂),…,(x_N, y_N)}。现在构造两个矩阵X与Y：X = (x₁,x₂,…,x_N)^T，每个样本的x_i∈R^p，i=1…N，X为N*P阶矩阵；Y=(y₁,y₂,…,y_N)^T，每个样本的y_i∈R，i=1…N，且y_i只取{C₁=+1,C₂=-1}中的一个值，Y为N*1阶矩阵。

根据y_i的值可以将X分为两类：① C₁：X_a={对应的x_i|y_i=+1}，共有|X_a|=N₁个样本；② C₂：X_b={对应的x_i|y_i=-1}，共有|X_b|=N₂个样本。样本总数N=N₁+N₂。

线性判别分析LDA的方法是降维——将p维数据x_i投影到一个合适的1维坐标轴w上（w就是之前的参数w，w是一个p维向量），使得数据x_i的投影z_i具有【同类的数据方差足够小、足够紧凑】和【不同类间的数据距离足够大】，之后选择一个合适的阈值b，然后将X划分为两类：【大于b的z_i对应的x_i】和【小于b的z_i对应的x_i】。示例如下：

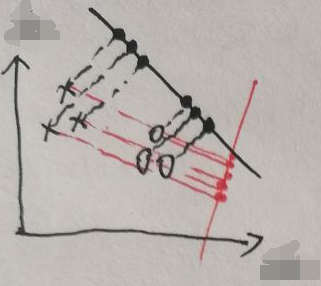
上图假设每个x_i的p=2，即维度为2，分别为横纵坐标轴，假设N=6，即共有6个样本，有两类数据分别用o和×表示。这些数据被投影到红黑两条一维坐标轴上，可以看出：【黑轴上，同类数据足够紧凑，不同类间的数据距离足够大】和【红轴上，不同类的数据杂乱地混在一起，难以区分】。因此黑轴的效果比红轴的效果好。

对任意一个样本x_i，在w轴上的投影是多少呢？请看下图：

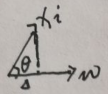
假设x_i的投影是z_i，记Δ=z_i，设x_i与Δ的夹角为θ，限定||w||=1，则有【Δ=|x_i|·cosθ】。而向量x_i与向量w的内积为【x_i·w=w^Tx_i=|x_i|·|w|cosθ=|x_i|·cosθ=Δ】。综上，x_i的投影z_i=Δ=w^Tx_i，下面求投影z_i的均值与协方差矩阵：

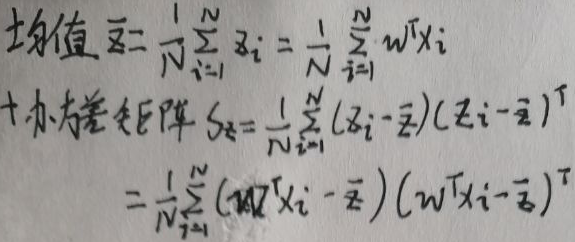
根据本节【1.1 模型定义】的第二段描述，将X分为两类——【C₁】和【C₂】，则可写出它们的投影的均值与协方差矩阵：

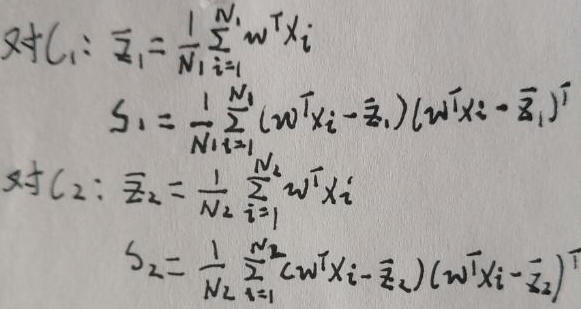
规定目标函数J(w)为：

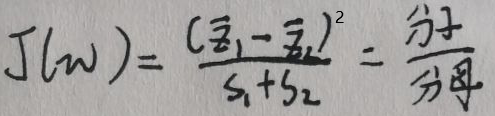
先对分子分母进行化简，最后求出J(w)：

目标函数J(w)由上图最后一行给出。下面求解模型的参数w。

3.2 模型求解

定义【between-class类间方差S_b】和【within-class类内方差S_w】为：

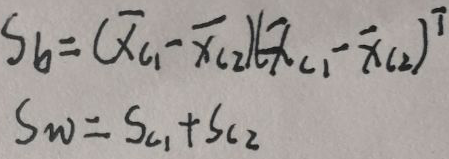
则目标函数J(w)为（还是比较好看的哈）：

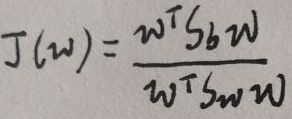
还是用极大似然估计MLE：

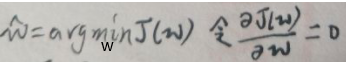
对J(w)求导：

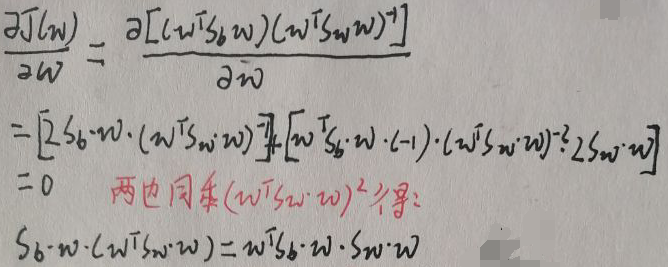
上图最后一行中，w是p×1的向量，w^T是1×p的向量，S_w=S_c1+S_c2，而S_c1和S_c2是协方差矩阵，均为p×p维矩阵（不信自己去推），S_b也是p×p维矩阵。所以S_b·w·(w^T·S_w·w)=w^T·S_b·w·S_w·w中，【w^T·S_w·w】和【w^T·S_b·w】均为1×1的正实数（首先两个都是二次型，中间的协方差矩阵S_b与S_w为对称非负定矩阵，这是百度百科上写的，所以两个二次型均≥0），所以：

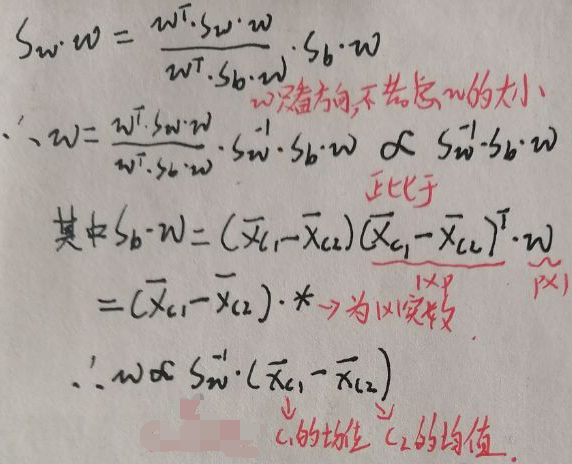
上图中S_w为：

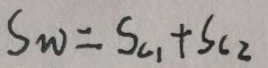
因为只关心投影方向，不关心w大小，所以最终得到的w的方向与S_w^-1·(x’_c1+x’_c2)的方向相同（不会打上面的一杠，所以用撇’代替咯）。

求解完成。

---

4 逻辑回归

逻辑回归是一种概率判别模型，直接对P(Y|X)进行建模，之后通过MLE求解参数w。先看下图的sigmoid函数：

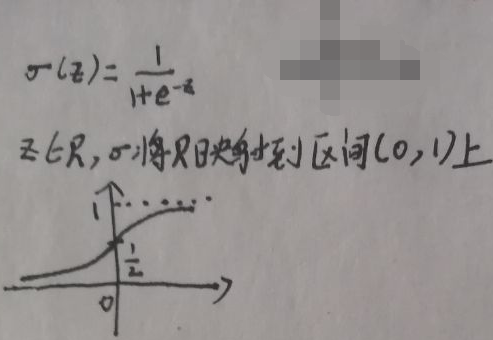
逻辑回归中，将w^Tx正好映射到概率p，p∈(0,1)。下面考虑的是二分类问题，即y_i∈{0,1}。注意概率判别模型输出的是概率值大小。首先规定p₀与p₁如下：

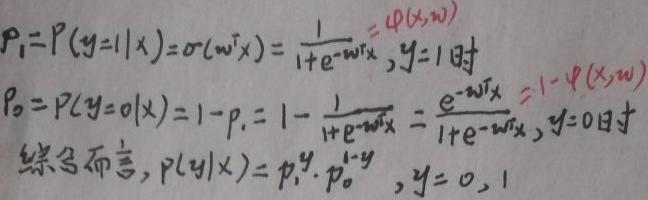
似然函数P(Y|X)为：

最后一行框住的表达式（up主说是交叉熵，我并不了解这些知识）中两个x应该是x_i，先记为L(w)，下面会进行修改，然后继续化简：

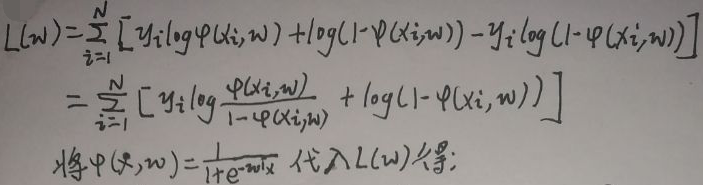
接着上图（真费劲）：

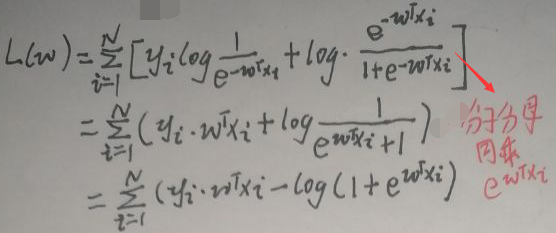
对L(w)关于w求导（注意y_i为实数，且只取0或1；将log视为ln函数）：

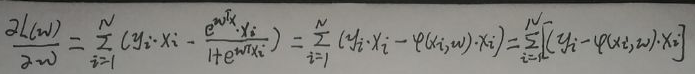
令导数=0，得到w的估计值即为所求：

这样得到的逻辑回归模型在预测新数据x_i时，先代入两个式子，得到的概率值如果左面大，就定为【Y=1】一类，如果右面大，就定为【Y=0】一类。

但是导数为0时w的估计值好像比较难求，反正我放弃了。下面用随机梯度下降法（stochastic gradient descent,SGD），调整每一步的参数w——【w^(t+1)=w^(t)+λ▽_w】，λ为学习率，▽_w等于上面倒数第二张图的导数。过程是这样的——先给定一个w⁽⁰⁾，根据学习率λ慢慢调整w，结束条件为【到达迭代次数】或【达到一定阈值】。

---

5 高斯判别分析

数据集D中有N个样本实例，D = {(x₁, y₁), (x₂, y₂),…,(x_N, y_N)}。每个样本的x_i∈R^p，i=1…N；每个样本的y_i∈R，i=1…N，且y_i只取0或1。

根据y_i的值可以将数据集D分为两类：① C₁：{(x_i, y_i)|y_i=1,对应的x_i}，假设共有N₁个样本；② C₂：{(x_i, y_i)|y_i=0,对应的x_i}，假设共有N₂个样本。样本总数N=N₁+N₂。

贝叶斯定理为：P(y|x)=(P(x|y)·P(y))/P(x)。高斯判别分析是一种生成模型，生成模型关心的不是【P(y=0|x)与P(y=1|x)】的大小，而是仅关心二者的大小关系即哪个更大一些。因为输入数据X = (x₁,x₂,…,x_N)^T已知，所以贝叶斯定理的分母即P(x)是已知的且为可以算出的常数，而且P(x)与y无关，所以P(y|x)∝(P(x|y)·P(y))，其中【P(y)是先验，P(x|y)为似然，P(y|x)为后验】。高斯判别分析是对P(x|y)·P(y)即P(x,y)建模：

现在真正开始高斯判别分析的讨论。

5.1 模型定义

高斯判别分析假设条件概率服从高斯分布——【x|y=1～N(μ₁,ε)】和【x|y=0～N(μ₂,ε)】，即二者服从均值不同但方差相同的高斯分布，可以简写为x|y～[N(μ₁,ε)]^y[N(μ₂,ε)]^1-y，y=1或0。下面定义对数log似然函数：

显然上面L(θ)中的参数θ=(μ₁,μ₂,ε,φ)，下面求解这四个参数。

5.2 模型求解

首先将上图的L(θ)再稍微化简下：

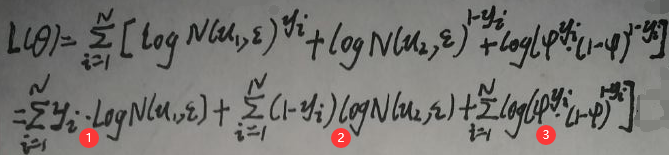
将L(θ)划分为三部分，标号为1、2、3式。

5.2.1 φ的求解

只有3式与φ有关，所以对其进行求导即可，记3式为L(φ)，对其化简及求导如下：

即φ=N₁/N。

5.2.2 μ₁与μ₂的求解

只有1式与μ₁有关，所以对其进行求导即可，记1式为L(μ₁)，对其化简（p为x_i的维度）如下：

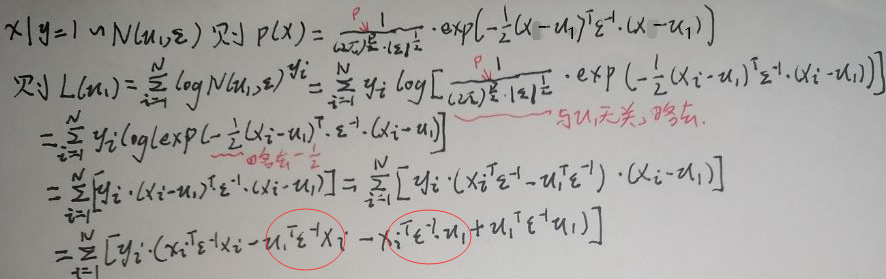
上图最后一行圈住的两个式子中，μ₁是p×1的，ε是p×p的，x_i是p×1的，所以两个式子均为1×p×p×p×p×1=1×1的实数，实数的转置还是自己，因此二者相同，接着再化简及求导：

μ₁由上图最后一行给出。下面求μ₂。

只有2式与μ₂有关，所以对其进行求导即可，记2式为L(μ₂)，对其化简（p为x_i的维度）如下：

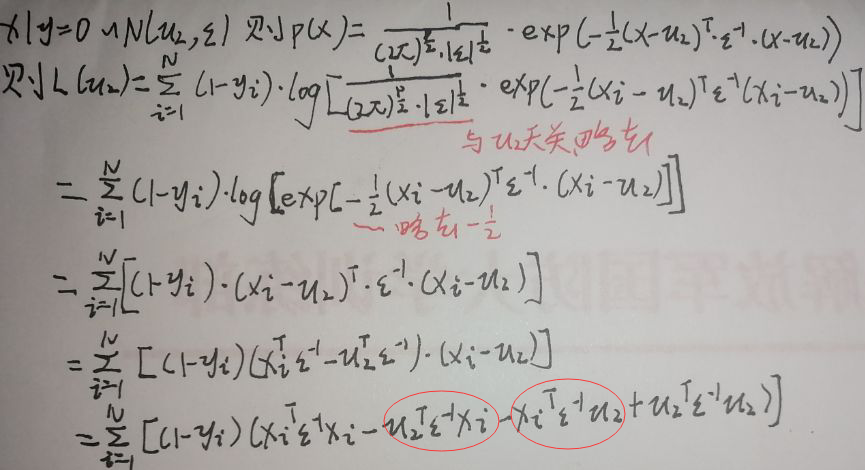
上图最后一行圈住的两个式子中，μ₂是p×1的，ε是p×p的，x_i是p×1的，所以两个式子均为1×p×p×p×p×1=1×1的实数，实数的转置还是自己，因此二者相同，接着再化简及求导：

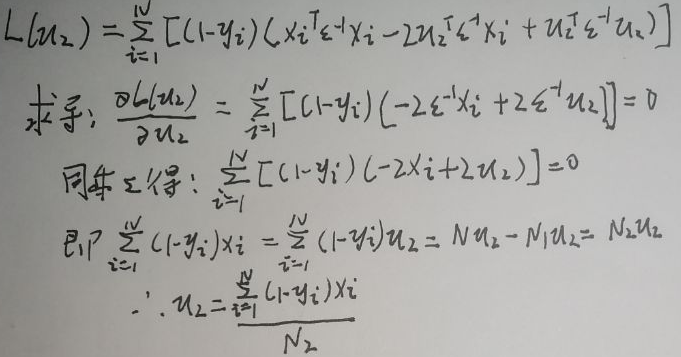
μ₂由上图最后一行给出。

5.2.3 ε的求解

只有1、2式与ε有关，所以对其进行求导即可，记1+2式为L(ε)，对其化简（p为x_i的维度）如下：

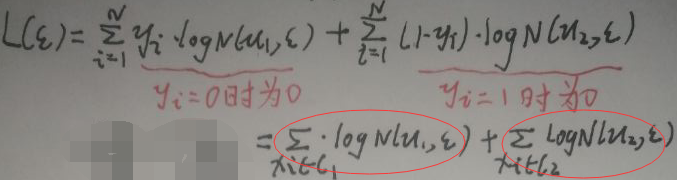
上图最后一行圈住的两个式子中，先求左面的，之后根据对称性得出右面的：

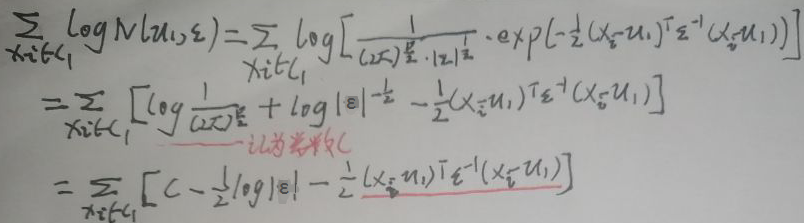
上图最后一行划线的式子中，μ₁是p×1的，ε是p×p的，x_i是p×1的，所以两个式子均为1×p×p×p×p×1=1×1的实数，实数的迹tr还是自己，【一个n×n矩阵A的主对角线上各个元素的总和被称为矩阵A的迹，记作tr(A)】。先引入几个关于迹及迹求导的公式（A、B、C均为n×n的矩阵）：

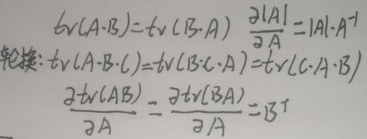
因为划线的式子为实数，且实数=tr(实数)，所以直接【将划线的式子作为tr(划线的式子)】，接着再化简：

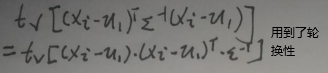
没忘吧，本节【5.2.3 ε的求解】中第一张图片的圈住的两个式子中，左面的式子还没化简完，继续化简：

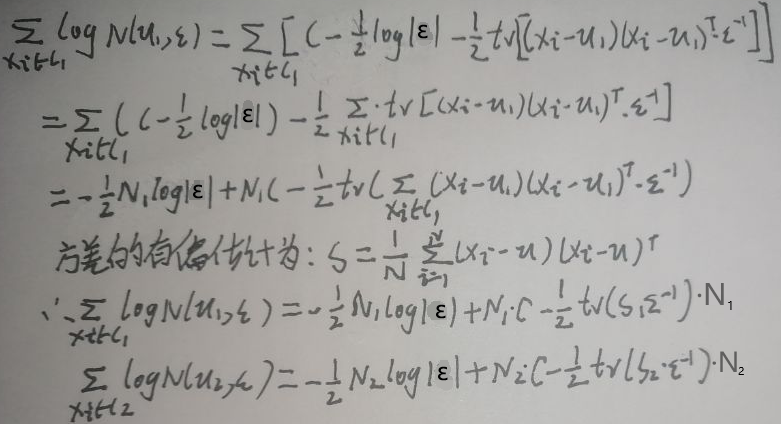
上图最后两行给出本节第一张图片的圈住的两个式子的化简形式（注意区分常数C与括号，我可能写的有点难以辨认），则L(ε)为：

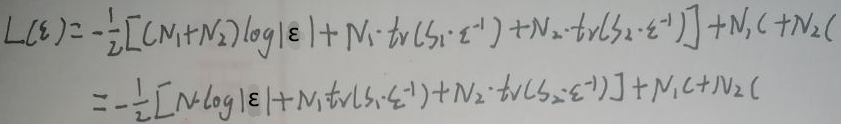
根据轮换性，tr(S₁·ε^-1)=tr(ε^-1·S₁)，tr(S₂·ε^-1)=tr(ε^-1·S₂)。则L(ε)为：

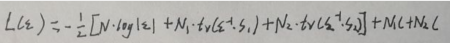
对L(ε)求导并令导数=0：

由最后一行可得：ε=(N₁·S₁+N₂·S₂)/N。

5.3 总结

（1）φ=N₁/N。N为样本总数，N1为【y_i=1对应的x_i的总个数】；

（2）μ₁=∑y_i·x_i/N₁；μ₂=∑(1-y_i)·x_i/N₂。N2为【y_i=0对应的x_i的总个数】；

（3）ε=(N₁·S₁+N₂·S₂)/N。S₁与S₂分别是【y_i=1对应的所有x_i的协方差矩阵】与【y_i=0对应的所有x_i的协方差矩阵】。

---

6 朴素贝叶斯分类器

数据集D={(x₁, y₁), (x₂, y₂),…,(x_N, y_N)}。有N个样本，每个样本的x_i∈R^p，每个样本的y_i∈R，且y_i∈{0,1}，i=1…N。

朴素贝叶斯法是基于贝叶斯定理与条件独立假设的分类方法。下面是朴素贝叶斯分类法的概率图（朴素贝叶斯分类法的概率图是最简单的概率图了，且是有向图，注意箭头哦）：

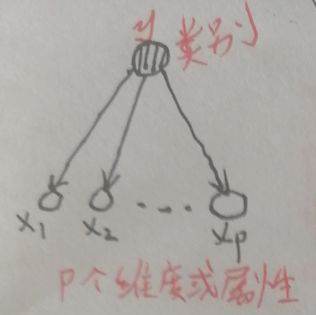
上图中，最上面为类别即输出y，且y∈{0,1}；最下面为输入x的p维特征或称为p维属性。朴素贝叶斯分类法假设在给定y的条件下有【i≠j时，x_i与x_j相互独立，即x的不同属性之间相互独立】，这就是条件独立性假设。做这种假设的动机很简单，就是为了简化计算，毕竟可能有某些特征之间有关联或关系，没有独立性假设的话计算比较复杂。对y的估计为：

有了独立性假设后，P(x|y)为：

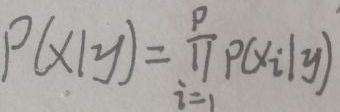
下面进行“使用范围”方面的讨论：若要解决的问题是二分类或0/1分类问题，可以假设y服从伯努利分布；若要解决的问题是多分类问题，可以假设y服从类别分布。其实二项分布就是做了n次的伯努利分布，多项分布就是做了n次的类别分布。当x是离散变量时，可以假设x的每个维度x_i服从类别分布；当x是连续变量时，可以假设x的每个维度x_i服从正态分布；

从实际来说，具体情况具体分析，up主未作讨论，我也就不展开了（写这篇文章已经花了3天时间了）。

---

END