动态规划篇
先放总结
物品是否无限
1.01背包(物品唯一):
a. 二维数组:无嵌套顺序、j遍历顺序限制;
b. 一维数组:承重j必须逆序(保证物品唯一),嵌套必须先物品i后承重j(保证dp含义);
保证物品唯一的思想:
在二维数组中,每遍历一个物品时,都是判断当前一个物品i对所有重量j的影响。后续的物品i + 1遍历时,也是使用一个物品i时的情况dp[i][j] = dp[i - 1][j - w[i]],没有发生同一个物品的dp数据被复用(dp[i][j] = dp[i][j - w[i]] + v[i])。
2.完全背包(物品数量无限):一维数组:无嵌套顺序限制,必须书包承重j正序(保证物品无限,可被重用);
保证物品数量无限制使用的思想:
使用一维数组并且j正序遍历,使得当前物品的dp数据被复用,dp[j] = dp[j - w[i]] + v[i],也就发生了同一个物品不断被使用的情况。
组合问题
1.组合:嵌套先物品i,后承重j,计算组合数;
2.排列:嵌套先承重j,后物品i,计算排序数;
递推公式
1.背包装满最大价值:
二维数组:dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); (dp[0] = 0,后续需手动初始化)
滚动数组: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); (初值为dp[0] = 0, 后续可自动初始化)
2.装满背包有几种方法:dp[j] += dp[j - nums[i]]; (初值为dp[0] = 1)。
3.装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j])
动态规划五部曲:
- dp数组以及其下标的含义;
- 递推公式
- dp数组如何初始化
- 遍历顺序
- 打印dp数组(检查)
01背包(二位数组)
有N件物品和一个最多能承重为bagSize的背包。第i件物品的重量是weight[i],得到的价值是value[i]。每件物品只能用一次,求解讲哪些物品装入背包价值总和最大。
1.dp数组以及其下标含义
我们传参int[] weight数组记录物品的重量,int[] value记录物品的价值,bagSize为背包最大承重;
这里使用的是二位dp数组,dp[i][j]这里表示的含义是:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大为多少。
2.递推公式
我们想要得到dp[i][j](从[0-i]的物品里任意取(每件物品只能用一次),放进容量为j的背包,价值总和最大是多少),有两种方向:
- 不放物品
i:当物品i的重量大于此时的承重量j时,无法将其放入。当我们不放物品i时,此时的dp[i][j]=dp[i-1][j],就是从[0-i-1]的物品里任取放进容量为j的背包最大价值和; - 放入物品
i:当物品i的重量小于等于此时的称重量j时,可以将其放入背包。此时的dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]),即为选取不放物品i时的最大价值 和 如果放入物品i时的最大价值(这里通过选取[0,i-1]物品放入承重j-weight[i]时的最大价值加上物品i的价值);
3.初始化
这里提供两种初始化的思路(更推荐第一种):
- 手动初始化:手动实现自动化初始化的第一层遍历
dp数组大小定为dp[weight.length][bagSize + 1],这里bagSize + 1是因为我们需要书包承重为0时的最大价值和,所以对于j多了一种状态;
因为dp[i][0]表示的是背包承重为0时装入的最大价值,所以设定值为0;
for (int j = 0 ; j < weight[0]; j++) {
// 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。
dp[0][j] = 0;
}
物品i此时从0开始计位,通过递归公式可以看出当前的价值是通过左上斜方获得的,所以我们需要给第一行进行初值赋值。此时的dp[0][j]表示的是选择0物品时,在承重为j的情况下最大价值和。当遍历到的承重量j大于等于物品0的重量时,它的最大价值和就是物品0的价值;

所以第一行的初始化从承重量j为物品0的重量开始遍历,直到背包最大承重量,最大价值都赋值为物品0的价值(因为此时只能装入一件物品0);承重量j小于物品0的时候都默认最大价值为0了;
for(int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
- 自动初始化,拓宽i,虚建物品0:
dp数组大小定为dp[weight.length + 1][bagSize + 1],这里行和列都多了一组数据,真正的物品下标是从1开始计位。dp[0][j]可以看成是不存入物品时背包的装入的最大价值,所以设定值为0(实际上我们是虚建了一个物品0,他的价值为0,所以即使装入背包价值总和也为0);dp[i][0]表示的是背包承重为0时装入的最大价值,所以设定值为0;

由于新建dp数组默认所有值为0,所以我们便不再需要进行其他的手动初始化;实际上这么做是简化了上一种初始化的工作,真正第一个物品这一行也就是dp[1][j]对应着上一种初始化方法的dp[0][j],而这一行的值直接由递推公式帮我们代办了;
4.遍历顺序
这道题是有两个遍历维度的:物品与背包承重量。
那么是先遍历物品还是先遍历背包承重量呢?
对于这道题是都可以的!那是因为什么呢?
理解递归的本质和递推的方向:
递归公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);可以看出dp[i][j]的得出是靠dp[i-1][j]和dp[i-1][j-wieght[i]]推导出来的,也就是左上方(包括正上方)。

如果按照先遍历背包承重量j,再遍历物品i:

如果按照先遍历物品i,再遍历背包承重量j:

两个遍历次序虽然不同,但是dp[i][j]需要的就是左上角(包括正上方)的数据,遍历顺序并不影响公式的推导!
5.打印dp数组检查检查是否符合预期
完整代码:
- 第一种手动初始化方法:
public class Solaution01bag {
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize) {
int wLen = weight.length;
//手动初始化dp数组物品i维度为真实物品数量
int[][] dp = new int[wLen][bagSize + 1];
//手动初始化
for(int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
//这两种初始化方法,i,j都是从1开始遍历(j=0已经初始化为0了,i=0手动初始化赋值了);i值的遍历范围两种方法是不同的;
for(int i = 1; i < wLen; i++) {
for (int j = 1; j < bagSize + 1; j++) {
if(weight[i] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
for(int i = 0; i < wLen; i++) {
for(int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.println('\n');
}
}
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagSize = 4;
testWeightBagProblem(weight, value, bagSize);
}
}
输出dp数组:
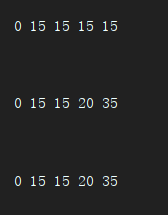
- 第二种自动初始化方法:
public class Solaution01bag {
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize) {
int wLen = weight.length;
//物品+1,虚建价值为0的物品0,默认值0免去了初始化
int[][] dp = new int[wLen + 1][bagSize + 1];
//这两种初始化方法,i,j都是从1开始遍历(j=0已经初始化为0了,i=0也初始化为0了);i值的遍历范围两种方法是不同的;
for(int i = 1; i < wLen + 1; i++) {
for (int j = 1; j < bagSize + 1; j++) {
if(weight[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
for(int i = 0; i <= wLen; i++) {
for(int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.println('\n');
}
}
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagSize = 4;
testWeightBagProblem(weight, value, bagSize);
}
}
输出dp数组:

01数组(卷动数组\一维数组)
二维动态数组的递推公式是:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
我们可以发现,新元素的诞生来自于左上方(包括正上方)的元素,也就是说我们是由压缩的空间的,就是将dp[i-1]那一层拷贝到dp[i]上,表达式就是dp[i][j] = max(dp[i][j], dp[i][j-weight[i]] +value[i])。
上述递推公式第一维度都为i,这里可以看出新元素的诞生完全可以由同一行得出,也就是一维数组就可以实现:
dp[j] = max(dp[j], dp[j-weight[i]]+value[i];
这里开始递归五部曲
1.确定dp数组的定义:
在一维数组dp中,dp[j]表示,容量为j的背包,所背的物品价值最大为dp[j](每件物品有且仅有一件)。
2.一维dp数组的递推公式
由上方的推导可知:
如果不放入物品i;
dp[j] = dp[j];
如果放入物品i:
dp[j] = max(dp[j], dp[j-weight[i]] +value[i]);
3.一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值最大为dp[j];
dp[0]表示的是容量为0的背包,所以能背负的最大物品价值为0;
那么dp数组除了下标为0的位置初始为0,其他下标该如何初始化呢?
这里和二维数组略有不同,因为一维dp数组省去了物品i这一维度,我们的无从虚建价值为0的物品0;重点是我们要从第一个物品开始遍历,也就是说我们可以自动初始化,这里看一下我们的递推公式:
dp[j] = max(dp[j], dp[j-weight[i]] +value[i]);
也就是初始化后的第一个物品遍历时当我们承重可以接纳物品时,要让原本的dp[j]被覆盖掉,所以这里我设置初始化的dp[j]为0即可(默认物品价值为正数);
所以我们的初始化值都定为0即可!
4.一维dp数组遍历顺序
这里与二维dp数组非常不同,先说结论这里的书包承载量j是逆序遍历!
原因:
先看二维dp数组的遍历:

二维dp数组在进行新元素计算dp[i][j]时,使用的是上一个物品(左上方包括正上方的元素)dp[i-1][..],左上方的元素已经定下来并不会受新元素的计算的影响;
但是当我们只有一维dp数组时,如果采用正序运算,就相当于我们我们通过上一层物品计算出新值后又覆盖到了上一层元素中,如下图所示。这样就会影响下一个新元素的计算,因为正常上一层的元素定下来后是不能被更改的;

如果我们按照这种错误的方式进行计算就相当物品不止放入了一次;
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历:
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
但是正常如果物品只能放入一次,dp[2]也应该是15,此时却放入了两次使其价值为30;
解决:
倒叙! 书包承重从大到小进行遍历,这样为什么能够避免重复放入呢?
因为我们新元素的生成都是使用左上方(包括正上方)的元素,而上一层右上方的元素是不会使用的。所以我们从后向前进行计算,新值覆盖掉了上一层的旧值并不会影响下一个新值的计算了。
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
还有一个遍历顺序的问题,这里不能够和二维dp数组一样任意选择先遍历物品还是书包承重量了。
一维dp数组一定是先遍历物品后遍历承重量!
如果颠倒了顺序,由于书包承重量是倒叙遍历,相当于在推导每一种承重时能装下一个最大价值的物品;
例:
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
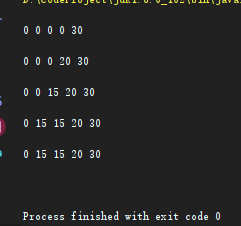
5.举例推导dp数组
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;

代码:
public class Solution01BagbyScrollArray {
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight) {
int wLen = weight.length;
//默认初始化为0
int[] dp = new int[bagWeight + 1];
for(int i = 0; i < wLen; i++) {
//这里的倒序递推包含了新元素值的判定条件,当书包承重量小于当前物品的重量时,那新值就是上一层的旧值(无需进行操作);
for(int j = bagWeight; j >= weight[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
//这里输出dp数组
for(int n = 0; n <= bagWeight; n++) {
System.out.print(dp[n] + " ");
}
System.out.print('\n');
}
}
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
testWeightBagProblem(weight, value, bagWeight);
}
}
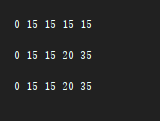
完全背包
完全背包和01背包不同之处在于,完全背包的每件物品数量无限,同一件物品可以多次放入;而01背包每件物品只有一件。
具体问题:
背包最大重量为4。
物品为:
重量 价值
物品0 1 15
物品1 3 20
物品2 4 30
每件商品有无限个,问背包能背的物品最大价值是多少?
完全背包和01背包的滚动数组非常相似!
1.我们在介绍01背包滚动数组时,在讲解遍历顺序时要求遍历j时,要求一定要逆序(从大到小)进行,这是因为递推公式:
如果放入物品i:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
如果不放入物品i:
dp[j] = dp[j];
我们在进行计算新的dp[j]值时,需要使用左侧(包括本身)的值,如果是正序遍历j,会导致物品装入多次(具体内容看上方卷动数组内容)。
完全背包计算
对于完全背包,我们正是需要物品可以装入多次,进行累计的计算dp[j]!所以完全背包承重量j的遍历是正序的!
2.01背包滚动数组的i,j两层嵌套顺序不能颠倒,不然会导致dp[j]记录的是能存下一个最大物品的价值。
完全背包是可以任意转换for中i,j两层嵌套顺序的!
因为根据递推公式,只要dp[j]左侧的元素计算出来了就好,而i,j分别都是正序遍历的,所以不受影响;
先遍历i,再遍历j:

先遍历j,再遍历i:

代码:
package com.jiayuleng.leetcode;
public class SolutionInfiniteBag {
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize) {
int[] dp = new int[bagSize + 1];
int wLen = weight.length;
for(int i = 0; i < wLen; i++) {
for(int j = weight[i]; j <= bagSize; j++) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
for(int j = 0; j <= bagSize; j++) {
System.out.print(dp[j] + " ");
}
System.out.print("\n");
}
}
public static void main(String[] args) {
int[] weight = new int[]{1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
testWeightBagProblem(weight, value, 4);
}
}
结果:
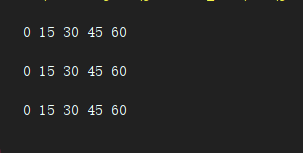
完全背包二维数组详解(了解)
我们定义:dp[i][j] 表示前 i 件物品放入一个容量为 j 的背包可以获得的最大价值(每件物品有无限个)。
每件物品可以被选择多次,因此 dp[i][j] 应为以下所有可能方案中的最大值:
- 第
i件物品选 0 个,dp[i][j] = dp[i - 1][j]; - 第
i件物品选1个,dp[i][j] = dp[i - 1][j - weight[i]] + value[i]; - 第
i件物品选2个,dp[i][j] = dp[i - 1][j - 2 * weight[i]] + 2 * value[i];
… - 第
i件物品选 k个,dp[i][j] = dp[i - 1][j - k * weight[i]] + k * value[i];
注,第 i 件物品放入 k件前提为,k * weight[i] <= j;
此时取最大值即可得递推公式为:
dp[i][j] = max{ dp[i - 1][j - k * weight[i]] + k * value[i] },0 <= k * weight[i] <= j;
进行状态空间优化
(1) dp[i][j] = max{ dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i], ... , dp[i - 1][j - k * weight[i]] + k * value[i] },0 <= k * weight[i] <= j;
(2) dp[i][j - weight[i]] = max{ dp[i - 1][j - weight[i], dp[i - 1][j - 2 * weight[i]],... ,dp[i - 1][j - k * weight[i]] + (k - 1) * value[i] },weight[i] <= k * weight[i] <= j;
观察发现,(2)式与(1)式中的后 k 项刚好相差了一个 value[i] ,将(2)式代入(1)式可得简化后的「完全背包问题」的「状态转移方程」为:
dp[i][j] = max{ dp[i - 1][j], dp[i][j - weight[i]] + value[i] };
对比:
- 0-1背包:
dp[i][j] = max{ dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i] };
滚动数组(逆序):dp[j] = max{ dp[j], dp[j - weight[i] + value[i] } - 完全背包:
dp[i][j] = max{ dp[i - 1][j], dp[i][j - weight[i] + value[i] };
滚动数组(正序):dp[j] = max{ dp[j], dp[j - weight[i] + value[i] }
目标和
力扣链接

这道题目如何和动态规划进行联系呢?
提供的数组元素分为两部分,一部分为前面为+的整数,一部分为前面为-的整数(但是元素本身都是为非负整数)。所以我们设所有元素的总和为sum,前面添加符号为+的元素之和为pos,前面添加符号为-的元素之和为neg;我们需要的目标整数位target;
包含运算关系:
pos + neg = sum => neg = sum - pos;一式
pos - neg = target将一式带入=>pos - (sum - pos) = 2 * pos - sum = target => pos = (target + sum) / 2;
我们得到的最终式子为 pos = (target + sum) / 2;
target与sum(数组元素之和)都是已给条件,所以我们可以得知要添加符号为+的元素之和pos为多少,这个pos就是01背包问题中的背包容量bagSize。 已给数组元素就是背包问题中的物品重量,
这里和01背包问题不一样的是,所要求的不是最多能装多少,而是装满有几种组合!(组合问题)
ps:大家看到(S + sum) / 2 应该担心计算的过程中向下取整有没有影响。
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
if ((target + sum) % 2 != 0) return 0; // 此时没有方案
if (Math.abs(target) > sum) return 0; // 此时没有方案
这里可以开始递归五部曲了:
1.确定dp数组以及下标含义
滚动数组(一维数组):
dp[j]表示:承载量为j(符号为+的元素之和为j)的背包,有dp[j]种组合;
二维数组:
dp[i][j]表示:使用[0, i]的物品(数组下标为[0, i]的元素),能够填满承载量为j(符号为+的元素之和为j)的背包,有d[i][j]种组合;
2.确定递推公式
dp[j]可以由前面的哪些元素构成呢?
当我们遍历到元素nums[i]时,j可以由j - nums[i] + nums[i]构成;也就是当背包承载量j可以容纳nums[i]时,dp[j - nums[i]]个组合都可以组成j;
同样如果遍历的是元素nums[i-1], j可以由j - nums[i-1] + nums[i]构成;当背包承载量j可以容纳nums[i-1]时,dp[j - nums[i-1]]个组合都可以组成j;
所以dp[j]要把遍历到的元素可以组合的方法作和:dp[j] += dp[j-nums[i]];
组合类问题公式都类似如此:
dp[j] += dp[j - nums[i]]
3.dp数组初始化
从递推公式中可以看出,dp[0]是公式中一切递推结果的起源,所以dp[0]必定不能为0,不然递推结果将都为0;dp[0]初始化为1,表示含义为当符号为+的元素之和为0时,有一种组合就是元素符号全为-(因为元素都为非负整数)
4.遍历顺序
滚动数组(一维数组):
01背包中滚动数组要求物品i的遍历在外,书包承重量j的遍历在内,且j的遍历需为倒序;
二维dp数组:
01背包中二维dp数组,i, j嵌套顺序任意,j遍历顺序无特殊要求;
5.推导dp数组验证
例:
输入:nums = [1, 1, 1, 1, 1], target = 3
pos(bagSize) = (target + sum) / 2 = (3 + 5) / 2 = 4

public class Solution494findTargetSumWays {
public static int findTargetSumWays(int[] nums, int target) {
int len = nums.length;
int sum = 0;
for(int num : nums) {
sum += num;
}
if((target + sum) % 2 != 0 && Math.abs(target) > sum) {
return;
}
//符号为正数的元素之和
int bagSize = (target + sum) / 2;
//建立一维dp数组
int[] dp = new int[bagSize + 1];
dp[0] = 1;
for(int i = 0; i < len; i++) {
for(int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
for(int j = 0; j <= bagSize; j++) {
System.out.print(dp[j] + " ");
}
System.out.println("");
}
return dp[bagSize];
}
public static void main(String[] args) {
int[] nums = {1, 1, 1, 1, 1};
findTargetSumWays(nums, 0);
}
}
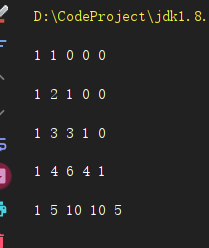
零钱兑换II(计算组合数)
力扣链接

这道我们如何转换成动态规划呢?
这道题目和上一个题目目标十分相似,但是不同的是目标和已给的元素是有限的(01背包问题),这儿道题目的元素是无限的(完全背包问题)。
动规五部曲:
1.dp数组以及下标含义
我们根据完全背包问题可以设置一维dp数组,已给的amount是背包问题里的bagSize,coins[]则对应。dp[j]表示的含义是凑成总金额j的货币组合数为dp[j]。
2.递推公式
这道题目计算的数值和上一个问题目标和一样,计算组合总和,dp[j]就是所有的dp[j-coins[i]]相加;
组合问题一般的递推公式都为:dp[j]+=dp[j-coins[i]] ;
3.dp数组如何初始化
初始化问题和目标和一样,dp[0]为1,因为dp[0]是递推公式的源头。dp[0]表达的意义为凑成总金额0的货币组合数为1;
4.确定遍历顺序
本体为完全背包问题,完全背包问题,物品i与书包承载量j的嵌套顺序是没有限制的;
但是这道题目有些许不同!首先这道题目是一个组合问题。 完全背包所求的是承载量下总价值,在计算的过程中元素顺序并不影响结果;组合问题是计算的正是元素之间的组合,和顺序是有关系的,循环的嵌套顺序影响着结果是否和顺序相关;
ps: 这里要说明一下组合问题和顺序之间的关系,这里就要先区分一下组合和排列:比如已给出两个数组[1, 5], [5, 1],对于组合问题来说这两个数组是一个组合,顺序并不影响组合;对于排列问题来说这两个数组是两个排列;
所以我们要求计算的dp[j]是不受元素顺序影响的结果。
这里我们给出一组样例数据
coins[] = [1, 5];
amount = 6;
正确的嵌套顺序应该为(组合数计算):外层for遍历物品(钱币数组coins[]),内层for遍历书包承载量(钱币总额amount);
for(int i = 0; i < coins.size(); i++) {
for(int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
遍历结果:

这里相当于第一次只计算coin[0](1)下的金额情况,第二次再计算coin[1](5)下的金额组合情况,这样只会统计一次[1,5];
排列数计算:外层为金额总数amount,内层为金币数组coins[];
for(int j = 0; j <= amount; j++) {
for(int i = 0; i < coins.length; i++) {
if(j - coins[i] >= 0) {
dp[j] += dp[j - coins[i]];
}
}
}

这样的嵌套顺序使得每一个金额数j都放入了coins[0](1)、coins[1](5)进行计算。下一个金额数在计算dp[j]时,使用之前的dp[j - coins[i]]都经过了coins[0](1)、coins[1](5)计算,所以形成了连锁累积效应,分别计算了[5,1],[1,5];
5.推导dp数组
输入:
coins = [1, 2, 5];
amount = 5;
public class Solution518change {
public static int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for(int i = 0; i < coins.length; i++) {
for(int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
for(int tmp : dp) {
System.out.print(tmp + " ");
}
System.out.println("");
}
return dp[amount];
}
public static void main(String[] args) {
int amount = 5;
int[]coins = new int[]{1, 2, 5};
change(amount, coins);
}
}
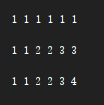
零钱兑换(凑总金额所需最小物品个数)

首先明确这道题:硬币数量无限,无限背包问题(一维dp数组,总额j需正序,无嵌套顺序限制);
递归五部曲:
1.dp[j]数组含义:
组成总额j所需最少硬币个数为dp[j];
声明:dp[amount + 1];
2.递推公式:
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
3.初始化
这里的初始化与之前的略有不同,dp[0]表示总金额为0所需钱币的个数,一定为dp[0] = 0;
因为要求的是一个最小值,再根据递推公式,我们要求其他下标非0的元素,所以下标非0元素设定成一个可以被所求最小值覆盖的数,我们设定为最大值Integer.MAX_VALUE;
4.遍历顺序
1.因为是完全背包问题:一维数组,j要求正序,嵌套顺序无限制;
2.再看题目与组合或排列无关,所以嵌套顺序无限制;
5.推导dp数组
public class Solution322coinChange {
public static int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
int max = Integer.MAX_VALUE;
for(int j = 0; j <= amount; j++) {
dp[j] = max;
}
dp[0] = 0;
for(int i = 0; i < coins.length; i++) {
for(int j = coins[i]; j <= amount; j++) {
if(dp[j - coins[i]] != max) {
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
for(int j = 0; j <= amount; j++) {
System.out.print(dp[j] + " ");
}
System.out.println("");
}
return dp[amount] == max ? -1 : dp[amount];
}
public static void main(String[] args) {
int[] coins = new int[]{1, 2, 5};
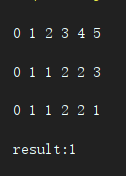
int result = coinChange(coins, 5);
System.out.println("result:" + result);
}
}
数组问题
最大子序和

1.dp数组含义
dp[i]表示以num[i]结尾的最大子数组和。
这里为什么要定义以num[i]结尾的子数组呢?
这里说一下无后效性:
为了保证计算子问题能够按照顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响,这个条件也叫做无后效性。
这里如果我们定义dp[i]为经过num[i]的最大子数组和,这里就会产生有后效性,因为我们不知道num[i]位于子数组的哪个位置。当我们定义为以num[i]为子数组的结尾时,已经求解的计算不再受后续计算的影响。
2.递推公式
递归函数,以nums[i]结尾的最大子序列和,有两种情况:
- 一种是以
nums[i-1]结尾的最大子序和加上nums[i] - 一种是以
nums[i]开头、结尾,
这里采用的方式是,选取两种情况里的最大值。
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
也可以通过判断dp[i-1]>0?进行选择,当dp[i-1]>0时,选取dp[i-1]+nums[i]不然选取num[i];
dp[i] = dp[i-1] > 0? dp[i-1] + nums[i] : nums[i];
3.dp数组初始化
初始化,dp[0]为以nums[0]开头、结尾,所以dp[0] = nums[0];
4.dp数组遍历顺序
根据dp[i]的定义,子数组是从从左向右计算的,所以递推公式中dp[i]依赖于dp[i - 1]的状态,需要从前向后遍历。
5.程序
class Solution {
//动态规划
public int maxSubArray(int[] nums) {
// dp[i]表示以nums[i]结尾的最大子序和
int[] dp = new int[nums.length];
// 初始化,dp[0]为以nums[0]开头、结尾,所以dp[0] = nums[0];
dp[0] = nums[0];
int max = dp[0];
for(int i = 1; i < nums.length; i++) {
// 递归函数,以nums[i]结尾的最大子序列和,有两种情况:
// 1.一种是以nums[i-1]结尾的最大子序和加上nums[i]
// 2.一种是以nums[i]开头、结尾,
// 这里采用的方式是,选取两种情况里的最大值。
// 也可以通过判断dp[i-1]>0?进行选择,当dp[i-1]>0时,选取dp[i-1]+nums[i];不然选取num[i];
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
// 每一次计算都要更新一次最大值,因为我们不知道要以哪个nums[i]结尾的子序和最大。
max = Math.max(dp[i], max);
}
return max;
}
}
乘积最大子数组

1.dp数组
这道题目和 最大子数组和 是同类型的题目,最大子数组和dp数组为dp[i]:以nums[i]结尾的子数组最大和。
由于乘积的性值,负数会导致最大的变最小的,最小的变最大的。因此除了维护当前最大值max,还需要维护当前最小值min。
int[] dpMax = new int[nums.length];
int[] dpMin = new int[nums.length];
这里设置最小乘积的dp数组,是因为遍历到元素为负数时,最大乘积一下就会变成最小乘积,但是后续还可能会遍历到负数使得结果再次改变,所以要记录最小乘积;
递推函数
由于乘积的性质,我们每遍历新元素num[i],要计算一下以nums[i]结尾的最大子数组乘积,与最小子数组乘积;
以nums[i]结尾的最大子数组乘积dpMax[i]有三种可能:
- 以nums[i-1]结尾的最大子数组乘上num[i],即dpMax[i] = dpMax[i-1] * nums[i];
- 以nums[i-1]结尾的最小子数组乘积乘上nums[i](满足这种情况下最大是因为dpMin[i-1]是负数,num[i]也是负数);
即dpMax[i] = dpMin[i-1] * nums[i]; - dpMax[i] = nums[i];这种情况是因为之前遍历过元素0,计算出的dpMax[i-1] = 0,dpMin[i-1]=0,此时相当于以nums[i]开头、结尾。
所以遇到元素0,就要重新开始子数组并计算乘积;
以nums[i]结尾的最小子数组dpMin[i]同理,也是三种情况。
dpMax[i] = Math.max(dpMax[i - 1] * nums[i], Math.max(dpMin[i - 1] * nums[i], nums[i]));
dpMin[i] = Math.min(dpMax[i - 1] * nums[i], Math.min(dpMin[i - 1] * nums[i], nums[i]));
3.dp数组初始化
以nums[0]结尾的最大、最小子数组都是nums[0]。
dpMax[0] = nums[0];
dpMin[0] = nums[0];
4.遍历顺序
由递推公式知,从左向右遍历数组。
5.程序
class Solution {
// 动态规划
// 这道题目和 最大子数组和 是同类型的题目,最大子数组和dp数组为dp[i]:以nums[i]结尾的子数组最大和。
// 由于乘积的性值,负数会导致最大的变最小的,最小的变最大的。因此除了维护当前最大值max,还需要维护当前最小值min。
public int maxProduct(int[] nums) {
// dp数组含义
// dpMax[i]:以nums[i]为结尾的子数组最大乘积为dpMax[i];
// dpMin[i]: 以nums[i]为结尾的子数组最小乘积为dpMin[i];
// 这里设置最小乘积的dp数组,是因为遍历到元素为负数时,最大乘积一下就会变成最小乘积,但是后续还可能会遍历到负数使得结果再次改变,所以要记录最小乘积;
int[] dpMax = new int[nums.length];
int[] dpMin = new int[nums.length];
dpMax[0] = nums[0];
dpMin[0] = nums[0];
int max = dpMax[0];
for(int i = 1; i < nums.length; i++) {
// 递推函数
// 由于乘积的性质,我们每遍历新元素num[i],要计算一下以nums[i]结尾的最大子数组乘积,与最小子数组乘积;
// 以nums[i]结尾的最大子数组乘积dpMax[i]有三种可能:
// 1.以nums[i-1]结尾的最大子数组乘上num[i],即dpMax[i] = dpMax[i-1] * nums[i];
// 2.以nums[i-1]结尾的最小子数组乘积乘上nums[i](满足这种情况下最大是因为dpMin[i-1]是负数,num[i]也是负数);
// 即dpMax[i] = dpMin[i-1] * nums[i];
// 3.dpMax[i] = nums[i];这种情况是因为之前遍历过元素0,计算出的dpMax[i-1] = 0,dpMin[i-1]=0,此时相当于以nums[i]开头、结尾。
// 所以遇到元素0,就要重新开始子数组并计算乘积;
// 以nums[i]结尾的最小子数组dpMin[i]同理,也是三种情况。
dpMax[i] = Math.max(dpMax[i - 1] * nums[i], Math.max(dpMin[i - 1] * nums[i], nums[i]));
dpMin[i] = Math.min(dpMax[i - 1] * nums[i], Math.min(dpMin[i - 1] * nums[i], nums[i]));
max = Math.max(dpMax[i], max);
}
return max;
}
}
最长重复子数组

1.dp数组
dp[i][j]含义:以nums1[i]结尾的数组与以nums2[j]结尾的数组的最长重复子数组;
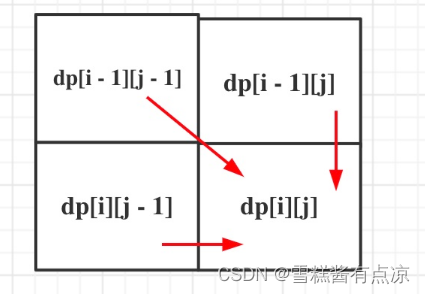
这里要注意,以nums1[i]结尾与以nums2[j]结尾的数组,在比对时是nums1[i]与nums2[j]对齐进行比较,也就是尾对齐后比较重复子数组的。
这里采用尾对齐的比较方式是因为,我们在计算dp[i][j]即遍历新元素nums1[i]与nums2[j]时,进行的判断为nums1[i]==nums2[j]?即尾对齐的比较,所以我们要求上一次遍历的dp[i-1][j-1]也是尾对齐的才可。
2.递推公式
因为是尾对齐的比较,当前遍历元素nums1[i]==nums2[j]时,即新增公共尾节点,取以nums1[i-1]与nums2[j-1]为为节点并尾对齐比较的最大重复长度 + 1;
若nums1[i]!=nums2[j],则nums1[i]与nums2[j]不能当作尾节点进行尾对齐比较,所以dp[i][j]=0。
dp[i][0] = nums1[i] == nums2[0]? dp[i - 1][j - 1] + 1 : 0;
这里也是这道题比较难想的地方,因为我们没有采用任意对齐比较的方式(记录子数组所有重复长度的可能),所以我们并不是在dp数组最后就能得到最大重复长度,而是要每一次计算dp[i][j]都进行一次最大值的比较。
注:如果采用任意对齐比较的方式,我们的判断条件nums1[i]==nums2[j]?无法保证nums[i-1]与nums[j-1]的是否相等。任意对齐留下的状态可能是很早之前对齐比较相等的,很难统计。
3.初始化
初始化,同样是尾对齐比较,dp数组第一列元素dp[i][0]与第一行元素dp[0][j],因为都是一个元素与一个数组尾对齐比较,只有两种情况1个最大重复,或者0;
4.遍历顺序
无影响
5.程序
class Solution {
// 动态规划
public int findLength(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
// dp[i][j]含义:以nums1[i]结尾的数组与以nums2[j]结尾的数组的最长重复子数组;
// 这里要注意,以nums1[i]结尾与以nums2[j]结尾的数组,在比对时是nums1[i]与nums2[j]对齐进行比较,也就是尾对齐后比较重复子数组的。
// 这里采用尾对齐的比较方式是因为,我们在计算dp[i][j]即遍历新元素nums1[i]与nums2[j]时,
// 进行的判断为nums1[i]==nums2[j]?即尾对齐的比较,所以我们要求上一次遍历的dp[i-1][j-1]也是尾对齐的才可。
int[][] dp = new int[len1][len2];
int res = 0;
// 初始化,同样是尾对齐比较,dp数组第一列元素dp[i][0]与第一行元素dp[0][j],因为都是一个元素与一个数组尾对齐比较,只有两种情况1个最大重复,或者0;
dp[0][0] = nums1[0] == nums2[0]? 1 : 0;
for(int i = 1; i < len1; i++) {
dp[i][0] = nums1[i] == nums2[0]? 1 : 0;
res = Math.max(dp[i][0], res);
}
for(int j = 1; j < len2; j++) {
dp[0][j] = nums1[0] == nums2[j]? 1 : 0;
res = Math.max(dp[0][j], res);
}
// 递推公式
// 因为是尾对齐的比较,当前遍历元素nums1[i]==nums2[j]时,即新增公共尾节点,取以nums1[i-1]与nums2[j-1]为为节点并尾对齐比较的最大重复长度 + 1;
// 若nums1[i]!=nums2[j],则nums1[i]与nums2[j]不能当作尾节点进行尾对齐比较,所以dp[i][j]=0。
// 这里也是这道题比较难想的地方,因为我们没有采用任意对齐比较的方式(记录子数组所有重复长度的可能),所以我们并不是在dp数组最后就能得到最大重复长度,而是要每一次计算dp[i][j]都进行一次最大值的比较。
// 注:如果采用任意对齐比较的方式,我们的判断条件nums1[i]==nums2[j]?无法保证nums[i-1]与nums[j-1]的是否相等。任意对齐留下的状态可能是很早之前对齐比较相等的,很难统计。
for(int i = 1; i < len1; i++) {
for(int j = 1; j < len2; j++) {
dp[i][j] = nums1[i] == nums2[j]? dp[i - 1][j - 1] + 1 : 0;
res = Math.max(dp[i][j], res);
}
}
return res;
}
}
最长公共子序列

这道题目与上一道最长重复子数组的区别是,这里计算公共的部分可以是不连续的。
1.dp[i][j]含义:
这里也是尾对齐比较,dp[i][j]表示数组1在[0, i - 1]范围与数组2在[0, j - 1]范围的最长公共子序列长度。建立dp数组长度为,int[len1 + 1][len2 + 1],这里两个数组的长度各扩展了一位,用于表示当数组范围为[0, 0]也就是无元素的情况,可以简化初始化。
2.递推公式
与上一题不同,最长公共子序列不要求公共元素是连续的。
当尾对齐比较元素相同时nums1[i - 1] == nums2[j - 1],与上一题情况相同,新增一位公共元素,此元素为新的公共子序列的尾元素,dp[i][j] = dp[i - 1][j - 1] + 1。
当尾对齐比较元素不相同时nums1[i - 1] != nums2[j - 1],我们可以继承此前的已计算好的状态,有两种可选继承的状态,分别是dp[i - 1][j], dp[i][j - 1],dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])。这里为什么不考虑dp[i - 1][j - 1]呢,是因为根据dp的定义,dp[i - 1][j - 1] 一定是<= dp[j - 1][i] 或者 dp[i][j - 1]的,所以省略掉了。
3.初始化
dp[0][i]表示数组1无元素,dp[i][0]表示数组2无元素,此两种情况都没有公共子序列所以都为0。
4.遍历顺序
根据递推公式,只要 i, j 都是正序遍历即可,嵌套顺序无影响。
5.程序
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int len1 = text1.length(), len2 = text2.length();
// 1.这里也是尾对齐比较,dp[i][j]表示数组1在[0, i - 1]范围与数组2在[0, j - 1]范围的最长公共子序列长度。
// 两个数组的长度各扩展了一位,用于表示当数组范围为[0, 0]也就是无元素的情况,可以简化初始化。
int[][] dp = new int[len1 + 1][len2 + 1];
// 3.dp[0][i]表示数组1无元素,dp[i][0]表示数组2无元素,此两种情况都没有公共子序列所以都为0。
// 4.根据递推公式,只要 i, j 都是正序遍历即可,嵌套顺序无影响。
for(int i = 1; i <= len1; i++) {
for(int j = 1; j <= len2; j++) {
// 2.当尾对齐比较元素相同时nums1[i - 1] == nums2[j - 1]
// 此元素为新的公共子序列的尾元素
if(text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
// 当尾对齐比较元素不相同时`nums1[i - 1] != nums2[j - 1]`,我们可以继承此前的已计算好的状态
// 有两种可选继承的状态,分别是dp[i - 1][j], dp[i][j - 1]
// 这里为什么不考虑dp[i - 1][j - 1]呢,是因为根据dp的定义,dp[i - 1][j - 1] 一定是<= dp[j - 1][i] 或者 dp[i][j - 1]的
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 5.dp状态一直留到了最后一位元素,直接返回即可。
return dp[len1][len2];
}
}
股票问题
买卖股票的最佳时机

1.dp数组
设dp数组dp[n][2],dp[i][0]:表示手上没有股票时最大现金额,dp[i][1]表示手上有一支股票时最大现金额。
2.递推公式
第 i 天手上没有股票时,即dp[i][0],可能有两种情况:
1.一种是上一天手上就没有股票;
2.一种是上一天买入了股票,第 i 天给卖了;
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
第 i 天手上有股票时,即dp[i][1],可能有两种情况:
1.第 i - 1 天手上就有股票了;
2.第 i - 1 天手上没有股票,第 i 天买入;
dp[i][1] = Math,max(dp[i-1][1], -prices[i])
(这里的含义,我是昨天就持有股票划算,还是今天才买入划算,这里比较的是-prices[i], -prices[i-1](i-1天买入)或-prices[i-m]的大小,所以限定了只能买入一次)
注:题目要求股票只能买卖一次,这里我们限制了买入操作。第 i 天手上持有一支股票时,即dp[i][1],其中一种情况,在第 i - 1 天手上没有股票时我们买入第 i 天的股票,dp[i][1] = -prices[i],这样使得我们每次买入都是第一次买入操作,没有使用已经计算好的第 i - 1 天手上没有股票的值dp[i][0],如果dp[i][1] = dp[i-1][0] - prices[i],则表示可以进行多次股票交易,因为第 i - 1 天手上没有股票有可能是i - 1天及之前卖掉的股票。
3.初始化
dp[0][0] = 0:第0天没买时手上现金为0;
dp[0][1] = -prices[0]:第0天买入股票手上现金为-prices[0];
4.遍历及嵌套顺序
dp[i]来自于dp[i-1],所以正序遍历即可。
5.结尾及代码
我们返回dp[n-1][0],表示的是最后一天不持有股票的最大现金额;
public int maxProfit(int[] prices) {
int days = prices.length;
int[][] dp = new int[days][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1; i < days; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
}
return dp[days - 1][0];
}
简化滚动数组:
public int maxProfit(int[] prices) {
int days = prices.length;
int[] dp = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
for(int i = 1; i < days; i++) {
dp[0] = Math.max(dp[0], dp[1] + prices[i]);
dp[1] = Math.max(dp[1], -prices[i]);
}
return dp[0];
}
买卖股票的最佳时机II

这道题目与上一道题目内容基本是一样的,不同的是这道题目说了可以多次进行交易,也就是买卖一次股票后可以继续买卖股票,求获得的最大利润。
根据上一题的分析,我们得知限制股票是否能多次进行买卖的条件是:
注:题目要求股票只能买卖一次,这里我们限制了买入操作。第 i 天手上持有一支股票时,即
dp[i][1],其中一种情况,在第 i - 1 天手上没有股票时我们买入第 i 天的股票,dp[i][1] = -prices[i],这样使得我们每次买入都是第一次买入操作,没有使用已经计算好的第 i - 1 天手上没有股票的值dp[i][0],如果dp[i][1] = dp[i-1][0] - prices[i],则表示可以进行多次股票交易,因为第 i - 1 天手上没有股票有可能是i - 1天及之前卖掉的股票。
所以直接给出程序:
public int maxProfit(int[] prices) {
int days = prices.length;
int[][] dp = new int[days][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1; i < days; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
// 这里不同
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[days - 1][0];
}
腾讯22.4.26笔试题,股票买卖(集大成者)
题目描述
现有一长度为n的数组a,表示某支股票每天的价格,每天最多买入或卖出该支股票的1手股票,买入或卖出没有手续费,且卖出股票前必须手里已经有股票才能卖出,但是持有的股票数目不受限制,并且初始资金为m元,在任意时刻不能进行透支,所以资金必须始终大于等于0,请问在n天结束后,拥有最大总资产是多少?(最大总资产为持有现金+持有的股票价格)
输入描述
第一行两个整数,n,m
第二行n个整数{ai},其中ai表示股票在第i天的售价
输出描述
输出n天结束后,拥有最大总资产
示例
输入
6 2
2 3 1 1 1 2
输出
6
说明
第1天买入1手,第2天卖出1手,第3,4,5天都买入1手,最后总持有3手股票,股票价格为2,总资产为6。
输入
3 2
1 1 4
输出
8
说明
第一天买入,第二天买入,第三天继续持有,总共持有两手股票,股票价格为4,总资产为8。
输入
3 100
10 9 8
输出
100
说明
股票一直在下跌,都不买入,现金为100,股票为0,总资产为0。
题目分析:
这道股票题目要求的依然是一支股票,给出n天的股票价格。不同的是进行一次股票买卖期间,是可以继续进行股票买卖的,即每天都可以进行一次操作:买入或卖出一手(份)股票。而且这里给出了初始现金,现金数足够才可以按价格买入股票,不可以透支。
1.dp数组
我们建立dp数组dp[n][n],dp[i][j]表示第 i 天,手上持有 j 手(份)股票的最大现金额。
2.递推公式
dp[i][j]第 i 天,持有 j 支股票,有三种可能:
1.dp[i][j] = dp[i-1][j]: 第 i-1 天就已经持有了 j 支股票;
2.dp[i][j] = dp[i-1][j-1] - price[i]: 第 i-1 天持有 j-1 支股票,买入第 i 天的股票,现金数要减去第 i 天的股票;
3.dp[i][j] = dp[i-1][j+1] + price[j]: 第 i-1 天持有 j+1 支股票,卖掉第 i 天的股票,现金数加上第 i 天的股票;
注: 2,3有一个前提,就是2要求dp[i-1][j-1]不为-1,就是前一天手上是有 j-1 支股票的;3要求dp[i-1][j+1]不为 -1,就是前一天手上是有 j+1 支股票的;若2,3的前提条件不能满足的话,则说明只能是dp[i-1][j]。
//先将默认情况赋值,之后再进行判断是否能够比较,再进行比较
dp[i][j] = dp[i - 1][j];
// j表示手上有几只股票,dp[i-1][j+1]=-1时,表示没有j+1支股票
if(j > 0 && dp[i-1][j-1] != -1 && dp[i - 1][j - 1] >= price[i]) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] - price[i]);
}
// j表示手上有几只股票,dp[i-1][j+1]=-1时,表示没有j+1支股票
if(j < n-1 && dp[i - 1][j + 1] != -1) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j + 1] + price[i]);
}
3.初值
dp[0][0] = m,第0天不持有股票时,即为初始现金额。
初始现金若可以买入第0天的股票时,买入一手:当m >= price[0], dp[0][1] = m - price[0]。
dp[0]其余值均赋值-1,这是因为初始即第0天除了这两种情况,其他情况都是不可能发生的。我们使用-1表示不可能发生,防止后续的dp数组判断将不可能发生的情况进行了递推。
4.初值
根据递推公式正序就可
5.结尾及程序
这里我们要提下结尾,我们最后得到的dp[n-1][j],表示的是最后一天持有 j 手股票时手上的最大现金额。所以我们需要根据(最大总资产为持有现金 + 持有 j 手股票 * 第n-1天股票价格)遍历计算比较出最大资产值。
注:这里与之前的股票问题返回值不同是因为,之前的股票最大只能持有1手,所以最后一天不持有股票的最大现金值即dp[n-1][0]就是所求值。实际上是这道题目返回值的简化,也可以进行遍历计算比较最大值,但是只能持有一份的股票并且每日可以进行一份股票的交易的时候,是不会有股票堆积在手中卖不完的情况,所以遍历计算出的最大值一定是dp[n-1][0](特殊情况下dp[n-1][1] + 1 * price[n-1] = dp[n-1][0])。
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[] price = new int[n];
for(int i = 0; i < n; i++) {
price[i] = scan.nextInt();
}
dynamic(price, n, m);
}
public static void dynamic(int[] price, int n, int m) {
// 股票市场一共n天(0-n-1天)
// dp[i][j]表示第i天,持有j个股票的最大现金额度
long[][] dp = new long[n][n];
Arrays.fill(dp[0], -1);
// 第0天持有m金额
dp[0][0] = m;
if(m >= price[0]) {
dp[0][1] = m - price[0];
}
for(int i = 1; i < n; i++) {
for(int j = 0; j < n; j++) {
// 递推公式,dp[i][j]第i天,持有j支股票,有三种可能:
// 1.dp[i][j] = dp[i-1][j]: 第i-1天就已经持有了j支股票;
// 2.dp[i][j] = dp[i-1][j-1] - price[i]: 第i-1天持有j-1支股票,买入第i天的股票,现金数要减去第i天的股票;
// 3.dp[i][j] = dp[i-1][j+1] + price[j]: 第i-1天持有j+1支股票,卖掉第i天的股票,现金数加上第i天的股票;
// 2,3有一个前提,就是2要求dp[i-1][j-1]不为-1,就是前一天手上是有j-1支股票的;3要求dp[i-1][j+1]不为-1,就是前一天手上是有j+1支股票的;
// dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] - price[i], dp[i - 1][j + 1] + price[i]);
dp[i][j] = dp[i - 1][j];
// j表示手上有几只股票,dp[i-1][j+1]=-1时,表示没有j+1支股票
if(j > 0 && dp[i-1][j-1] != -1 && dp[i - 1][j - 1] >= price[i]) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] - price[i]);
}
// j表示手上有几只股票,dp[i-1][j+1]=-1时,表示没有j+1支股票
if(j < n-1 && dp[i - 1][j + 1] != -1) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j + 1] + price[i]);
}
}
}
for(int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.println();
}
long res = 0;
for(int j = 0; j < n; j++) {
if(dp[n - 1][j] == -1) {
continue;
}
res = Math.max(res, dp[n - 1][j] + j * price[n - 1]);
}
System.out.println("max:" + res);
}
解法2 回溯法
回溯配合递归
static int max = 0;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[] price = new int[n];
for(int i = 0; i < n; i++) {
price[i] = scan.nextInt();
}
// List<Integer> result = new ArrayList<>();
dfs(price, n , 0, m, 0);
// System.out.println(Collections.max(result));
System.out.println(max);
}
/**
* 回溯法,每一天都有三种情况,持有、买入一份(满足条件)、卖出一份(满足条件)
* @param price:股票价格
* @param len:天数
* @param depth:当前天数
* @param out:当前现金数
* @param num:当前持有股票数
*/
public static void dfs(int[] price, int len, int depth, int money, int num ) {
// 终止条件,当前天数到达最后一天
if(depth == len - 1) {
// 计算当前情况的总资产,并和最大值比较;
max = Math.max(max, money+ num * price[depth]);
return;
}
// 当天持有股票,不操作
dfs(price, len, depth + 1, money, num);
// 当持有股票数>0时, 可以卖出股票
if(num > 0) {
dfs(price, len, depth + 1, money + price[depth], num - 1);
}
// 当前的现金数不低于当天的股票价格,可以买入一份股票
if(money >= price[depth]) {
dfs(price, len, depth + 1, money - price[depth], num + 1);
}
}
最佳买卖股票时机含冷冻期

这道题目持有股票数量最大为1,可以进行多次股票交易,特殊的地方在于持有股票卖出后,后一天进入冷冻期,无法进行交易。
这里我们要通过dp数组单独罗列几种情况,我们专注股票卖出情况是否是当天卖出,因为当天是否卖出决定着后一天是否进入冷静期。
1.dp[i][j]含义
int[][] dp = new int[days][3];
a.dp[i][0]: 第i天不持有股票,且为第i天卖出的;
b.dp[i][1]: 第i天不持有股票,不是第i天卖出的(更之前卖出的);
c.dp[i][2]: 第i天持有股票(暂不区分是否当天买入,因为持有股票并不影响冷静期);
2.递推公式:
三种情况需要分别进行递推。
a.dp[i][0]可能由前一天持有股票得到。
dp[i][0] = dp[i - 1][2] + prices[i];
b.dp[i][1]可能由昨天dp[i - 1][1]得到;也可能是昨天卖的dp[i - 1][0],今天是冷静期;
dp[i][1] = Math.max(dp[i - 1][1], dp[i-1][0]);
c.dp[i][2]可能由昨天之前卖出(今天不是冷冻期),今天买入dp[i - 1][1] - prices[i];
也可能昨天就持有了股票dp[i - 1][2];
dp[i][1] = Math.max(dp[i - 1][2], dp[i-1][1] - prices[i]);
3.初始化
dp[0][0]表示第0天,卖出股票,相当于当天买入卖出没有盈利,dp[0][0] = 0;
dp[0][1]表示第0天之前卖出股票,因为之前不能卖出所以手里的现金还是0 = dp[0][1];
dp[0][2]表示第0天持有股票手上现金数,就是第0天买入股票:dp[0][2] = -prices[0];
4.顺序
通过递推公式,虽然是二维数组,但是只需要一层循环,因为第二维数组的三种情况已经罗列出来了,外层数组需要正序进行;
5.程序
class Solution {
public int maxProfit(int[] prices) {
int days = prices.length;
// 卖出后会有一天冷冻期,我们设三种状态,不去关注冷冻期,多设一种状态关注是否是当天卖出股票
// 1.dp[i][0]:第i天不持有股票,是第i天卖出;
// 2.dp[i][1]:第i天不持有股票,不是第i天卖出,是更之前已经卖出;
// 3.dp[i][2]:第i天持有股票(可能是第i天买入,也可能是之前买入);
int[][] dp = new int[days][3];
// 初始化
// dp[0][0]相当于第0天买入又卖出,没挣到钱;
dp[0][0] = 0;
dp[0][1] = 0;
dp[0][2] = -prices[0];
for(int i = 1; i < days; i++) {
dp[i][0] = dp[i - 1][2] + prices[i];
dp[i][1] = Math.max(dp[i - 1][0], dp[i - 1][1]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] - prices[i]);
}
for(int i = 0; i < days; i++) {
for(int j = 0; j < 3; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.println();
}
return Math.max(dp[days - 1][0], dp[days - 1][1]);
}
}
因为手里不持有股票有两种情况,返回时返回这两种情况的最大值!
正则表达式匹配

1. dp数组含义确定
dp[i][j]含义为,s中范围前 i个字符是否匹配 p中前 j个模式。
这里声明的范围为boolean dp[s.length() + 1][p.length() + 1],因为dp[0][0]表示 s为空字符,p为空模式时的情况。
2. 递推公式
注:dp数组定义时,多设了一个空情况,所以s,p中第 i,j位与dp中第i, j差了一位。
1)p[j - 1]为字母字符时,s[i - 1]必须为同样的字母字符,dp[i][j] = true。
p[j - 1] = '.'时,则p[j]一定可以匹配s[i],dp[i][j] = true。
否则为 false。
2)p[j - 1]为'*'时,则可以对前一个匹配符p[j - 1]进行任意次(包括0次)匹配。
a. 当s[i - 1] = p[j - 2]时,此时*前一位匹配符与 s第 i位匹配:
这里分为两种情况,匹配 0次和匹配多次(>0)。
- 匹配 0次:此时
p[j-2], p[j - 1]不起作用,相当于删去p[j - 2]和p[j - 1],此时dp[i][j] = dp[i][j - 2]; - 匹配多次:此时相当于除去
s[i - 1],还可继续进行匹配(包括匹配0次或匹配多次,类似递归),此时dp[i][j] = dp[i - 1][j];
参考:匹配多次公式推导
b. 当s[i - 1] != p[j - 2]时,此时*前一位匹配符不与s中第 i位匹配,*与前一位匹配符只能进行匹配 0次,即丢弃p[j - 2], p[j - 1]。
此时dp[i][j] = dp[i][j - 2]。
3. 初始化
dp[0][0] = true: 表示 s为空字符,p为空模式时的情况,此时为匹配成功 true;
dp[0][j],j从 1开始,检测 *进行 0次匹配的情况:
当dp[0][j] == '*'时,dp[0][j] = dp[0][j - 2]。
dp[i][0] = false,i从 1开始,匹配符为 0个时,无法匹配;
4. 嵌套顺序
i,j嵌套顺序无影响,根据递推公式,dp[i][j]的值来自于左上方。
5. 程序
class Solution {
public boolean isMatch(String s, String p) {
// dp[i][j]含义为,s中范围前 i个字符是否匹配 p中前 j个模式;
// 这里声明的范围为s.length() + 1,p.length() + 1,因为dp[0][0]表示 s为空字符,p为空模式时的情况;
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
// dp[0][0]表示 s为空字符,p为空模式时的情况,此时为匹配成功 true;
dp[0][0] = true;
// dp[0][j],j从 1开始,检测 *进行 0次匹配的情况;
for(int j = 1; j <= p.length(); j++) {
if(p.charAt(j - 1) == '*') {
dp[0][j] = dp[0][j - 2];
}
}
// dp[i][0]为false,匹配符为 0个时,无法匹配;
for(int j = 1; j <= p.length(); j++) {
// 匹配从 1开始,dp[i][0]为false,因为匹配模式为空,无法匹配成功。
for(int i = 1; i <= s.length(); i++) {
if(s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
} else if(p.charAt(j - 1) == '*') {
// 当 s中第 i个元素(从 1起记)与 p中第 j - 1个元素不相同时,且 p中第 j - 1个元素不为'.'时,*与前一个匹配元素(j - 1)匹配 0次,不计入匹配
if(s.charAt(i - 1) != p.charAt(j - 2) && p.charAt(j - 2) != '.') {
// 当 s[i - 1] != p[i - 2] && p[i - 2] != '.'时,只能让 *匹配 0次
// *匹配 0次时,对前 i个字符串进行匹配[j - 2]。(j为 *,j-1为 *前元素)
dp[i][j] = dp[i][j - 2];
} else {
// 当 s[i - 1] == p[i - 2] || p[i - 2] != '.'时,
// *可以匹配 0次,也可以匹配多次
// 匹配多次情况为 s除去第 i个元素,[0, j]匹配模式也可以继续正常匹配。
dp[i][j] = dp[i - 1][j] || dp[i][j - 2];
}
}
}
}
return dp[s.length()][p.length()];
}
}
完全平方数
这道题目希望寻找数值由平方数组成的最小数量。可以看做成一道完全背包问题,背包中存放的是{11, 22, 33, … , nn},物品可以无限次使用,装满大小为n的背包,求最小装满数量。
完全背包问题可以通过滚动数组+正序遍历实现。
1.dp含义
dp[j]表示 j可以由完全平方数组成的最小数量为dp[j]。
int[] dp = new int[n + 1];
2.递推公式
a.当j >= i * i时,书包容量j能容下物品重量 i*i。
dp[j] = dp[j - i * i] + 1;
b.当j < i * i时,书包无法装下物品:
dp[j] = dp[j];
取两种情况下的最小值
dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
3.初始化
dp[0] = 0; 表示和为0时,由平方数组成的最小数量0。这里的0可能感觉不是很明确,可以通过dp[1]来确定,1由平方数组成的最小数量为1,而设dp[0] = 0可以推出dp[1] = 1;
因为求的是最小值,所以我们要对数组其他元素初始化设定为Integer.MAX_VALUE,使得遇到小值可以直接获取到。
4.顺序
无限背包,要求容量j遍历正序。
5.程序
class Solution {
/**
* 动态规划
* 完全背包问题,相当于物品有{1 * 1, 2 * 2 ... n * n},放入大小为 n的背包,最少放入几件物品填满;
* @param n
* @return
*/
public int numSquares(int n) {
// 1.dp[j]:和为j的完全平方数的最少数量为dp[j];
int[] dp = new int[n + 1];
// 3.初始化,因为求最小装填数,初始将元素值置为最大;
for(int j = 0; j <= n; j++) {
dp[j] = Integer.MAX_VALUE;
}
// 背包容量为 0时,装填数设为 0。这里设为0,背包容量为 1时,会根据递推公式自动设定dp[1] = 1;
dp[0] = 0;
// 4.遍历顺序,因为是完全背包问题,嵌套顺序无要求,背包容量要求正序遍历;
// 遍历物品 weight[i],物品不用所有都遍历到,当 i * i > n时,就不用了;
for(int i = 1; i * i <= n; i++) {
// 遍历背包容量,容量起点从 weight[i] = i * i开始遍历,可以省去容量j < weight[i]时的判断;
for(int j = i * i; j <= n; j++) {
// 避免Integer.MAX_VALUE + 1溢出,由于滚动数组本身dp[j] = dp[j]
if(dp[j - i * i] != Integer.MAX_VALUE) {
if(dp[j - i * i] != Integer.MAX_VALUE) {
// 2.递推数组为dp[j] = Math.min(dp[j - i * i] + 1, dp[j]);
dp[j] = Math.min(dp[j - i * i] + 1, dp[j]);
}
}
}
return dp[n];
}
}
72.编辑距离(困难)

这道题目看着很难,但是实际的程序很简单。但是要我直接想出来递推公式又很难- -
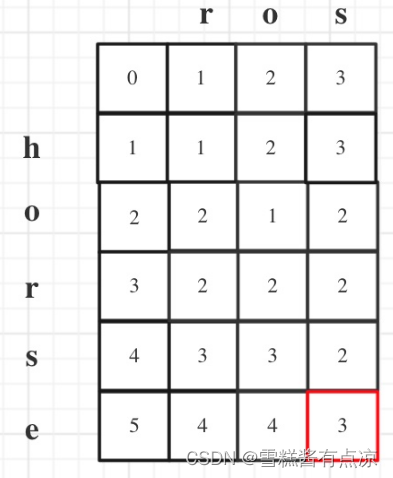
1.dp数组
设dp数组为new int[word1.length() + 1][word2.length() + 2],dp[i][j]含义为word1以i 结尾转换为word2以j 结尾的字符串最少的操作数。这里是尾对齐比较法,且word1与word2各扩充一位分别表示word1
2.递推公式
1.当word1.charAt(i) == word.charAt(j)时,尾对齐元素相同。
dp[i][j] = dp[i - 1][j - 1]
2.当word1.charAt(i) != word.charAt(j)时,尾元素不相同。此时有三种方式进行操作。
a.dp[i][j] = dp[i - 1][j] + 1,word1 [0, i - 2]已经转变为word2 [0, j - 1]了。word1增加了一位[i - 1],此时将word1[i - 1]删除掉即可。
b.dp[i][j] = dp[i][j - 1] + 1,word1 [0, i - 1]已经转变为word2 [0, j - 2]。此时word2增加了一位[j - 1],对word1进行一次增添操作即可。
c.dp[i][j] = dp[i - 1][j - 1] + 1,word1 [0, i - 2]已经转变为了word2 [0, j - 2],此时将word1新增了一位[i - 1],word2新增了一位[j - 1],但是不相等。所以执行一次替换操作将word1[i - 1]替换为word2[j - 1]即可。
取三种方式的最小值即为dp[i][j]。
dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
3.初始化
这里dp[0][0]即为word1与word2都为空时,无需进行任何操作,dp[0][0] = 1。
i > 0时,dp[i][0] = dp[i - 1][0] + 1,word2为空,word1每多框选一个元素,就需要执行一次删除操作。
j > 0时,dp[0][j] = dp[0][j - 1] + 1, word1为空,word2每多框选一个元素,就需要执行一次新增操作。
4.遍历顺序
由递推公式看出dp[i][j]由左、上、左上方得来,所以i, j均正序遍历即可,无嵌套顺序要求。
5.程序
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length(), len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for(int i = 1; i <= len1; i++) {
dp[i][0] = dp[i - 1][0] + 1;
}
for(int j = 1; j <= len2; j++) {
dp[0][j] = dp[0][j - 1] + 1;
}
for(int i = 1; i <= len1; i++) {
for(int j = 1; j <= len2 ; j++) {
if(word1.charAt(i - 1) != word2.charAt(j - 1)) {
dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
} else {
dp[i][j] = dp[i - 1][j - 1];
}
}
}
return dp[len1][len2];
}
}
小红书:最佳传送方案
当前有n座山(1-n),当前在1号山峰。每一次移动可以移动到后续距离不超过k的山峰,例k=2,在山峰1,则可以移动到山峰2或山峰3。在山峰间移动需要付出金币,若从高向低移动则不用付出金币。否则,当从低向高移动则需要付出山峰高度差的金币。
问从山峰1移动至山峰n最少需要多少金币。
1.dp定义
dp[i]为到达第i座山峰所需最少的金币。
2.递推公式
当前在第i座山峰,可能由第i - j座山峰来到(要求i - j >= 1, 0<= j <= k)。
for(int j = 0; j <= k; j++) {
dp[i] = Math.min(dp[i - j] + Math.max(h[i] - h[i - j], 0), dp[i - j]);
}
3.如何初始化
dp[0] = 0,初始在第一座山峰时,是不需要花钱的。但是剩余的山峰赋予一个极大值,方便递推公式中的比对赋值。
4.递推顺序
i要求正序遍历。
5.程序
void dynamic(int[] h, int k) {
//dp[i]为在第i山最小花钱数
int len = h.length;
int[] dp = new int[len];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for(int i = 0; i < len; i++) {
// dp[i]可能由dp[i - j]到达
for(int j = 0; j <= k && i - j >= 0; j++) {
dp[i] = Math.min(dp[i - j] + Math.max(0, h[i] - h[i - j]), dp[i]);
}
for(int num : dp) {
System.out.print(num + " ");
}
System.out.println();
}
System.out.println(dp[len - 1]);
}
139.中国人寿:单词拆分
准备一组单词卡,每张卡上有一个单词。给出一个字符串,如‘catcatdogdog’, 小明根据这个字符串,判断是否可以从手上的单词卡片组中选出单词来拼接成这个字符串,如果可以,回答true,否则回答false。
单词卡片允许重复使用,且不要求必须全部使用。
动态规划
1.dp数组定义
设dp[i]表示以s.charAt(i - 1)结尾的元素是否可以由单词拼接。dp数组多设置一位dp[0]表示字符串为空时的情况。
boolean[] dp = new boolean[s.length + 1];
2.递推公式
dp[i]可以有由dp[j], 0<= j < i 推出。如何推出呢?
当dp[j] == true且s.substring(j, i)有此单词卡,则dp[i] = true。
// 0 <= j < i;
dp[i] = dp[j] && set.contains(s.substring(j, i));
3.初始化
dp[0] = true,对字符串为空时进行赋值true。
计算dp[1]时,也满足只取第一位元素的计算情况。
dp[1] = dp[0] && set.contains(s.substring(0, 1));
4.遍历顺序
i为正序遍历即可
5.程序
class Solution {
public boolean isSpell(String s, String[] words) {
Set<String> set = new HashSet<>();
for(String word : words) {
set.add(word);
}
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for(int i = 1; i <= s.length(); i++) {
for(int j = 0; j < i; j++) {
if(dp[j] && set.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}
回溯
**这道题的回溯法我想不借助全局变量返回结果。**在编写的过程中有遇到一个坑。
初版:
private boolean dfs(String s, Set<String> wordDict, int startIndex) {
if(startIndex == s.length()) {
return true;
}
for(int i = startIndex; i < s.length(); i++) {
String tmp = s.substring(startIndex, i + 1);
if(wordDict.contains(tmp)) {
// 坑
return dfs(s, wordDict, i + 1);
}
}
return false;
}
这里的坑就是,我直接将结果递归结果返回回去了,这样就会造成只会将第一次判定的结果返回,而不去探索后续结果。这里将直接返回递归函数 改成 判定条件,这样如果不符合条件还可以继续进行循环遍历。
修改后:
private boolean dfs(String s, Set<String> wordDict, int startIndex) {
if(startIndex == s.length()) {
return true;
}
for(int i = startIndex; i < s.length(); i++) {
String tmp = s.substring(startIndex, i + 1);
if(wordDict.contains(tmp) && dfs(s, wordDict, i + 1)) {
return true;
}
}
return false;
}
这样的递归会有很多重复判断,所有可以记录状态避免冗余的判断。
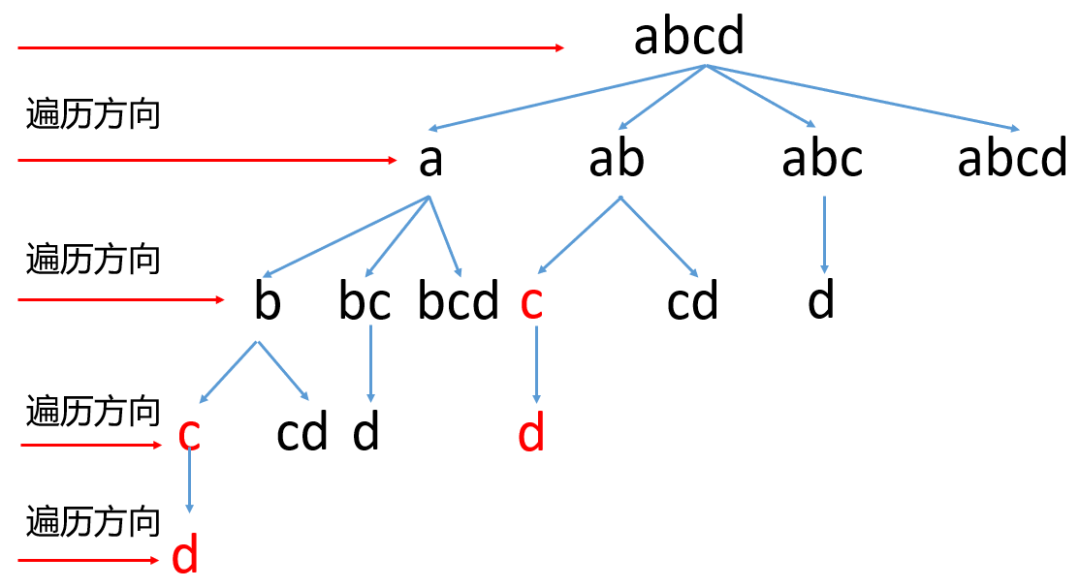
状态通过下标记录,若下标已经访问过了,则说明以此下标作为结尾的单词没能完成拼接。(若此前完成了拼接,就返回true了,就不会走到这一步了)
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> set = new HashSet<>();
Set<Integer> indexSet = new HashSet<>();
for(String word : wordDict) {
set.add(word);
}
return dfs(s, set, indexSet, 0);
}
private boolean dfs(String s, Set<String> wordDict, Set<Integer> indexSet, int startIndex) {
if(startIndex == s.length()) {
return true;
}
for(int i = startIndex; i < s.length(); i++) {
// 若状态此前已访问过,则说明失败了,直接跳过
if(indexSet.contains(i)) {
continue;
}
String tmp = s.substring(startIndex, i + 1);
// 当包含此词语时
if(wordDict.contains(tmp)) {
// 记录状态
indexSet.add(i);
// 判断递归结果,若结果失败会继续进行遍历判断
if(dfs(s, wordDict, indexSet, i + 1)) {
return true;
}
}
}
// 当前遍历都失败了,则返回失败
return false;
}
}

























 1022
1022











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








