歌单组合算法解析-CSDN博客

本文链接：https://blog.csdn.net/qq_40123329/article/details/85254271

牛客网题目链接：https://www.nowcoder.com/questionTerminal/f3ab6fe72af34b71a2fd1d83304cbbb3

小Q有X首长度为A的不同的歌和Y首长度为B的不同的歌，现在小Q想用这些歌组成一个总长度正好为K的歌单，每首歌最多只能在歌单中出现一次，在不考虑歌单内歌曲的先后顺序的情况下，请问有多少种组成歌单的方法。

输入描述:

每个输入包含一个测试用例。
每个测试用例的第一行包含一个整数，表示歌单的总长度K(1<=K<=1000)。
接下来的一行包含四个正整数，分别表示歌的第一种长度A(A<=10)和数量X(X<=100)以及歌的第二种长度B(B<=10)和数量Y(Y<=100)。保证A不等于B。

输出描述:

输出一个整数,表示组成歌单的方法取模。因为答案可能会很大,输出对1000000007取模的结果。

方法一

我们首先可以用数学的思维来解释。假设我们确定了x首A和y首B，即xA+yB=K

那接下来就是从X首A中无序选择x首A，再从Y首B中无序选择y首B的问题了。

xA+yB=K

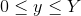
$0\leq x\leq X$ $0\leq y\leq Y$

那么所有解(x,y)的 $C_{X}^{x}\times C_{Y}^{y}$ 之和就是所有可能的方法的种数。

之后考虑如何计算 $C_{m}^{n}$

由排列组合的递推公式我们可知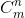： $C_{m}^{n}$ = $C_{m-1}^{n-1}$ + $C_{m-1}^{n}$ 。而这种递推表达式像极了杨辉三角。

因此我们可以构造c[m][n]=c[m-1][n-1]+c[m-1][n]

而其实杨辉三角的某一值c[i][j]的数值与从i个数值中随机选取j个数值的种数是一致的。

杨辉三角的构造

#include <stdio.h>

long long c[15][15];
void yang_hui()
{
    c[0][0]=1;
    for(int i=1;i<=14;i++)
    {
        c[i][0]=1;
        for(int j=1;j<=14;j++)
        {
            c[i][j]=c[i-1][j-1]+c[i-1][j];
        }
    }
}

int main()
{
    for(int i=0;i<=14;i++)
    {
        for(int j=0;j<=14;j++)
            {
                printf("%-7d",c[i][j])  #%-7d是左对齐  %7d是右对齐
            }
        printf("\n");
    }
}

该问题的解决代码如下

#include <stdio.h>

const int mod=100000007;
long long c[105][105];

void init()
{	
	c[0][0]=1;
	for(int i=1;i<=100;i++)
	{
		c[i][0]=1;
		for(int j=1;j<=100;j++)
		{
			c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
		}
	}
}

int main()
{
	int k,a,b,x,y;
	long long ans=0;
	init();
	scanf("%d",&k);
	scanf("%d%d%d%d",&a,&x,&b,&y);
	for(int i=0;i<=x;i++)
	{
		if(i*a<=k&&(k-a*i)%b==0&&(k-a*i)/b<=y)
			ans=(ans+(c[x][i]*c[y][(k-a*i)/b])%mod)%mod;
	}
	printf("%lld\n",ans);
	return 0;
}

方法二 01背包问题

01背包问题详解

戳这里

确实是全网最佳的。一开始搞不懂为啥当第i件物品的容量小于背包的容量时，把这个背包直接放进去不是最优解，而需要比较放于不放该物品的价值： V(i,j)=max｛ V(i-1,j)，V(i-1,j-w(i))+v(i) ｝

直到跟着过程自己搞一遍之后，才发现了问题。确实f(3,5)=f(2,5-4)+5=5<f(3,5)=f(2,5)=7

想了想终于发现，如果人脑来处理这个问题肯定1秒钟给出正确答案（前三个物品放入容量为5的背包里，当然放入前2个物品可以使背包价值最大）。

而当第i件物品的容量小于背包的容量时，把这个背包直接放进去，肯定不是明智的方法，很有可能出现背包容量没有充分利用的状态，所以要进行比较。对放与不放第i个背包进行比较。

背包九讲

戳这里

该问题解决代码

#include <iostream>
#include <cstring>

using namespace std;
 
int K, A, X, B, Y;
int dp[201][1001];
int p[201];
const int mod=1000000007;
 
int main()
{
    while(cin >> K)
    { 
        cin >> A >> X >> B >> Y; 
        memset(dp, 0, sizeof(dp));
        dp[0][0] = 1; 
        for(int i = 1; i <= X; i++) 
            p[i] = A; 
        for(int j = X + 1; j <= X + Y; j++) 
            p[j] = B; 
        for(int i = 1; i <= X + Y; i++) 
            for(int j = 0; j <= K; j++) 
            { 
                if(j >= p[i]) 
                    dp[i][j] = (dp[i - 1][j] % mod + dp[i - 1][j - p[i]] % mod) % mod; 
                else 
                    dp[i][j] = dp[i - 1][j] % mod; 
            } 
        cout << dp[X + Y][K] % mod << endl; 
    } 
}

其中dp[i][j]表示的是前i首歌曲组成长度为K歌单的方法数。

当组成歌单的长度j不小于第i首歌的长度时，可以有 dp[i][j] = (dp[i - 1][j] % mod + dp[i - 1][j - p[i]] % mod) % mod; 也就是说第前i首歌曲组成长度为K歌单的方法数等于前i-1首歌曲组成长度为K歌单的方法数加上前i-1首歌曲组成长度为j-p[i]歌单的方法数。（就是选与不选第i首歌曲的方法数之和）

当组成歌单的长度j小于第i首歌的长度时，第i首歌显然装不进去了。有dp[i][j] = dp[i - 1][j] % mod;