WORLD声码器:A Vocoder-Based High-Quality Speech Synthesis System for Real-Time Applications_world: a vocoder-based high-quality speech synthes-CSDN博客

附一个大佬的marlin讲解主页链接 http://shartoo.github.io/

abstract

可以实现实时、高质量的语音合成。比传统的系统速度快10倍以上，RTF(real time factor)表明它可以应用于实时系统。通过3个语音信号相关的参数合成语音–基频f0，谱包络spectrum envelope, 非周期信号参数aperiodic parameter。

1. introduction

两个要求：

高质量
实时性

高质量的语音合成系统包括基频F0和谱包络估计算法，以及参数估计的合成算法。之前的研究：STRAIGHT可以合成高质量的语音，对语音很容易进行操作。为了满足实时性，提出简化版–Real time STRAIGHT,但是大大削弱了语音质量。
WORLD声码器用3个算法提取3个参数，然后用一个合成算法把他们当作输入，可以实现高质量的语音合成。

2. overview of WORLD

图1是处理的过程

输入wave通过DIO算法估计出F0 contour（基频）
F0和wave作为输入，由cheap trick估计出spectral envelope(频谱包络）
输入F0/sp/wave，用PLATINUM将提取出来的信号进行估计，得到aperiodic parameter(非周期参数)。非周期参数的定义和之前的不一样。
WORLD不能和STRAIGHT的衍生系列一样操纵非周期参数，但是可以和它们一样操作F0和频率包络。

在这里插入图片描述

2.1 DIO: F0估计算法

F0是周期信号的最长持续时间的倒数（基频会产生二次谐波，三次谐波，周期是基频的整数分之一，最长的周期是基频的持续周期，所以理论上会对应频率最低的部分，在语谱图上对应最下边的亮线，频率能量最高的部分），提出很多算法以估计F0；它有两种特性：一个是时域特征，比如自相关，一个是频域特征，比如倒谱ceph。
WORLD用DIO估计F0，比YIN、SWIPE要快，但是性能依然很好。DIO分为三步：
1⃣️不同频带的低通滤波器：因为不知道F0的基频，所以这一步包含不同周期的sin低通滤波器；
2⃣️计算得到各个可能的F0的可靠性，因为由基波分量组成的sin信号包含四个间隔（两个顶点、两个过零点），如图2所示。如果滤波器得到的间隔长度是一致的，说明是同一个基波。
3⃣️选出置信度最高的基波。
在这里插入图片描述

2.2 CheapTrick: Spectral Envelope Estimation Algorithm

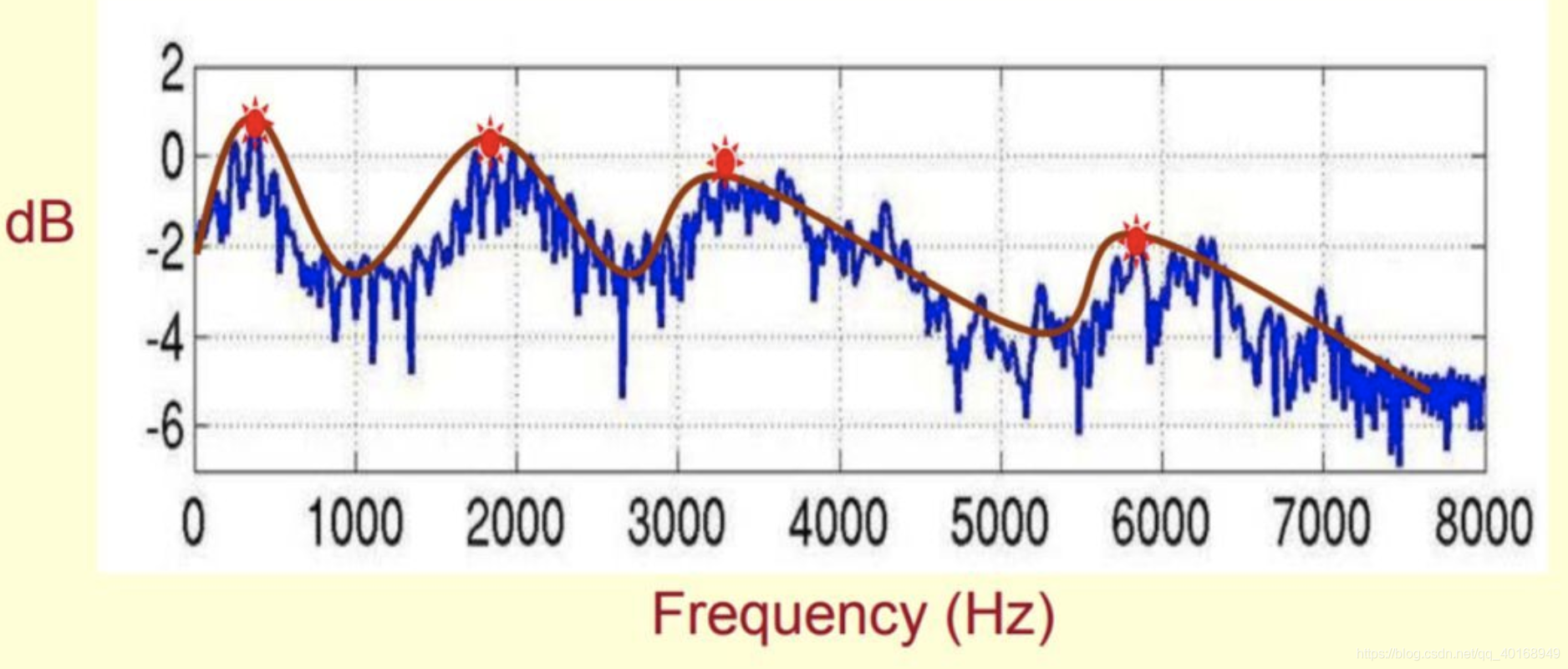
谱包络也是一个重要的参数，如下图所示，是指在频率-振幅图中，用平滑的曲线将所有共振峰连接起来，这个平滑的曲线就是谱包络。预测它的典型算法有cepstrum和LPC（linear predictive coding)。难度在于估计的结果取决于the temporal position，很难消除它的影响。
WORLD用CheapTrick去做谱分析，它的思想来源于pitch synchronous analysis （音高同步分析），使用长度为3T0的hanning window。
在这里插入图片描述

首先计算窗口波形下的谱能量，对它窗口下的总能量按照公式（1）进行时域稳定。
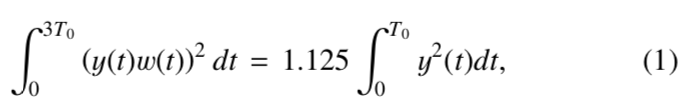
然后用rectangular window对（1）得到的功率谱进行平滑，求得单个周期能量w0=2pai/T0

最后，进行specialized liftering
ps是功率谱pw的倒谱，

倒谱（cepstrum)：一种信号的傅里叶变换谱经过对数运算后再进行傅里叶反变换。由于一般傅里叶谱是复数谱，因而又称复倒谱。
在这里插入图片描述

2.3 PLATINUM：提取非周期参数

mixed excitation和aperiodicity经常用在合成中。在Legacy-STRAIGHT 和 TANDEM-STRAIGHT中，aperiodicity被用于合成周期和非周期的信号。WORLD则直接用从波形、F0、和谱包络中得到的mixed excitation—PLATINUM。
PLATINUM 窗长2T，窗函数 $X (w)$ 被最小的相谱分割。相谱 $S m （ w ）$ 可以计算为
在这里插入图片描述
提取的excitation function可以表示为

在PLATINUM中，每一个声带振动相关的temporal position（？？）必须确定，它是由F0和波形共同决定的。步骤是：（1）确定出有声的部分；（2）确定这个部分时间上的中心位置ta；（3）时间间隔ta±T0，在这个区间的temporal position有最大值y(t)²，将这个数值定义为最大值，一旦初始值被确定，基于声码器的合成算法自动计算其他的vocal position(声带位置），定义为基于F0 contour脉冲响应的起源。这个过程在每一个有声段都被重复执行。

2.4 Synthesis Algorithm

Legacy-STRAIGHT and TANDEM-STRAIGHT依靠周期和非周期的response计算声带振动，TANDEM-STRAIGHT直接用周期响应，Legacy-STRAIGHT操纵group delay以避免嗡嗡声。
在WORLD中，声带的振动是基于最小相位响应和激励信号上计算的。从图3可以看出，WORLD比STRAIGHT的卷积要少，因此计算力的需求更少。F0被用于决定每一个声带振动的初始时间位置。
在这里插入图片描述
图4说明了WORLD和STRAIGHT从输入语音提取激励信号，并且合成语音的过程。最上边是输入的wav，中间是卷积之前的激励信号；下边是合成的wav。因为Legacy 和TANDEM的激励信号不仅取决于谱包络，也取决于非周期性，它从拉平的谱包络中计算。

2.5 implementation

作者的网站上可以获得C语言版和matlab版的代码实现，但是最新的Legacy-STRAIGHT只有matlab版，为了公平比较，下文都用matlab进行对比。

3. evaluation

所有系统都对用户可以设定的参数进行了优化，使其在特定情况下的性能更好；但是为了真是比较各个系统真正的合成性能，我们用的都是没有优化的系统。
WORLD的执行命令如下:x–input waveform; fs采样率； f0基频，最后合成的时候只用到f0和spec
在这里插入图片描述
&dmsp;TANDEM-STRAIGHT的执行命令：第1步提取的基频会在后续步进行优化，source表示f0和非周期信息（ap)，

legacy-STRAIGHT,f0和ap的信息在同一步里边提取，

3.2 Characteristics of Speech Used in the Evaluation

用带有浊辅音的speech进行测试，之前的测试基本都只有元音，图5说明了F0的范围，基本都是100-300hz.
在这里插入图片描述

3.3 Subjective Evaluation of Sound Quality

基于MUSHRA做的测试，至少要给一个piece100分，分5个等级。
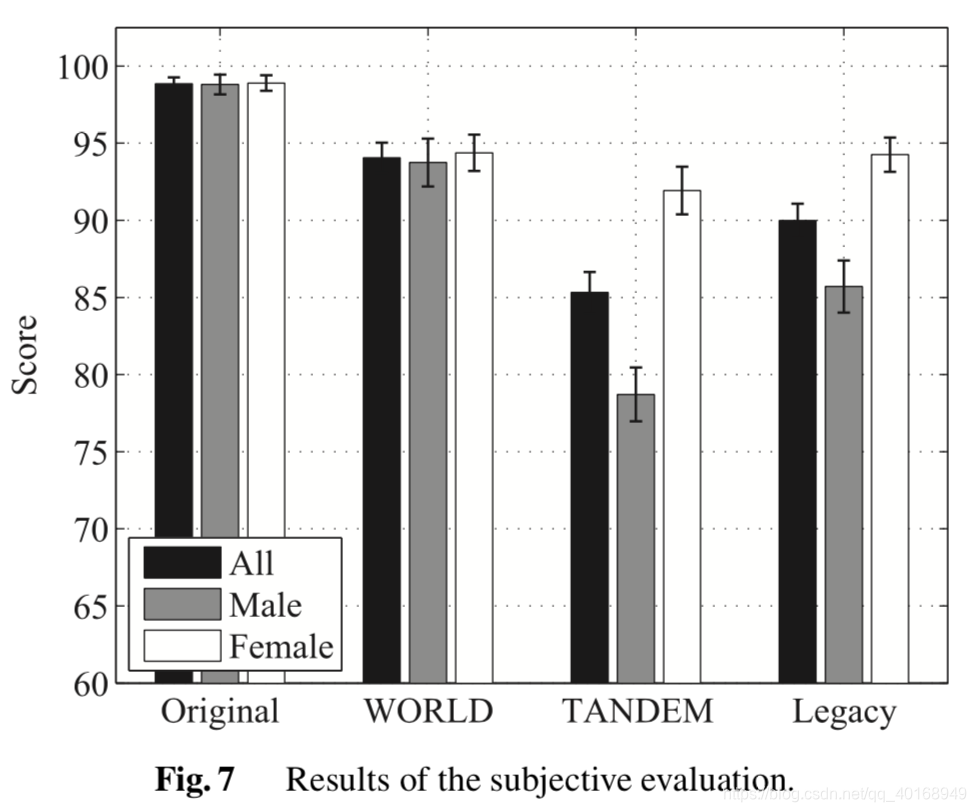
图7是测试结果，在女声上区别不大，WORLD和legacy非常接近；但是在男声上，WORLD要明显优于其他的系统。
在这里插入图片描述

3.4 Evaluation of Processing Speed

WORLD明显优于其他的，legacy主要加速了F0的处理速度（但是增大了sp的估计时间）。
在这里插入图片描述

4. discussion

4.1 Sound Quality of Synthesized Speech

world需要输入的语音帧有比较高的信噪比，如果有噪声的话很难合成高质量的语音。而且vuv（voice unvoice）的估计准确率也会很大程度影响语音的质量。改进目标–增强噪声鲁棒性。
WORLD和原始语音在音素的边界有区别，WORLD和其他系统的区别不仅在于音素边界，也在合成的元音质量；TANDEM-STRAIGHT比其他系统合成的男声元音差很多，主要是因为合成语音相位的区别。相比于high F0的系统，在low F0中人们可以更容易察觉到语音相位的不同，说明在low-pitch speech中使用最小相位是不合适的。Legacy-STRAIGHT中使用group delay manipulation改善low-pitch的语音质量，这也是legacy和TANDEM合成质量区别的一个原因。已经证明相位对于语音质量是有影响的，这也是WORLD下一步改进的目标。

4.2 Processing Speed

WORLD比其他的系统处理速度快很多，主要在（1）其他系统对每一帧做STFT，计算密集，WORLD使用DIO算法对整个wav滤波，计算过零间隔，速度快很多；（2）其他系统用两个系统估计sp，cheaptrick只需要一个；（3）估计ap的时候，WORLD没有post-preprocessing;（4）合成的时候， WORLD做一个简单的卷积就可以实现。
进一步提速的方式，改写matlab代码为C，换CPU到GPU。

WORLD提取到的是187维特征

0-59	60-119	120-179	180	181	182	183	184	185	186
60	60	60	1	1	1	1	1	1	1
mgc	△mgc	△△mgc	uvu	lnf0	△lnf0	△△lnf0	ln bap	△ln bap	△△ln bap

△表示后一帧与前一帧求一阶差分
△△表示后一帧与前一帧求2阶差分
目的是平滑处理
p.s.单独用make之后得到的analysis命令，16khz语音提取到的ap是一阶，44khz提取到的ap是5阶
对于 $f (x)$ ，一阶差分 $\delta_n=f(x_{n})-f(x_{n-1})$
二阶差分 $\delta\delta_n=\delta_{n}-\delta_{n-1}$