回溯算法 组合问题

class Solution {
    private List<List<Integer>> ans = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        getCombine(n, k, 1, new ArrayList<>());
        return ans;
    }
    
    public void getCombine(int n, int k, int start, List<Integer> list) {
        if(k == 0) {
            ans.add(new ArrayList<>(list));    //这里直接用list不行  直接add（list）输出全是[]
            return;
        }
        for(int i = start;i <= n - k + 1;i++) {  //注意起点，每次循环，新的getCombine起点要从i开始，而不是start+1
            list.add(i);
            getCombine(n, k - 1, i+1, list);
            list.remove(list.size() - 1);  //为什么要删除呢？ 删除的目的是将本层加入的数据移除
        }
    }
}

class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<Integer> a = new ArrayList<>();
        getsum(candidates,target,0,a);
        return ans;
    }
    public void getsum(int[] candidates, int target, int start, List<Integer> list){
        int len = candidates.length;
        if(target < 0){
            return ;
        }
        if(target == 0){
            ans.add(new ArrayList<>(list));    
        }
        for(int i=start; i<len; i++){
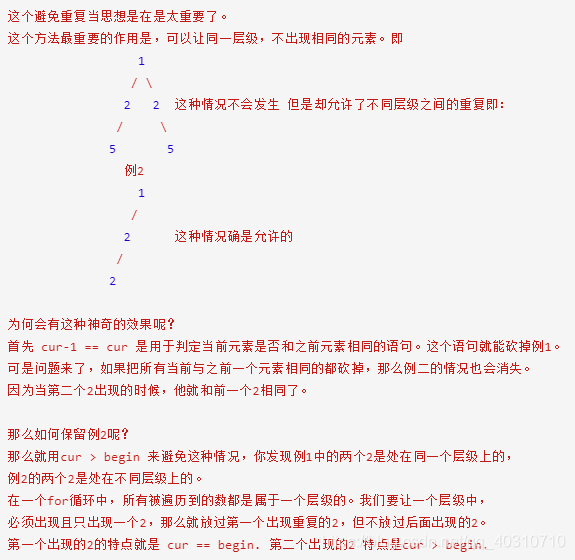
            if(i>start&&candidates[i]==candidates[i-1]){    //这句话至关重要，去重操作
                continue;
            }
            list.add(candidates[i]);
            getsum(candidates,target-candidates[i],i+1,list);
            list.remove(list.size()-1);
        }
    }
}

动态规划思路  
状态转移方程：dp[i]= dp[i - nums[0]] + dp[i - nums[1]] + dp[i - nums[2]] + ... （当 [] 里面的数 >= 0）
public class Solution {

    /**
     * 这里状态定义就是题目要求的，并不难，状态转移方程要动点脑子，也不难：
     * 状态转移方程：dp[i]= dp[i - nums[0]] + dp[i - nums[1]] + dp[i - nums[2]] + ... （当 [] 里面的数 >= 0）
     * 特别注意：dp[0] = 1，表示，如果那个硬币的面值刚刚好等于需要凑出的价值，这个就成为 1 种组合方案
     * 再举一个具体的例子：nums=[1, 3, 4], target=7;
     * dp[7] = dp[6] + dp[4] + dp[3]
     * 即：7 的组合数可以由三部分组成，1 和 dp[6]，3 和 dp[4], 4 和dp[3];
     *
     * @param nums
     * @param target
     * @return
     */
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        // 这个值被其它状态参考，设置为 1 是合理的
        dp[0] = 1;

        for (int i = 1; i <= target; i++) {
            for (int num : nums) {
                if (num <= i) {
                    dp[i] += dp[i - num];
                }
            }
        }
        return dp[target];
    }
}

生成括号

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ret = new ArrayList<String>();
        StringBuilder ans = new StringBuilder();
        int left = n;
        int right = n;
        get(left,right,ans,ret);
        return ret;
        
    }
    public void get(int left, int right, StringBuilder ans,List<String> ret){
        if(left==0&&right==0){
            ret.add(ans.toString());
            return;
        }
        if(left>0){
            ans.append('(');
            get(left-1,right, ans, ret);
            ans.deleteCharAt(ans.length()-1);
        }
        if(right>left){
            ans.append(')');
            get(left,right-1, ans, ret);
            ans.deleteCharAt(ans.length()-1);
        }
        
    }
}

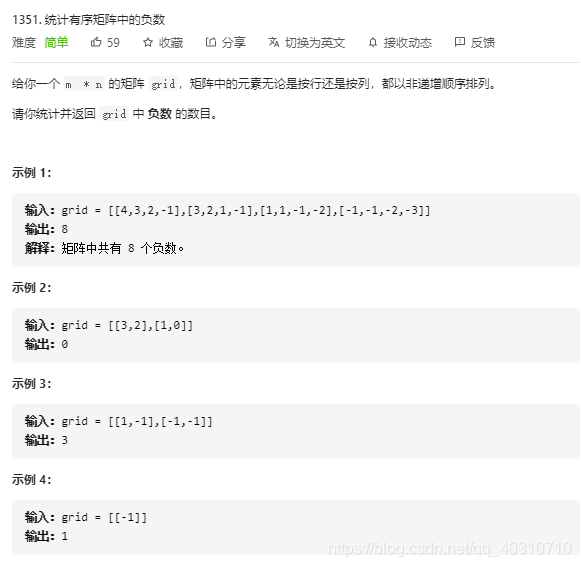
class Solution {
    public int countNegatives(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int count = 0;
        for(int i=0; i<row; i++){
            for(int j=0; j<col; j++){
                if(grid[i][j]<0){
                    count = count + col - j;
                    break;
                }
            }
        }
        return count;
    }
}