零基础入门数据挖掘-Task2 数据分析
本文为参加数据挖掘比赛第二阶段的心得分享。
Datawhale 二手车数据挖掘-Task2数据分析
一、 EDA-Exploratory Data Analysis-数据探索性分析
任务目标:
EDA的价值主要在于熟悉数据集,了解数据集,对数据集进行验证来确定所获得数据集可以用于接下来的机器学习或者深度学习使用。
当了解了数据集之后我们下一步就是要去了解变量间的相互关系以及变量与预测值之间的存在关系。
引导数据科学从业者进行数据处理以及特征工程的步骤,使数据集的结构和特征集让接下来的预测问题更加可靠。
完成对于数据的探索性分析,并对于数据进行一些图表或者文字总结并打卡。
二、 相关任务
1.载入各种数据科学以及可视化库:
数据科学库 pandas、numpy、scipy;
可视化库 matplotlib、seabon;其他;
2.载入数据:
载入训练集和测试集;
简略观察数据(head()+shape);
3.数据总览:
通过describe()来熟悉数据的相关统计量
通过info()来熟悉数据类型
4.判断数据缺失和异常
查看每列的存在nan情况
异常值检测
5.了解预测值的分布
总体分布概况(无界约翰逊分布等)
查看skewness and kurtosis
查看预测值的具体频数
6.特征分为类别特征和数字特征,并对类别特征查看unique分布
7.数字特征分析
相关性分析
查看几个特征得 偏度和峰值
每个数字特征得分布可视化
数字特征相互之间的关系可视化
多变量互相回归关系可视化
8.类型特征分析
unique分布
类别特征箱形图可视化
类别特征的小提琴图可视化
类别特征的柱形图可视化类别
特征的每个类别频数可视化(count_plot)
9.用pandas_profiling生成数据报告
三、 对应代码实现
1.载入各种数据科学以及可视化库: 数据科学库 pandas、numpy、scipy; 可视化库 matplotlib、seabon;其他;#coding:utf-8
#导入warnings包,利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
2.载入数据:
##载入训练集和测试集;
##简略观察数据(head()+shape);
## 1) 载入训练集和测试集;
Train_data = pd.read_csv('data/car_train_0110.csv', sep=' ')
Test_data = pd.read_csv('data/car_testA_0110.csv', sep=' ')
输出首尾5行,对于观察数据的大概特征很方便
## 2) 简略观察数据(head()+shape)
Train_data.head().append(Train_data.tail())
| SaleID | name | regDate | model | brand | bodyType | fuelType | gearbox | power | kilometer | ... | v_14 | v_15 | v_16 | v_17 | v_18 | v_19 | v_20 | v_21 | v_22 | v_23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 134890 | 734 | 20160002 | 13.0 | 9 | NaN | 0.0 | 1.0 | 0 | 15.0 | ... | 0.092139 | 0.000000 | 18.763832 | -1.512063 | -1.008718 | -12.100623 | -0.947052 | 9.077297 | 0.581214 | 3.945923 |
| 1 | 306648 | 196973 | 20080307 | 72.0 | 9 | 7.0 | 5.0 | 1.0 | 173 | 15.0 | ... | 0.001070 | 0.122335 | -5.685612 | -0.489963 | -2.223693 | -0.226865 | -0.658246 | -3.949621 | 4.593618 | -1.145653 |
| 2 | 340675 | 25347 | 20020312 | 18.0 | 12 | 3.0 | 0.0 | 1.0 | 50 | 12.5 | ... | 0.064410 | 0.003345 | -3.295700 | 1.816499 | 3.554439 | -0.683675 | 0.971495 | 2.625318 | -0.851922 | -1.246135 |
| 3 | 57332 | 5382 | 20000611 | 38.0 | 8 | 7.0 | 0.0 | 1.0 | 54 | 15.0 | ... | 0.069231 | 0.000000 | -3.405521 | 1.497826 | 4.782636 | 0.039101 | 1.227646 | 3.040629 | -0.801854 | -1.251894 |
| 4 | 265235 | 173174 | 20030109 | 87.0 | 0 | 5.0 | 5.0 | 1.0 | 131 | 3.0 | ... | 0.000099 | 0.001655 | -4.475429 | 0.124138 | 1.364567 | -0.319848 | -1.131568 | -3.303424 | -1.998466 | -1.279368 |
| 249995 | 10556 | 9332 | 20170003 | 13.0 | 9 | NaN | NaN | 1.0 | 58 | 15.0 | ... | 0.079119 | 0.001447 | 11.782508 | 20.402576 | -2.722772 | 0.462388 | -4.429385 | 7.883413 | 0.698405 | -1.082013 |
| 249996 | 146710 | 102110 | 20030511 | 29.0 | 17 | 3.0 | 0.0 | 0.0 | 61 | 15.0 | ... | 0.000000 | 0.002342 | -2.988272 | 1.500532 | 3.502201 | -0.761715 | -2.484556 | -2.532968 | -0.940266 | -1.106426 |
| 249997 | 116066 | 82802 | 20130312 | 124.0 | 16 | 6.0 | 0.0 | 1.0 | 122 | 3.0 | ... | 0.003358 | 0.100760 | -6.939560 | -1.144959 | -5.337949 | 0.896026 | -0.592565 | -3.872725 | 2.135984 | 3.807554 |
| 249998 | 90082 | 65971 | 20121212 | 111.0 | 4 | 7.0 | 5.0 | 0.0 | 184 | 9.0 | ... | 0.002974 | 0.008251 | -7.222167 | -1.383696 | -5.402794 | -0.409451 | -1.891556 | -3.104789 | -3.777374 | 3.186218 |
| 249999 | 76453 | 56954 | 20051111 | 13.0 | 9 | 3.0 | 0.0 | 1.0 | 58 | 12.5 | ... | 0.000000 | 0.009071 | 10.491312 | -11.270043 | -0.272595 | -0.026478 | -2.168249 | -0.980042 | -0.955164 | -1.169593 |
10 rows × 40 columns
Test_data.shape
(50000, 39)
3.数据总览:
通过describe()来熟悉数据的相关统计量
describe种有每列的统计量,个数count、平均值mean、方差std、最小值min、中位数25% 50% 75% 、以及最大值 看这个信息主要是瞬间掌握数据的大概的范围以及每个值的异常值的判断,比如有的时候会发现999 9999 -1 等值这些其实都是nan的另外一种表达方式,有的时候需要注意下
## 1) 通过describe()来熟悉数据的相关统计量
Train_data.describe()
| SaleID | name | regDate | model | brand | bodyType | fuelType | gearbox | power | kilometer | ... | v_14 | v_15 | v_16 | v_17 | v_18 | v_19 | v_20 | v_21 | v_22 | v_23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 250000.000000 | 250000.000000 | 2.500000e+05 | 250000.000000 | 250000.000000 | 224620.000000 | 227510.000000 | 236487.000000 | 250000.000000 | 250000.000000 | ... | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 | 250000.000000 |
| mean | 185351.790768 | 83153.362172 | 2.003401e+07 | 44.911480 | 7.785236 | 4.563271 | 1.665008 | 0.780783 | 115.528412 | 12.577418 | ... | 0.032489 | 0.030408 | 0.014725 | 0.000915 | 0.006273 | 0.006604 | -0.001374 | 0.000609 | -0.004025 | 0.001834 |
| std | 107121.188763 | 72540.799964 | 7.770250e+04 | 50.640081 | 7.694010 | 1.912515 | 2.339646 | 0.413717 | 196.141828 | 3.990632 | ... | 0.038792 | 0.049333 | 8.779163 | 5.771081 | 4.880981 | 4.124722 | 3.803626 | 3.555353 | 2.864713 | 2.323680 |
| min | 1.000000 | 0.000000 | 1.910000e+07 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.500000 | ... | 0.000000 | 0.000000 | -10.412444 | -15.538236 | -21.009214 | -13.989955 | -9.599285 | -11.181255 | -7.671327 | -2.350888 |
| 25% | 92501.750000 | 14500.000000 | 1.999061e+07 | 6.000000 | 1.000000 | 3.000000 | 0.000000 | 1.000000 | 70.000000 | 12.500000 | ... | 0.000129 | 0.000000 | -5.552269 | -0.901181 | -3.150385 | -0.478173 | -1.727237 | -3.067073 | -2.092178 | -1.402804 |
| 50% | 185264.500000 | 65314.500000 | 2.003111e+07 | 27.000000 | 6.000000 | 4.000000 | 0.000000 | 1.000000 | 105.000000 | 15.000000 | ... | 0.001961 | 0.002567 | -3.821770 | 0.223181 | -0.058502 | 0.038427 | -0.995044 | -0.880587 | -1.199807 | -1.145588 |
| 75% | 278128.500000 | 143761.250000 | 2.008081e+07 | 70.000000 | 11.000000 | 7.000000 | 5.000000 | 1.000000 | 150.000000 | 15.000000 | ... | 0.075672 | 0.056568 | 3.599747 | 1.263737 | 2.800475 | 0.569198 | 1.563382 | 3.269987 | 2.737614 | 0.044865 |
| max | 370946.000000 | 233044.000000 | 2.019121e+07 | 250.000000 | 39.000000 | 7.000000 | 6.000000 | 1.000000 | 20000.000000 | 15.000000 | ... | 0.130785 | 0.184340 | 36.756878 | 26.134561 | 23.055660 | 16.576027 | 20.324572 | 14.039422 | 8.764597 | 8.574730 |
8 rows × 40 columns
通过info()来熟悉数据类型
## 2) 通过info()来熟悉数据类型
Train_data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 250000 entries, 0 to 249999
Data columns (total 40 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 SaleID 250000 non-null int64
1 name 250000 non-null int64
2 regDate 250000 non-null int64
3 model 250000 non-null float64
4 brand 250000 non-null int64
5 bodyType 224620 non-null float64
6 fuelType 227510 non-null float64
7 gearbox 236487 non-null float64
8 power 250000 non-null int64
9 kilometer 250000 non-null float64
10 notRepairedDamage 201464 non-null float64
11 regionCode 250000 non-null int64
12 seller 250000 non-null int64
13 offerType 250000 non-null int64
14 creatDate 250000 non-null int64
15 price 250000 non-null int64
16 v_0 250000 non-null float64
17 v_1 250000 non-null float64
18 v_2 250000 non-null float64
19 v_3 250000 non-null float64
20 v_4 250000 non-null float64
21 v_5 250000 non-null float64
22 v_6 250000 non-null float64
23 v_7 250000 non-null float64
24 v_8 250000 non-null float64
25 v_9 250000 non-null float64
26 v_10 250000 non-null float64
27 v_11 250000 non-null float64
28 v_12 250000 non-null float64
29 v_13 250000 non-null float64
30 v_14 250000 non-null float64
31 v_15 250000 non-null float64
32 v_16 250000 non-null float64
33 v_17 250000 non-null float64
34 v_18 250000 non-null float64
35 v_19 250000 non-null float64
36 v_20 250000 non-null float64
37 v_21 250000 non-null float64
38 v_22 250000 non-null float64
39 v_23 250000 non-null float64
dtypes: float64(30), int64(10)
memory usage: 76.3 MB
4.判断数据缺失和异常
查看每列的存在nan情况
异常值检测
## 1) 查看每列的存在nan情况
Train_data.isnull().sum()
SaleID 0
name 0
regDate 0
model 0
brand 0
bodyType 25380
fuelType 22490
gearbox 13513
power 0
kilometer 0
notRepairedDamage 48536
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
v_15 0
v_16 0
v_17 0
v_18 0
v_19 0
v_20 0
v_21 0
v_22 0
v_23 0
dtype: int64
Test_data.isnull().sum()
SaleID 0
name 0
regDate 0
model 0
brand 0
bodyType 5110
fuelType 4402
gearbox 2713
power 0
kilometer 0
notRepairedDamage 9628
regionCode 0
seller 0
offerType 0
creatDate 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
v_15 0
v_16 0
v_17 0
v_18 0
v_19 0
v_20 0
v_21 0
v_22 0
v_23 0
dtype: int64
# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()

通过以上两句可以很直观的了解哪些列存在 “nan”, 并可以把nan的个数打印,主要的目的在于 nan存在的个数是否真的很大,如果很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉
# 可视化看下缺省值
msno.matrix(Train_data.sample(250))

msno.bar(Train_data.sample(1000))

# 可视化看下缺省值
msno.matrix(Test_data.sample(250))

msno.bar(Test_data.sample(1000))

## 2) 查看异常值检测
Train_data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 250000 entries, 0 to 249999
Data columns (total 40 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 SaleID 250000 non-null int64
1 name 250000 non-null int64
2 regDate 250000 non-null int64
3 model 250000 non-null float64
4 brand 250000 non-null int64
5 bodyType 224620 non-null float64
6 fuelType 227510 non-null float64
7 gearbox 236487 non-null float64
8 power 250000 non-null int64
9 kilometer 250000 non-null float64
10 notRepairedDamage 201464 non-null float64
11 regionCode 250000 non-null int64
12 seller 250000 non-null int64
13 offerType 250000 non-null int64
14 creatDate 250000 non-null int64
15 price 250000 non-null int64
16 v_0 250000 non-null float64
17 v_1 250000 non-null float64
18 v_2 250000 non-null float64
19 v_3 250000 non-null float64
20 v_4 250000 non-null float64
21 v_5 250000 non-null float64
22 v_6 250000 non-null float64
23 v_7 250000 non-null float64
24 v_8 250000 non-null float64
25 v_9 250000 non-null float64
26 v_10 250000 non-null float64
27 v_11 250000 non-null float64
28 v_12 250000 non-null float64
29 v_13 250000 non-null float64
30 v_14 250000 non-null float64
31 v_15 250000 non-null float64
32 v_16 250000 non-null float64
33 v_17 250000 non-null float64
34 v_18 250000 non-null float64
35 v_19 250000 non-null float64
36 v_20 250000 non-null float64
37 v_21 250000 non-null float64
38 v_22 250000 non-null float64
39 v_23 250000 non-null float64
dtypes: float64(30), int64(10)
memory usage: 76.3 MB
Train_data['notRepairedDamage'].value_counts()
1.0 176922
0.0 24542
Name: notRepairedDamage, dtype: int64
此数据集中的数据类型都是正常数字类型,符合处理标准
Train_data.isnull().sum()
SaleID 0
name 0
regDate 0
model 0
brand 0
bodyType 25380
fuelType 22490
gearbox 13513
power 0
kilometer 0
notRepairedDamage 48536
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
v_15 0
v_16 0
v_17 0
v_18 0
v_19 0
v_20 0
v_21 0
v_22 0
v_23 0
dtype: int64
下一步寻找倾斜严重的,这类数据一般对预测没什么帮助,可以先做删除处理
Train_data["seller"].value_counts()
1 249999
0 1
Name: seller, dtype: int64
Train_data["offerType"].value_counts()
0 249991
1 9
Name: offerType, dtype: int64
del Train_data["seller"]
del Train_data["offerType"]
del Test_data["seller"]
del Test_data["offerType"]
5.了解预测值的分布
总体分布概况(无界约翰逊分布等)
查看skewness and kurtosis
查看预测值的具体频数
Train_data['price']
0 520
1 5500
2 1100
3 1200
4 3300
...
249995 1200
249996 1200
249997 16500
249998 31950
249999 1990
Name: price, Length: 250000, dtype: int64
Train_data['price'].value_counts()
0 7312
500 3815
1500 3587
1000 3149
1200 3071
...
11320 1
7230 1
11448 1
9529 1
8188 1
Name: price, Length: 4585, dtype: int64
## 1) 总体分布概况(无界约翰逊分布等)
import scipy.stats as st
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
在这里插入图片描述

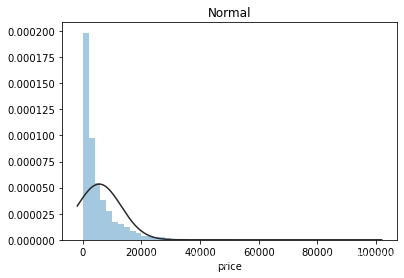

通过上面三幅图片,可以看出价格不服从正态分布,所以在进行回归之前,它必须进行转换。虽然对数变换做得很好,但最佳拟合是无界约翰逊分布
## 2) 查看skewness and kurtosis
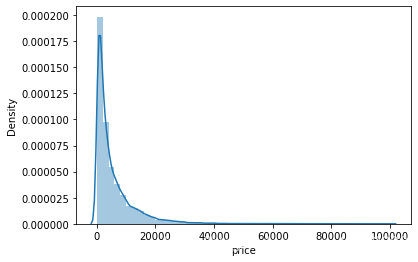
sns.distplot(Train_data['price']);
print("Skewness: %f" % Train_data['price'].skew())
print("Kurtosis: %f" % Train_data['price'].kurt())
Skewness: 3.535346
Kurtosis: 21.230678
Train_data.skew(), Train_data.kurt()
(SaleID 0.001712
name 0.513079
regDate -1.540844
model 1.499765
brand 1.314846
bodyType -0.070459
fuelType 0.701802
gearbox -1.357379
power 58.590829
kilometer -1.557472
notRepairedDamage -2.312519
regionCode 0.690405
creatDate -95.428563
price 3.535346
v_0 -1.504738
v_1 1.582428
v_2 1.198679
v_3 1.352193
v_4 0.217941
v_5 2.052749
v_6 0.090718
v_7 0.823610
v_8 -1.532964
v_9 1.529931
v_10 -2.584452
v_11 -0.906428
v_12 -2.842834
v_13 -3.869655
v_14 0.491706
v_15 1.308716
v_16 1.662893
v_17 0.233318
v_18 0.814453
v_19 0.100073
v_20 2.001253
v_21 0.180020
v_22 0.819133
v_23 1.357847
dtype: float64,
SaleID -1.201476
name -1.084474
regDate 11.041006
model 1.741896
brand 1.814245
bodyType -1.070358
fuelType -1.495782
gearbox -0.157525
power 4473.885260
kilometer 1.250933
notRepairedDamage 3.347777
regionCode -0.352973
creatDate 11376.694263
price 21.230678
v_0 2.901641
v_1 1.098703
v_2 3.749872
v_3 4.294578
v_4 6.953348
v_5 6.489791
v_6 -0.564878
v_7 -0.729838
v_8 0.370812
v_9 0.377943
v_10 4.796855
v_11 1.547812
v_12 6.136342
v_13 13.199575
v_14 -1.597532
v_15 -0.029594
v_16 2.240928
v_17 2.569341
v_18 2.967738
v_19 6.923953
v_20 6.852809
v_21 -0.759948
v_22 -0.741708
v_23 0.143713
dtype: float64)
通过上述偏度峰度的分析,creatData数据具有极不平衡的特性,通过它的分布密度图片来看,数据具有极不平衡的特性,有些信息效果不好
sns.distplot(Train_data['price']);

Train_data['creatDate'].value_counts()
20160403 9758
20160404 9521
20160320 9176
20160312 8946
20160321 8895
...
20150618 1
20160114 1
20160201 1
20150611 1
20140310 1
Name: creatDate, Length: 107, dtype: int64
sns.distplot(Train_data.skew(),color='blue',axlabel ='Skewness')

sns.distplot(Train_data.kurt(),color='orange',axlabel ='Kurtness')

## 3) 查看预测值的具体频数
plt.hist(Train_data['price'], orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()

Train_data['price'] = np.maximum(Train_data['price'],0.1)
## log变换 z之后的分布较均匀,可以进行log变换进行预测,这也是预测问题常用的trick
plt.hist(np.log(Train_data['price']), orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()

## 删除条件行的操作
Train_data1 = Train_data.drop(Train_data.index[Train_data['price'] <= 1])
## log变换 z之后的分布较均匀,可以进行log变换进行预测,这也是预测问题常用的trick
plt.hist(np.log(Train_data1['price']), orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()

Train_data1.shape
(241897, 38)
通过这个频数图,可知已有的二手车训练集数据中售价超过两万的比例很低,因此这部分的信息价值并不高,预测的准确性会更差。
6.特征分为类别特征和数字特征,并对类别特征查看unique分布
# 分离label即预测值
Y_train = Train_data['price']
# 数字特征
numeric_features = Train_data.select_dtypes(include=[np.number])
numeric_features.columns
# # 类型特征
# categorical_features = Train_data.select_dtypes(include=[np.object])
# categorical_features.columns
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]
# 特征nunique分布
for cat_fea in categorical_features:
print(cat_fea + "的特征分布如下:")
print("{}特征有个{}不同的值".format(cat_fea, Train_data[cat_fea].nunique()))
print(Train_data[cat_fea].value_counts())
name的特征分布如下:
name特征有个164312不同的值
451 452
73 429
1791 428
821 391
243 346
...
92419 1
88325 1
82182 1
84231 1
157427 1
Name: name, Length: 164312, dtype: int64
model的特征分布如下:
model特征有个251不同的值
0.0 20344
6.0 17741
4.0 13837
1.0 13634
12.0 8841
...
226.0 5
245.0 5
243.0 4
249.0 4
250.0 1
Name: model, Length: 251, dtype: int64
brand的特征分布如下:
brand特征有个40不同的值
0 53699
4 27109
11 26944
10 23762
1 22144
6 17202
9 12210
5 7343
15 6500
12 4704
7 3839
3 3831
17 3543
13 3502
8 3374
28 3161
19 2561
18 2451
16 2274
22 2264
23 2088
14 1892
24 1678
25 1611
20 1610
27 1392
29 1259
34 963
30 604
2 570
31 540
21 522
38 516
35 415
32 406
36 377
33 368
37 324
26 307
39 141
Name: brand, dtype: int64
bodyType的特征分布如下:
bodyType特征有个8不同的值
7.0 64571
3.0 53858
4.0 45646
5.0 20343
6.0 15290
2.0 12755
1.0 9882
0.0 2275
Name: bodyType, dtype: int64
fuelType的特征分布如下:
fuelType特征有个7不同的值
0.0 150664
5.0 72494
4.0 3577
3.0 385
2.0 183
1.0 147
6.0 60
Name: fuelType, dtype: int64
gearbox的特征分布如下:
gearbox特征有个2不同的值
1.0 184645
0.0 51842
Name: gearbox, dtype: int64
notRepairedDamage的特征分布如下:
notRepairedDamage特征有个2不同的值
1.0 176922
0.0 24542
Name: notRepairedDamage, dtype: int64
regionCode的特征分布如下:
regionCode特征有个8081不同的值
487 550
868 424
149 236
539 227
32 216
...
7959 1
8002 1
6715 1
7117 1
4144 1
Name: regionCode, Length: 8081, dtype: int64
# 特征nunique分布
for cat_fea in categorical_features:
print(cat_fea + "的特征分布如下:")
print("{}特征有个{}不同的值".format(cat_fea, Test_data[cat_fea].nunique()))
print(Test_data[cat_fea].value_counts())
name的特征分布如下:
name特征有个38668不同的值
73 98
821 89
243 77
451 74
826 73
..
106879 1
108926 1
176509 1
178556 1
67583 1
Name: name, Length: 38668, dtype: int64
model的特征分布如下:
model特征有个249不同的值
0.0 3916
6.0 3496
1.0 2806
4.0 2802
12.0 1745
...
247.0 2
246.0 2
214.0 1
243.0 1
232.0 1
Name: model, Length: 249, dtype: int64
brand的特征分布如下:
brand特征有个40不同的值
0 10697
4 5464
11 5374
10 4747
1 4390
6 3496
9 2408
5 1534
15 1325
12 929
7 782
3 736
17 732
13 679
8 666
28 645
19 534
18 487
16 458
22 430
14 416
23 397
24 390
25 297
20 293
27 265
29 236
34 206
30 133
21 121
2 101
38 92
31 87
35 76
36 73
26 72
32 70
37 61
33 61
39 40
Name: brand, dtype: int64
bodyType的特征分布如下:
bodyType特征有个8不同的值
7.0 12748
3.0 10808
4.0 9143
5.0 4175
6.0 3079
2.0 2484
1.0 1980
0.0 473
Name: bodyType, dtype: int64
fuelType的特征分布如下:
fuelType特征有个7不同的值
0.0 30045
5.0 14645
4.0 754
3.0 73
2.0 43
1.0 23
6.0 15
Name: fuelType, dtype: int64
gearbox的特征分布如下:
gearbox特征有个2不同的值
1.0 36935
0.0 10352
Name: gearbox, dtype: int64
notRepairedDamage的特征分布如下:
notRepairedDamage特征有个2不同的值
1.0 35555
0.0 4817
Name: notRepairedDamage, dtype: int64
regionCode的特征分布如下:
regionCode特征有个7078不同的值
487 122
868 93
539 46
32 46
222 46
...
3761 1
6232 1
7891 1
2106 1
2246 1
Name: regionCode, Length: 7078, dtype: int64
通过查看unique特征分布,可以对测试集与训练集数据分布情况进行比对
7.数字特征分析
相关性分析
查看几个特征得 偏度和峰值
每个数字特征得分布可视化
数字特征相互之间的关系可视化
多变量互相回归关系可视化
## 确定数据集中nan值的个数
Train_data1.isnull().sum()
SaleID 0
name 0
regDate 0
model 0
brand 0
bodyType 22605
fuelType 19858
gearbox 11584
power 0
kilometer 0
notRepairedDamage 44533
regionCode 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
v_15 0
v_16 0
v_17 0
v_18 0
v_19 0
v_20 0
v_21 0
v_22 0
v_23 0
dtype: int64
numeric_features = [col for col in numeric_features if col not in ['SaleID','name','bodyType','fuelType','gearbox','notRepairedDamage']]
numeric_features
['regDate',
'model',
'brand',
'power',
'kilometer',
'regionCode',
'creatDate',
'price',
'v_0',
'v_1',
'v_2',
'v_3',
'v_4',
'v_5',
'v_6',
'v_7',
'v_8',
'v_9',
'v_10',
'v_11',
'v_12',
'v_13',
'v_14',
'v_15',
'v_16',
'v_17',
'v_18',
'v_19',
'v_20',
'v_21',
'v_22',
'v_23']
## 1) 相关性分析
price_numeric = Train_data1[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'\n')
price 1.000000
v_0 0.521790
v_11 0.499157
v_15 0.414843
regDate 0.313313
power 0.193045
v_8 0.171495
v_10 0.153313
v_22 0.148351
v_7 0.148020
model 0.144848
v_12 0.116560
v_13 0.103143
v_14 0.064229
v_19 0.036949
v_20 0.030306
regionCode 0.016943
v_4 0.011313
creatDate -0.003412
v_2 -0.008591
brand -0.010469
v_23 -0.018257
v_5 -0.025231
v_6 -0.043621
v_21 -0.055471
v_17 -0.102734
v_9 -0.150717
v_1 -0.189762
v_16 -0.332209
kilometer -0.420236
v_18 -0.597190
v_3 -0.679661
Name: price, dtype: float64
f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True, vmax=0.8)

del price_numeric['price']
## 2) 查看几个特征得 偏度和峰值
for col in numeric_features:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(Train_data[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())
)
regDate Skewness: -1.54 Kurtosis: 011.04
model Skewness: 01.50 Kurtosis: 001.74
brand Skewness: 01.31 Kurtosis: 001.81
power Skewness: 58.59 Kurtosis: 4473.89
kilometer Skewness: -1.56 Kurtosis: 001.25
regionCode Skewness: 00.69 Kurtosis: -00.35
creatDate Skewness: -95.43 Kurtosis: 11376.69
price Skewness: 03.54 Kurtosis: 021.23
v_0 Skewness: -1.50 Kurtosis: 002.90
v_1 Skewness: 01.58 Kurtosis: 001.10
v_2 Skewness: 01.20 Kurtosis: 003.75
v_3 Skewness: 01.35 Kurtosis: 004.29
v_4 Skewness: 00.22 Kurtosis: 006.95
v_5 Skewness: 02.05 Kurtosis: 006.49
v_6 Skewness: 00.09 Kurtosis: -00.56
v_7 Skewness: 00.82 Kurtosis: -00.73
v_8 Skewness: -1.53 Kurtosis: 000.37
v_9 Skewness: 01.53 Kurtosis: 000.38
v_10 Skewness: -2.58 Kurtosis: 004.80
v_11 Skewness: -0.91 Kurtosis: 001.55
v_12 Skewness: -2.84 Kurtosis: 006.14
v_13 Skewness: -3.87 Kurtosis: 013.20
v_14 Skewness: 00.49 Kurtosis: -01.60
v_15 Skewness: 01.31 Kurtosis: -00.03
v_16 Skewness: 01.66 Kurtosis: 002.24
v_17 Skewness: 00.23 Kurtosis: 002.57
v_18 Skewness: 00.81 Kurtosis: 002.97
v_19 Skewness: 00.10 Kurtosis: 006.92
v_20 Skewness: 02.00 Kurtosis: 006.85
v_21 Skewness: 00.18 Kurtosis: -00.76
v_22 Skewness: 00.82 Kurtosis: -00.74
v_23 Skewness: 01.36 Kurtosis: 000.14
## 3) 每个数字特征得分布可视化
f = pd.melt(Train_data1, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")

Train_data1.head()
| SaleID | name | regDate | model | brand | bodyType | fuelType | gearbox | power | kilometer | ... | v_14 | v_15 | v_16 | v_17 | v_18 | v_19 | v_20 | v_21 | v_22 | v_23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 134890 | 734 | 20160002 | 13.0 | 9 | NaN | 0.0 | 1.0 | 0 | 15.0 | ... | 0.092139 | 0.000000 | 18.763832 | -1.512063 | -1.008718 | -12.100623 | -0.947052 | 9.077297 | 0.581214 | 3.945923 |
| 1 | 306648 | 196973 | 20080307 | 72.0 | 9 | 7.0 | 5.0 | 1.0 | 173 | 15.0 | ... | 0.001070 | 0.122335 | -5.685612 | -0.489963 | -2.223693 | -0.226865 | -0.658246 | -3.949621 | 4.593618 | -1.145653 |
| 2 | 340675 | 25347 | 20020312 | 18.0 | 12 | 3.0 | 0.0 | 1.0 | 50 | 12.5 | ... | 0.064410 | 0.003345 | -3.295700 | 1.816499 | 3.554439 | -0.683675 | 0.971495 | 2.625318 | -0.851922 | -1.246135 |
| 3 | 57332 | 5382 | 20000611 | 38.0 | 8 | 7.0 | 0.0 | 1.0 | 54 | 15.0 | ... | 0.069231 | 0.000000 | -3.405521 | 1.497826 | 4.782636 | 0.039101 | 1.227646 | 3.040629 | -0.801854 | -1.251894 |
| 4 | 265235 | 173174 | 20030109 | 87.0 | 0 | 5.0 | 5.0 | 1.0 | 131 | 3.0 | ... | 0.000099 | 0.001655 | -4.475429 | 0.124138 | 1.364567 | -0.319848 | -1.131568 | -3.303424 | -1.998466 | -1.279368 |
5 rows × 38 columns
## 4) 数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data1[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()

## 5) 多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data1['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data1['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data1['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data1['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data1['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data1['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data1['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data1['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data1['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data1['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)

8.类型特征分析
unique分布
类别特征箱形图可视化
类别特征的小提琴图可视化
类别特征的柱形图可视化类别
特征的每个类别频数可视化(count_plot)
## 1) unique分布
for fea in categorical_features:
print(Train_data1[fea].nunique())
250
40
8
7
2
2
categorical_features
['model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage']
## 2) 类别特征箱形图可视化
# 因为 name和 regionCode的类别太稀疏了,这里我们把不稀疏的几类画一下
categorical_features = ['model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage']
for c in categorical_features:
Train_data1[c] = Train_data1[c].astype('category')
if Train_data1[c].isnull().any():
Train_data1[c] = Train_data1[c].cat.add_categories(['MISSING'])
Train_data1[c] = Train_data1[c].fillna('MISSING')
def boxplot(x, y, **kwargs):
sns.boxplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data1, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")

## 3) 类别特征的小提琴图可视化
catg_list = categorical_features
target = 'price'
for catg in catg_list :
sns.violinplot(x=catg, y=target, data=Train_data)
plt.show()






[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zHNJrHWh-1618539021565)(output_70_0.png)]
categorical_features = ['model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage']
## 4) 类别特征的柱形图可视化
def bar_plot(x, y, **kwargs):
sns.barplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(bar_plot, "value", "price")

## 5) 类别特征的每个类别频数可视化(count_plot)
def count_plot(x, **kwargs):
sns.countplot(x=x)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")

9.用pandas_profiling生成数据报告
用pandas_profiling生成一个较为全面的可视化和数据报告(较为简单、方便) 最终打开html文件即可
import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")
第一遍可惜崩溃了,所以单独写了个文件跑界面,html界面也卡顿,应该是数据太大的缘故,这个建议报告可以取一些变量分批生成报告,生成的报告在资源里
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








