一、近似算法的概念
1、为啥要研究近似算法?
\quad 目前大规模的NPC问题我们无法通过计算得到,因此我们需要通过损失一部分精度的做法来找到多项式的近似算法。
2、近似算法精度的评价
\quad 用近似算法得到的解与原问题的最优解比值不超过 ρ ρ ρ,则称该算法是 ρ − 近 似 算 法 ρ-近似算法 ρ−近似算法。难点在于在不知道最优解的情况下证明近似解与最优解的近似程度。
二、几个经典的近似问题
1、负载均衡问题
\quad 负载均衡问题:给出 m m m个机器, n n n个任务,设任务 j j j处理时长为 t j t_j tj。要求如下:
- 每个任务只能在一个机器上不间断的完成
- 每个机器不能同时处理多个任务
\quad
设
S
[
i
]
S[i]
S[i]表示给机器
i
i
i处理的任务集合,则机器
i
i
i的处理时长为
L
[
i
]
=
∑
j
∈
S
[
i
]
t
j
L[i]=\sum_{j\in S[i]}t_j
L[i]=∑j∈S[i]tj。负载均衡问题的目标就是 找到一种任务分配方案使得
m
i
n
(
m
a
x
(
L
[
i
]
)
)
min(max(L[i]))
min(max(L[i])),即让每个机器处理的任务的时长尽可能均衡。
\quad
这个问题是NPC问题,因为
P
a
r
t
i
t
o
n
问
题
≤
P
负
载
均
衡
问
题
Partiton问题 \le_P 负载均衡问题
Partiton问题≤P负载均衡问题。
近似策略1
\quad 贪心策略:每次在机器中选出当前处理时长最短的机器处理下一个任务。时间复杂度为 O ( n l o g m ) O(nlogm) O(nlogm),对于每个任务都需要从 m m m个机器中选出处理时长最短的机器,这个用优先队列维护即可。这个近似算法是2-近似的,证明如下:
- 引理1:设最优解为 L ∗ L^* L∗,则 L ∗ ≥ m a x j t j L^*\geq max_jt_j L∗≥maxjtj,因为至少一个机器要处理一个任务,所有任务中花费时间最长的任务所需时间为 m a x j t j max_jt_j maxjtj,故得到此不等式。
- 引理2: L ∗ ≥ 1 m ∑ j t j L^* \geq \frac{1}{m}\sum_jt_j L∗≥m1∑jtj。当每个机器处理任务的时长相同时 L ∗ = 1 m ∑ j t j L^* = \frac{1}{m}\sum_jt_j L∗=m1∑jtj,显然其他情况下 L ∗ > 1 m ∑ j t j L^* > \frac{1}{m}\sum_jt_j L∗>m1∑jtj。
- 假设最后一个任务 j j j给了机器 i i i,说明在此之前,机器 i i i的负载时长最小,即 L [ i ] − t j ≤ L [ k ] ( 对 任 意 k 满 足 1 ≤ k ≤ m ) L[i]-t_j\le L[k](对任意k满足1 \le k \le m) L[i]−tj≤L[k](对任意k满足1≤k≤m)。
- 因为对任意一个机器 k k k都满足 L [ i ] − t j ≤ L [ k ] L[i]-t_j\le L[k] L[i]−tj≤L[k],因此 m ( L [ i ] − t j ) ≤ ∑ k L [ k ] m(L[i]-t_j)\le \sum_kL[k] m(L[i]−tj)≤∑kL[k],即 L [ i ] − t j ≤ 1 m ∑ k L [ k ] = 1 m ∑ j t j ≤ L ∗ ( 引 理 2 ) L[i]-t_j\le \frac{1}{m}\sum_kL[k]=\frac{1}{m}\sum_j t_j \le L^*(引理2) L[i]−tj≤m1∑kL[k]=m1∑jtj≤L∗(引理2)
- 到这里,该近似算法求解的结果 L = L [ i ] = ( L [ i ] − t j ) + t j ≤ L ∗ + L ∗ = 2 L ∗ L=L[i]=(L[i]-t_j)+t_j \le L^*+L^*=2L^* L=L[i]=(L[i]−tj)+tj≤L∗+L∗=2L∗,即 L ≤ 2 L ∗ L\le 2L^* L≤2L∗,该贪心策略是该问题的2-近似算法。
\quad 该近似算法能达到最优解的2倍吗,即上述不等式是紧的吗?是紧的!
近似策略2
\quad 策略2:将任务按照处理时长 t j t_j tj从大到小排序,之后再每次在机器中选出当前处理时长最短的机器处理下一个任务。时间复杂度为 O ( n l o g n + n l o g m ) O(nlogn+nlogm) O(nlogn+nlogm)。这个近似算法是 3 2 − 近 似 \frac{3}{2}-近似 23−近似的,证明如下:
- 引理3:假设有 m m m个机器,超过 m m m个任务,这些任务按照处理时长排好序, t 1 ≥ t 2 ≥ ⋯ ≥ t m + 1 ≥ ⋯ t_1\ge t_2 \ge \cdots \ge t_{m+1} \ge \cdots t1≥t2≥⋯≥tm+1≥⋯,则显然某个机器上至少要处理两个任务,则最优解 L ∗ ≥ 2 t m + 1 L^*\ge 2t_{m+1} L∗≥2tm+1。
- 从近似策略1的推导可以得到 L = L [ i ] = ( L [ i ] − t j ) + t j L=L[i]=(L[i]-t_j)+t_j L=L[i]=(L[i]−tj)+tj,假设机器 i i i上至少有2个任务,则利用引理3可得 t j ≤ 1 2 L ∗ t_j\le \frac{1}{2}L^* tj≤21L∗,故 L ≤ 3 2 L ∗ L\le \frac{3}{2}L^* L≤23L∗,该策略是该问题的 3 2 − 近 似 \frac{3}{2}-近似 23−近似算法。
\quad 该近似算法能达到最优解的 3 2 \frac{3}{2} 23倍吗,即上述不等式是紧的吗?不是紧的!
2、中心点选择问题
\quad
问题描述:给出
n
n
n个点
s
1
,
⋯
,
s
n
s_1,\cdots,s_n
s1,⋯,sn,从中选出
k
k
k个点
C
C
C,设每个点到最近的中心点
C
C
C的距离为
d
i
d_i
di,问采取何种策略选出这
k
k
k个点使得
r
(
C
)
=
m
a
x
(
d
i
)
r(C)=max(d_i)
r(C)=max(di)最小。这个问题是NPH问题。
\quad
贪心策略:初始时随机选一个点作为中心点,之后的
k
−
1
k-1
k−1次,每次遍历除已选做中心点的其他点,找出与该点距离最近的某个中心点计算出距离
d
j
d_j
dj。最后在这些点中找出
m
a
x
j
d
j
max_j d_j
maxjdj对应的点作为下一个中心点。这个近似算法是2-近似的,证明如下:
- 设 C ∗ C^* C∗是最优解对应的中心点, C C C是用上述贪心算法选出的中心点,则 r ( C ) ≤ 2 r ( C ∗ ) r(C)\le 2r(C^*) r(C)≤2r(C∗)。
3、带权顶点覆盖问题
\quad 图的每个顶点都有权重,找一个图的顶点集合能覆盖所有的边,问如何选择顶点使得这些顶点的权重和最小。用竞价法去近似求解。
- 对于某个顶点 i i i,其权重为 w i w_i wi,与该顶点相连的边记为 p p p,给这些边赋值权重,使得 ∑ e = ( i , j ) p e ≤ w i \sum_{e=(i,j)}p_e \le w_i ∑e=(i,j)pe≤wi。
- 设 S S S为任意一个集合覆盖,则 ∑ e p e ≤ ∑ i ∈ S ∑ e = ( i , j ) p e ≤ ∑ i ∈ S w i = w ( S ) \sum_ep_e\le \sum_{i\in S}\sum_{e=(i,j)}p_e\le \sum_{i\in S}w_i=w(S) ∑epe≤∑i∈S∑e=(i,j)pe≤∑i∈Swi=w(S),故 ∑ e p e ≤ w ( S ) \sum_ep_e\le w(S) ∑epe≤w(S)。
- 算法流程:对于图中任意一条边
e
=
(
i
,
j
)
e=(i,j)
e=(i,j),令
p
e
=
0
p_e=0
pe=0,当
i
,
j
i,j
i,j顶点的
∑
e
=
(
i
,
j
)
p
e
<
w
i
,
∑
e
=
(
i
,
j
)
p
e
<
w
j
\sum_{e=(i,j)}p_e<w_i,\sum_{e=(i,j)}p_e<w_j
∑e=(i,j)pe<wi,∑e=(i,j)pe<wj时,增加
p
e
p_e
pe直到满足
∑
e
=
(
i
,
j
)
p
e
=
w
i
或
者
∑
e
=
(
i
,
j
)
p
e
=
w
j
\sum_{e=(i,j)}p_e=w_i或者\sum_{e=(i,j)}p_e=w_j
∑e=(i,j)pe=wi或者∑e=(i,j)pe=wj。这时候相等的那个顶点放入
S
S
S中。

- 竞价法是2-近似算法,证明如下:
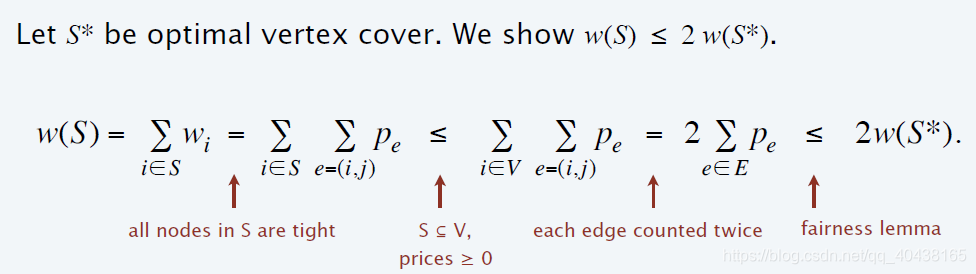
























 8208
8208

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








