FROM: https://blog.csdn.net/zhang0558/article/details/76019832
小波变换和小波阈值法去噪
1. 小波变换
小波变换是一种信号的时间——尺度(时间——频率)分析方法,它具有多分辨分析的特点,而且在时频两域都具有表征信号局部特征的能力,是一种窗口大小固定不变但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法。即在低频部分具有较低的时间分辨率和较高的频率分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于分析非平稳的信号和提取信号的局部特征,所以小波变换被誉为分析处理信号的显微镜。
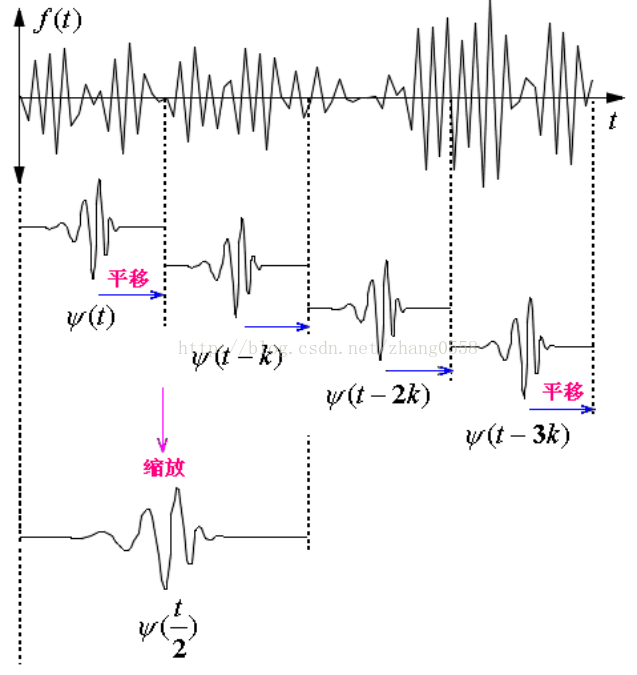
傅里叶是将信号分解成一系列不同频率的正余弦函数的叠加,同样小波变换是将信号分解为一系列的小波函数的叠加(或者说不同尺度、时间的小波函数拟合),而这些小波函数都是一个母小波经过平移和尺度伸缩得来的,如下图。
小波变换常见的形式有连续小波变换(CWT)、离散小波变换(DWT)等。连续小波变换是在尺度基础上连续变换的,做信号的小波分析得到的是幅值,a时间的三维图,对应的a值所截得的曲线即为该尺度的小波图形。而离散小波变换常用的是二进小波变换,对尺度和时间进行离散化处理。
CWT连续小波变换
CWT步骤:
首先选择一个小波基函数,固定一个尺度因子,将它与信号的初始段进行比较;
通过CWT的计算公式计算小波系数(反映了当前尺度下的小波与所对应的信号段的相似程度);
改变平移因子,使小波沿时间轴位移,重复上述两个步骤完成一次分析;
增加尺度因子,重复上述三个步骤进行第二次分析;
循环执行上述四个步骤,直到满足分析要求为止。
连续小波变换是在尺度基础上连续变换的,做信号的小波分析得到的是幅值,a时间的三维图,对应的a值所截得的曲线即为该尺度的小波图形。而集散小波变换常用的是二进小波变换。
但是,cwt的结果都相当于DWT中的细节信息(即所谓DWT中的高频信息。虽然越向后频率越低,有时已不能用“高频”来形容了,但这时的高频是相对概念,是相对于同阶逼近信息还是高的),只是其尺度是连续的尺度越大频率越低,一直低下去。
morlet等小波只能做CWT,有些是因为没法儿构造尺度函数,有些是根本就没有逆变换(只有满足某些条件,CWT才存在逆变换,这与小波基有关),有些是如何离散化也不能构成正交或双正交基,甚至按照二进制的离散化不能构成紧支的框架,所以它们通常不能做DWT,也就没有逆变换、重构一说了。
DWT离散小波变换
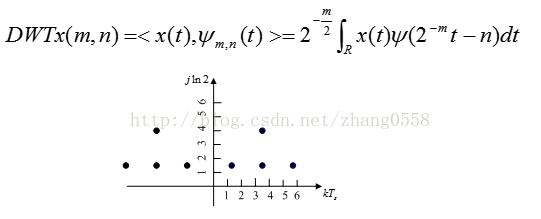
离散小波变换DWT对尺度参数按幂级数进行离散化处理,对时间进行均匀离散化取值如二进制离散化尺度时间为2,4,6,8...2n(要求采样率满足尼奎斯特采样定理),常用于信号的多分辨分析、信号分解重构。
多分辨分析也称为多尺度分析,是建立在函数空间概念上的理论。在不同的尺度和时间下,分别构造了尺度函数向量组合小波函数向量组,也即是尺度函数向量空间V与小波函数向量空间W,在一定层次下,信号在尺度空间做卷积所得到的是信号的近似、低频信息,信号在小波空间W做卷积所得到的是信号的细节、高频信息。(注意:尺度与分解层数不是一个概念,尺度与频率成反比的,分解层数是对频率的范围进行一定的划分)。
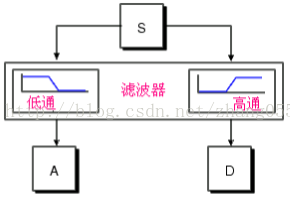
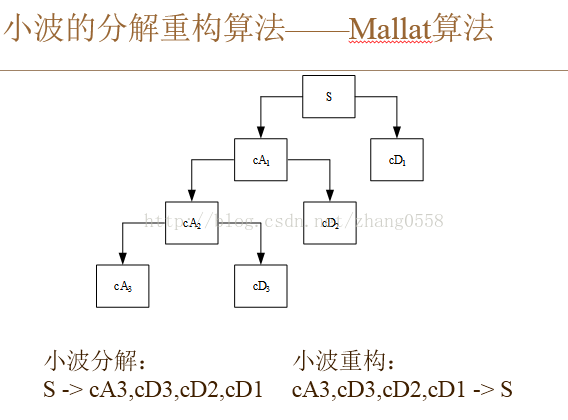
在多分辨分析中,如正交小波变换可以等效为一组镜像滤波的过程,即信号通过一个分解高通滤波器和分解低通滤波器,自然的高通滤波器输出对应的信号的高频分量部分,称为细节分量,低通滤波器输出对应了信号的相对较低的频率分量部分,称为近似分量。对应的快速算法称为Mallat算法。
小波分解重构过程(其中CA为低频信息、近似分量,CD为高频、细节分量):
小波阈值去噪
通常情况下, 我们在从设备上采集到的信号都是具有一定的噪声的,大多数情况下,可认为这种噪声为高斯白噪声。被噪声污染的信号=干净的信号+噪声。
为什么要使用阈值:由于信号在空间上(或者时间域)是有一定连续性的,因此在小波域,有效信号所产生的小波系数其模值往往较大;而高斯白噪声在空间上(或者时间域)是没有连续性的,因此噪声经过小波变换,在小波阈仍然表现为很强的随机性,通常仍认为是高斯白噪的。 那么就得到这样一个结论:在小波域,有效信号对应的系数很大,而噪声对应的系数很小。 刚刚已经说了,噪声在小波域对应的系数仍满足高斯白噪分布。如果在小波域,噪声的小波系数对应的方差为sigma,那么根据高斯分布的特性,绝大部分(99.99%)噪声系数都位于[-3*sigma,3*sigma]区间内(切比雪夫不等式, 3sigma准则)。因此,只要将区间[-3*sigma,3*sigma]内的系数置零(这就是常用的硬阈值函数的作用),就能最大程度抑制噪声的,同时只是稍微损伤有效信号。将经过阈值处理后的小波系数重构,就可以得到去噪后的信号。 常用的软阈值函数,是为了解决硬阈值函数“一刀切”导致的影响(模小于3*sigma的小波系数全部切除,大于3*sigma全部保留,势必会在小波域产生突变,导致去噪后结果产生局部的抖动,类似于傅立叶变换中频域的阶跃会在时域产生拖尾)。软阈值函数将模小于3*sigma的小波系数全部置零,而将模大于3*sigma的做一个比较特殊的处理,大于3*sigma的小波系数统一减去3*sigma,小于-3*sigma的小波系数统一加3*sigma。经过软阈值函数的作用,小波系数在小波域就比较光滑了,因此用软阈值去噪得到的图象看起来很平滑,类似于冬天通过窗户看外面一样,像有层雾罩在图像上似的。
比较硬阈值函数去噪和软阈值函数去噪:硬阈值函数去噪所得到的峰值信噪比(PSNR)较高,但是有局部抖动的现象;软阈值函数去噪所得到的PSNR不如硬阈值函数去噪,但是结果看起来很平滑,原因就是软阈值函数对小波系数进行了较大的 “社会主义改造”,小波系数改变很大。因此各种各样的阈值函数就出现了,其目的我认为就是要使大的系数保留,小的系数被剔出,而且在小波域系数过渡要平滑。
如何估计小波域噪声方差sigma的估计,这个很简单:把信号做小波变换,在每一个子带利用robust estimator估计就可以(可能高频带和低频带的方差不同)。 robust estimator就是将子带内的小波系数模按大小排列,然后取最中间那个,然后把最中间这个除以0.6745就得到噪声在某个子带内的方差sigma。利用这个sigma,然后选种阈值函数,就可以去去噪了,在matlab有实现api可使用。
小波阈值去噪过程
在小波分析中经常用到近似和细节,近似表示信号的高尺度,即低频信息;细节表示信号的低尺度,即高频信息。对含有噪声的信号,噪声分量的主要能量集中在小波解的细节分量中。
在以上过程中,小波基和分解层数的选择,阈值的选取规则,和阈值函数的设计,都是影响最终去噪效果的关键因素。
1、小波基的选择
可参考 http://blog.csdn.net/jbb0523/article/details/42586749 博文,一般选取小波基函数要从支撑长度、消失矩、对称性、正则性以及相似性等进行综合考虑。由于小波基函数在处理信号时各有特点,且没有任何一种小波基函数可以对所有类型信号都取得最优的去噪效果。一般来讲,db小波系和sym小波系在语音去噪中是经常会被用到的两族小波基。
2、分解层数的选择
对于一个要采集的信号,根据奈奎斯采样定理,其采样频率>= 2*信号的最大频率。而其他噪声频率如高斯白噪声的信号是幅度分布服从高斯分布,功率谱密度服从均匀分布的,并且与有效信号进行混合叠加的。
在小波分解中,分解层数的选择也是非常重要的一步。取得越大,则噪声和信号表现的不同特性越明显,越有利于二者的分离。但另一方面,分解层数越大,重构到的信号失真也会越大,在一定程度上又会影响最终去噪的效果。因此在应用时要格外注意处理好两者之间的矛盾,选择一个合适的分解尺度。
通常小波分解的频段范围与采样频率有关。若N层分解,则各个频段大小为Fs/2/2^N 。例如:一个原始信号,经历的时间长度为2秒,采样了2000个点,那么做除法,可得出采样频率为1000hz,由采样定理(做除法)得该信号的最大频率为500hz,那么对该信号做3层的DWT,一阶细节的频段为250-500hz,一阶逼近的频段为小于250hz,二阶细节的频段为125-250hz,逼近的频段为小于125hz,三阶细节的频段约为62.5-125hz,逼近的频段为小于62.5hz。对于更多阶的分解也是以此类推的。
3、阈值的选取
在小波域,有效信号对应的系数很大,而噪声对应的系数很小。噪声在小波域对应的系数仍满足高斯白噪分布。
阈值选择规则基于模型 y = f(t) + e,e是高斯白噪声N(0,1)。因此可以通过小波系数、或者原始信号来进行评估能够消除噪声在小波域的阈值。
目前常见的阈值选择方法有:固定阈值估计、极值阈值估计、无偏似然估计以及启发式估计等(N为信号长度)。
一般来讲,极值阈值估计和无偏似然估计方法比较保守,当噪声在信号的高频段分布较少时,这两种阈值估计方法效果较好可以将微弱的信号提取出来。而固定阈值估计和启发式阈值估计去噪比较彻底,在去噪时显得更为有效,但是也容易把有用的信号误认为噪声去掉。
4、 阈值函数选择
确定了高斯白噪声在小波系数(域)的阈值门限之后,就需要有个阈值函数对这个含有噪声系数的小波系数进行过滤,去除高斯噪声系数,常用的阈值函数有软阈值和硬阈值方法,很多文献论文中也有在阈值函数进行一些大量的改进和优化。
软硬阈值函数优缺点对比:
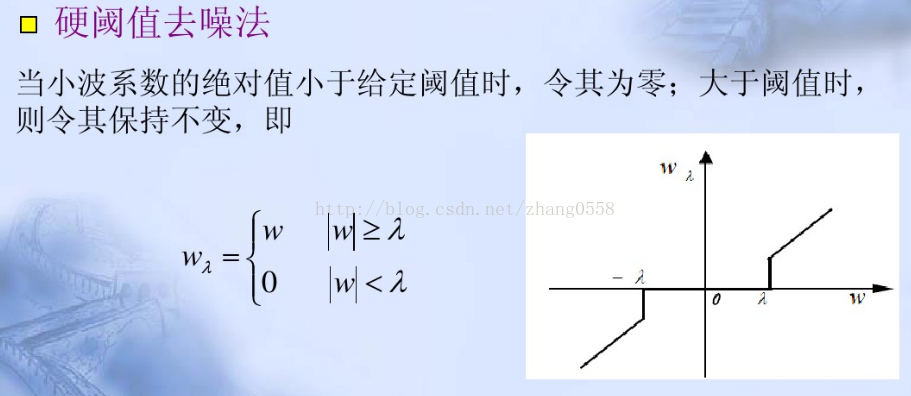
硬阈值函数在均方误差意义上优于软阈值法,但是信号会产生附加震荡,产生跳跃点,不具有原始信号的平滑性。
软阈值估计得到的小波系数整体连续性较好,从而使估计信号不会产生附加震荡,但是优于会压缩信号,会产生一定的偏差,直接影响到重构的信号与真实信号的逼近程度。
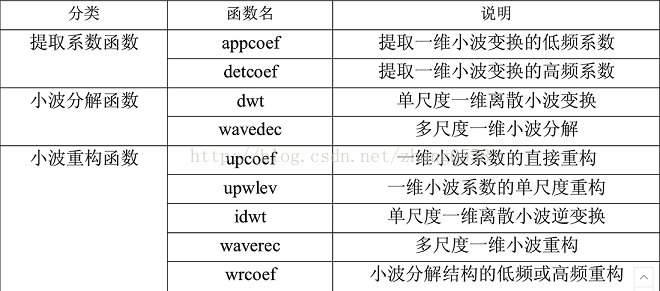
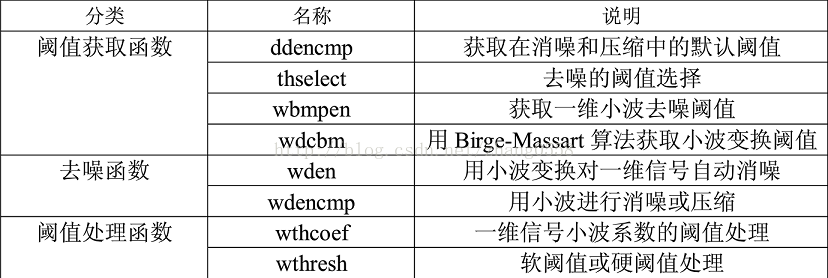
5、 matlab中小波工具箱
项目推荐:
Java微服务实战296集大型视频-谷粒商城【附代码和课件】
Java开发微服务畅购商城实战【全357集大项目】-附代码和课件











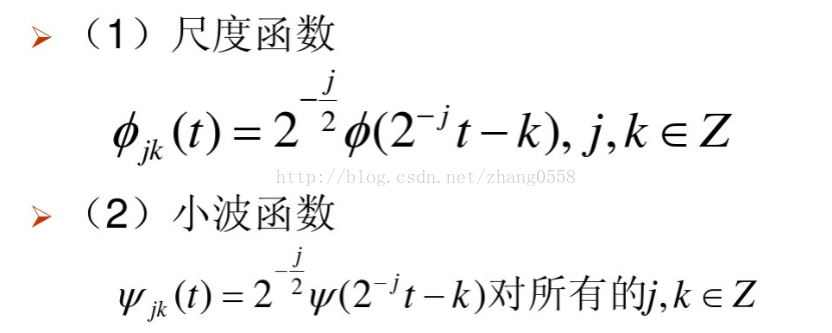




















 1200
1200











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








