本文详细介绍了小波阈值去噪算法，包括小波分解的理论、连续小波变换过程、去噪原理，以及阈值选择和改进方法。通过小波分解区分信号和噪声，然后利用阈值处理去除噪声，最后重构得到去噪信号。
小波阈值去噪
1.小波阈值去噪算法理论
通常我们采集的都不是纯净的音频，音频数据可以看做真实声音信号和噪声叠加而成。
含噪声信号的表达式为: s(t)=y(t)+n(t)
式中：y(t)为真实信号，n(t)为噪声信号，s(t)为含噪声信号。
小波阈值去噪的基本思想：通过分解+有选择地重构，实现去除噪声成分，留下关键信息。
我们可以从两个角度去理解小波阈值去噪，"小波"和“阈值”。
1.1小波
这里的小波指“小波分解”，而非小波变换、离散小波变换或者小波包分解等其它概念。小波（Wavelet），即小区域的波，是一种特殊的长度有限、均值为0的波形，它的能量是有限的，而且集中在某一点附近。其具有“小”和“波动性”两个特点。“小”：即时域具有紧支集或近似紧支集；“波动性”：正负交替，直流分量为0。小波分解基于信号的局部性质，将信号分解为不同频率和时间分辨率的小波系数。
FT将信号分解成一系列不同频率的正弦波（sin）叠加；小波变换则将信号分解成一系列小波函数(basic wavelet)的叠加（图，这些小波由一个母小波函数经尺度变换和平移得到。STFT是给信号加窗，分段做FFT，小波变换将STFT使用的无限长三角函数基换成了有限长会衰减的小波基，可以获取到频率和时间上的信息。
至于为什么要用小波变换，请参考如何通俗地讲解傅立叶分析和小波分析间的关系？
小波变换既有STFT的局部化思想，又克服了窗口大小不随频率变化、缺乏离散正交基的缺点。用不规则的小波函数来逼近尖锐变化的信号、以及逼近信号的局部特性比光滑的正弦函数好。
1.2CWT连续小波变换
连续小波变换是一种基于缩放和平移的小波分解方法。在连续小波变换中，信号与小波函数进行内积计算，得到一系列连续尺度和平移位置上的小波系数。连续小波变换具有连续性，可以提供更丰富的时频信息。
C
(
s
c
a
l
e
,
p
o
s
i
t
i
o
n
)
=
∫
−
∞
∞
f
(
t
)
ψ
(
s
c
a
l
e
,
p
o
s
i
t
i
o
n
,
t
)
d
t
C (scale, position)= \int_{-\infty} ^ \infty f(t) \psi(scale, position,t)dt
C(scale,position)=∫−∞∞f(t)ψ(scale,position,t)dt
上式表示小波变换是信号f（x）与被缩放和平移的小波函数ψ（）之积在信号存在的整个期间里求和的结果。变换结果是许多小波系数C，这些系数是关于缩放因子（scale）和平移（position）的函数。缩放因子越小，小波越窄。
小波阈值去噪的理论基础就是：
小波变换具有很强的去数据相关性，他能使信号的能量在小波域集中在一些大的小波系数当中，而噪声的能量却分布于整个小波域内。因此，经小波分解后，信号的小波系数幅值要大于噪声的系数幅值，可以认为，幅值比较大的小波系数一般以信号为主，而幅值比较小的系数在很大程度上是噪声。于是，采用阈值的办法，使大部分噪声系数减小至0，即将小于阈值部分的系数作为干扰噪声去除，然后再进行小波重构，从而实现降噪。【1】
1.3连续小波变换的步骤
（1）选择一个小波函数及变换尺度
（2）从信号起始位置开始，将小波函数与信号进行比较，计算系数小波系数C,C表示小波与该部分函数的相似程度
（3）沿时间轴移动小波函数，在新的位置计算小波系数，直至信号终点
（4）改变变换尺度，在所有尺度下重复上述步骤
1.4DWT离散小波变换
离散小波变换是一种基于滤波和下采样的小波分解方法。在离散小波变换中，信号经过一系列低通和高通滤波器后，被分为近似系数（低频成分）和细节系数（高频成分）。然后，这些系数被进一步分解为更低频和高频成分，直到达到所需的分解层数。
在连续小波变换中，scale、position、t是连续的，可以有无数多的取值，计算机无法在有限时间内完成计算任务，所以将他们离散化处理，得到离散小波变换。用s表示scale，T表示position
小波基函数：
ψ
(
s
,
T
,
t
)
=
1
s
ψ
(
t
−
T
s
)
\psi(s,T,t)= \frac{1}{\sqrt{\text{s}}} \psi( \frac{t - \text{T}}{\text{s}})
ψ(s,T,t)=s1ψ(st−T)
将小波基函数的scale和position限定在一些离散的点上取值
（1）尺度离散化
通常将尺度进行幂级数离散化，取s=sj0
初始值大于0，通常取2，j为0，1，2…
（2）位移离散化
T=k x sj0 x T0
对T取离散值，以覆盖整个时间轴，T满足奈奎斯特采样定理，在 尺度s=2j时，沿时间轴的采样间隔是2j*T0。
由于信号可以通过一组不同位置和尺度的小波基函数进行分解，则频率可以定义为f=1/Δt,Δt是时间间隔，与尺度s相关，即Δt=s,所以f=1/s。j每增加1，尺度增加一倍，则对应的频率减小一半，此时采样率可降低一半而不至于引起信息丢失。
2.小波去噪原理
信号经过小波变换得到的小波系数含有重要的时频信息，真实信号的小波系数较大，噪声的小波系数较小，选取一个合适的阈值，保留系数较大的，将小的置0，就可保留信号滤除噪声。
2.1小波去噪的基本步骤：
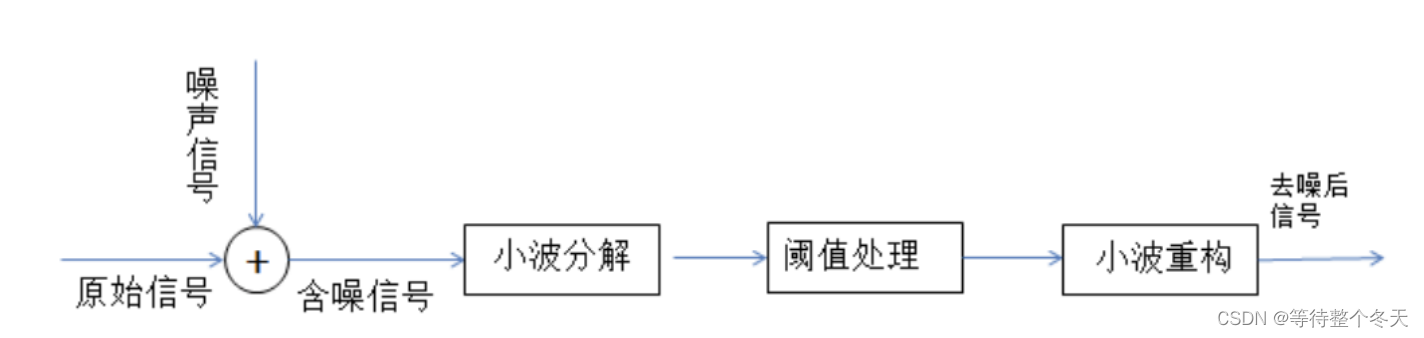
含噪声信号的表达式为: s(t)=y(t)+n(t)
-
信号的小波分解
选择一个小波基类型与小波分解的层次N，对含噪信号进行N层小波分解，得到各层的小波系数
-
小波分解高频系数的阈值量化
对第一层到第N层的高频小波系数采取合适的阈值进行量化，利用其去相关性去除噪声。量化处理方法主要有硬阈值量化（左）和软阈值量化（右）。硬阈值方法可以很好地保留信号边缘等局部特征，软阈值处理相对要平滑，但会造成边缘模糊等失真现象
-
信号的小波重构
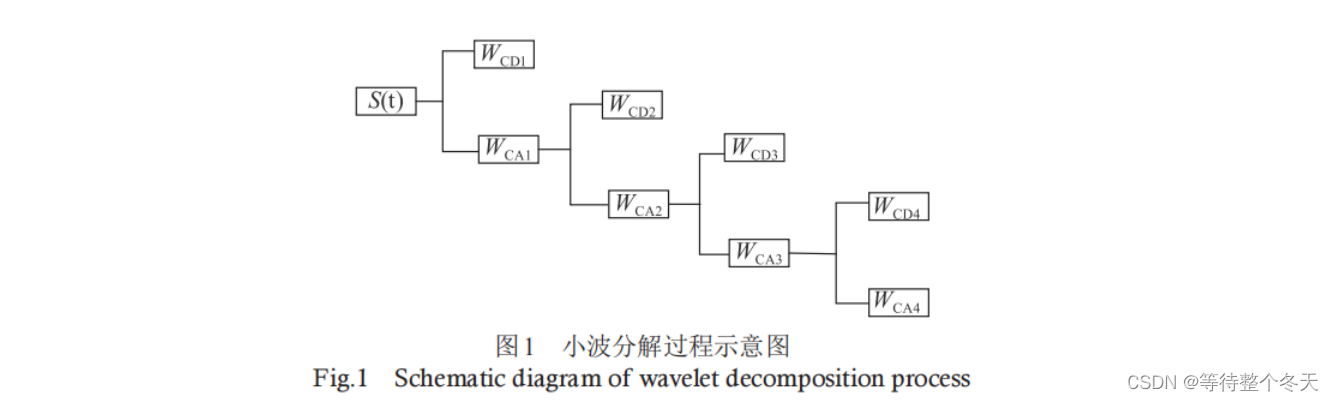
对处理后的信号重构，得到去噪声后的信号。如下图对信号s(t)进行4层小波分解，其中
WCD1~WCD4 为每层小波分解的高频小波系数，WCA1~WCA4为低频小波系数，噪声主要包含在低频小波系数中，所以需要采用一个合适的阈值来抑制低频小波系数，
2.2 阈值的选择
-
软阈值滤波
软阈值通常设置一个阈值λ，当小波系数向0收敛过程中，大于λ的系数，置为sgn（W）(|W|-λ)，对于小于λ的小波系数，直接置0，可以获得更加平滑的去噪信号。
-
硬阈值滤波
硬阈值不同之处在于小波系数大于λ时，保留其原值，可以较好保留其原始特征
2.2改进型小波阈值去噪
噪声的小波系数随着分解尺度增大而减小，固定阈值存在过扼杀现象
软阈值法函数小波系数的绝对值总小于实际值，会导致在信号重构的时候产生误差。硬阈值法，阈值点出估计的小波系数不连续，信号重构过程中，阈值点处会产生震荡与振铃现象，传统的软硬阈值法会造成过度去噪。
网上有很多改进方法，大家可以自行查阅。
【滤波专题-第6篇】小波阈值去噪方法看这一篇就明白了~（附MATLAB实现）
参考资料：
[1]王异凡, 朱冠霖, 王兆强,等. 基于改进小波阈值的GIS局部放电在线监测白噪声干扰抑制研究[J]. 高压电器, 2019(3):8
扫一扫
4万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
