样本T检验

单样本T检验
- 用到一个连续变量
独立样本T检验

- 用到一个连续变量 + 一个分类变量(也可以将连续变量进行分组得到一个分类变量)
- 方差齐性及检验:
- 原假设:两组配对数据之间没有显著差异
- 研究假设:两组配对数据之间有显著差异
- 当P<0.05,则研究假设成立,即两组中总体的方差是不等的,需要看第二行的t值检验结果,反之则看第一行的t值结果
- 解读:
- 方差方程的Levene检验(就是方差齐性检验):sig=0.04<0.05,因此,两组中总体方差不一致,看第二行数据;
- Sig(双侧)小于0.05,说明检验中的研究假设成立,退休前后的收入均值有差异;
- 组统计量:差异为多少呢?参照组统计量中的均值即可;

配对样本T检验
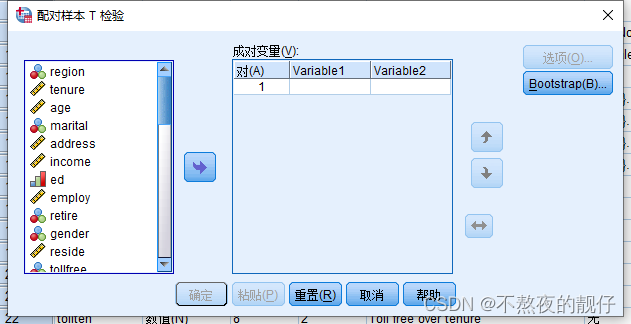
- 用到一个总体中的两个样本

非参数检验

单因素检验

- 如何选择方差齐性检验
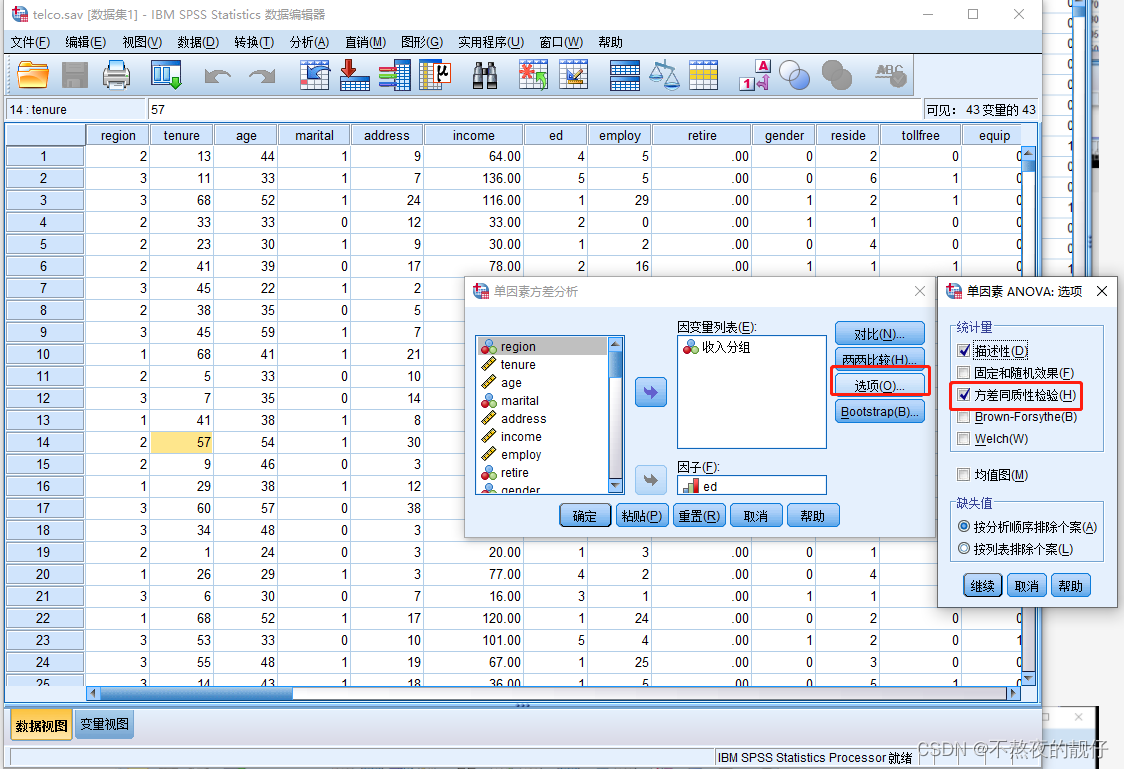
- 假定方差齐性:如果方差相等,则选择这类方式
- 未假定方差齐性:如果方差不相等,则选择这类方式

- 具有显著性差异的因素都标了星号“*”

多因素检验
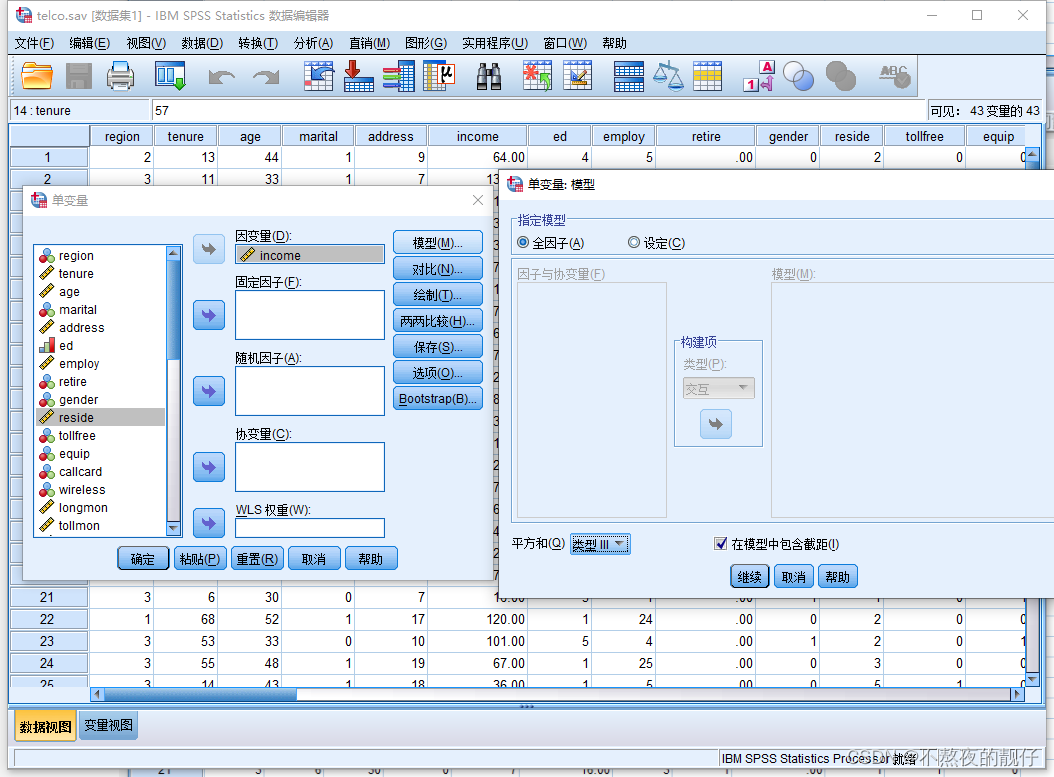
- 单变量:指单个因变量


- 模型
- 全因子:即考虑所有自变量对于因变量的直接效应,又考虑所有分类变量的交互作用对因变量的影响
- 设定(定制模型):可根据研究者自身需求,定制需要考虑的对因变量的影响因素。比如:只考虑自变量的直接效应,或部分自变量的交互作用。
- 当自变量特别多是,尤其是分类自变量特别多时,且样本量不多时,应该使用定制模型。
- WHY:
- 分类变量特别多:容易造成分类之后的样本不属于在总体中具有代表性的样本数据;
- 样本量不多:分类变量特别多,容易造成分类之后某个单元之中的缺少元素;
- 每个分类下的样本量
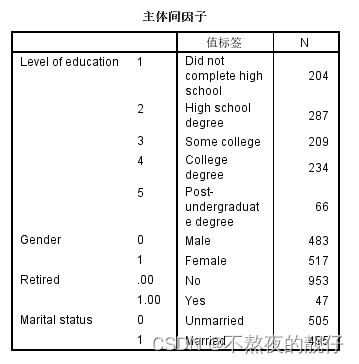
- 字段含义
- Ⅲ型平方和:离差平方和
- df:自由度
- 均方:Ⅲ型平方和 ÷ 自由度
- F:某行均方 ÷ 误差行均方
- sig:根据F函数计算得出,F越大,P值越小
- R方:
- 如何判断自变量对因变量有影响:
- 观察自变量对应的显著性水平:若小于0.05,研究假设成立(自变量对因变量有显著性影响)

- 观察自变量对应的显著性水平:若小于0.05,研究假设成立(自变量对因变量有显著性影响)
相关分析
双变量相关


偏相关

回归分析
线性回归
分类变量的虚拟变量的转换


- 需要将原始值和原始值以外的其他值转换成对应的值,用于比较的变量全部变为0

回归分析




回归分析的结果解读
将自变量全部输入
- 拟合优度检验
- R²值和方差检验F值
- R²值:自变量对因变量的解读能力。
- F值:F值对应的概率P值<0.05,研究假设成立,即至少有一个自变量对因变量存在显著影响。
- Durbin-Watson值:残差检验:DW值越接近2,表示残差越不存在自相关性。

- 参数显著性检验
- t值:根据每个自变量的t值对应的概率P值,是否<0.05,如<0.05,则研究假设成立,即该自变量对因变量存在显著影响。
- 则下述图表的结果解读为:ed1、ed2、ed3、ed4、employer对因变量显著影响,其余没有;
- 标准化系数:通过标准化系数,判断两者对因变量的影响程度大小
- 则下述图表的结果解读为:明显employer相比与ed1、ed2、ed3、ed4来说对因变量影响更大;
- B值:在其他变量不变的情况下,因变量受自变量影响的大小
- 则下述图表的结果解读为(如何解读employer):employer(自变量)每增加一个单位,则income(因变量)平均增加6.279个单位。
- 则下述图表的结果解读为(如何解读ed1、ed2、ed3、ed4):ed1=-51.042表示ed1代表的学历(高中以下)比对照的学历人群(大专,原分类中的数值3)在因变量家庭收入上,平均低51.042个单位。
- 共线性统计量:
- 容差:
- VIF:通常根据VIF值,当VIF>10,自变量之间存在共线性,若存在共线性,则需要更换变量选择的方式(进入变更为逐步or其他,消除共线性)。



- t值:根据每个自变量的t值对应的概率P值,是否<0.05,如<0.05,则研究假设成立,即该自变量对因变量存在显著影响。
- 残差

- 点越集中在斜线上,说明数据越服从正态分布。

将自变量“逐步”输入(逐步回归法)
- 将对因变量没有显著影响的自变量从模型中删除,得到干净的模型。
- 则下述图表的结果解读为:模型经历了三步建模,自变量逐步加入了模型中,同时R方值在不断提高。

- 回归方程:y = 34.601 + 6.021*[employer] - 62.647*[ed1] - 36.379*[ed2]
- 但可以看出来,这里学历缺失了一部分,这是不合理的,学历是一个整体,不能独立某一部分影响因变量。因此,采用层级分布!!!

- 但可以看出来,这里学历缺失了一部分,这是不合理的,学历是一个整体,不能独立某一部分影响因变量。因此,采用层级分布!!!
层级分布
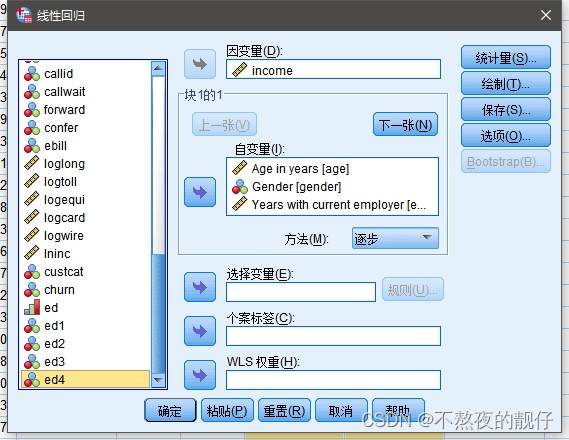

- 可以看到:ed1、ed2、ed3、ed4其实都是对因变量有影响的,那为什么逐步回归法没有加入ed3、ed4
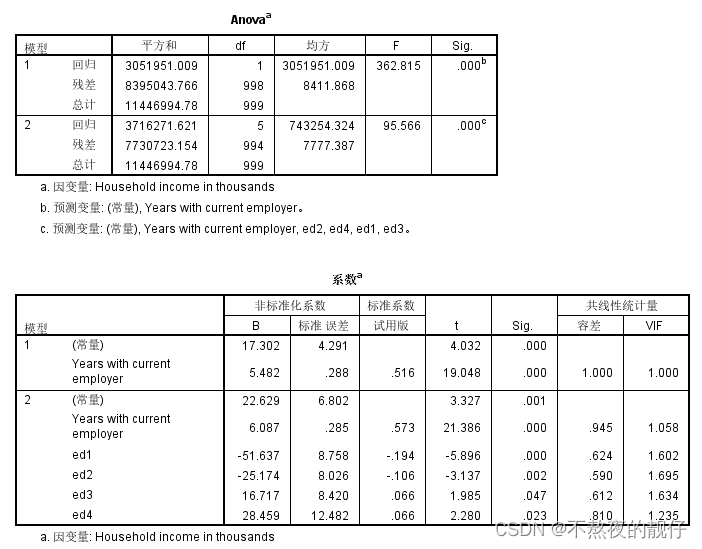
- 对比两个模型的调整后R方,可以看出ed3、ed4加入之后R方上升不大,因此可能是被软件建模过程中忽略舍去了。


- 因此,我们根据完整的ed1、ed2、ed3、ed4对回归方程进行书写,得到
- y = 22.629 + 6.087*[employer] - 51.637*[ed1] - 25.174*[ed2] + 16.717*[ed3] + 28.459*[ed4]

- y = 22.629 + 6.087*[employer] - 51.637*[ed1] - 25.174*[ed2] + 16.717*[ed3] + 28.459*[ed4]
非线性回归
- 操作:
- 先通过散点图判断是否存在非线性关系


- 先通过散点图判断是否存在非线性关系
- 可以看到:符合、增长、指数方程建立的模型都很优秀。

- 根据指数模型来构建方程,得到:
- income = e^Ininc

- income = e^Ininc
- 检验:方式一


- 返回数据集中进行数据验证

- 检验:方式二


因子分析

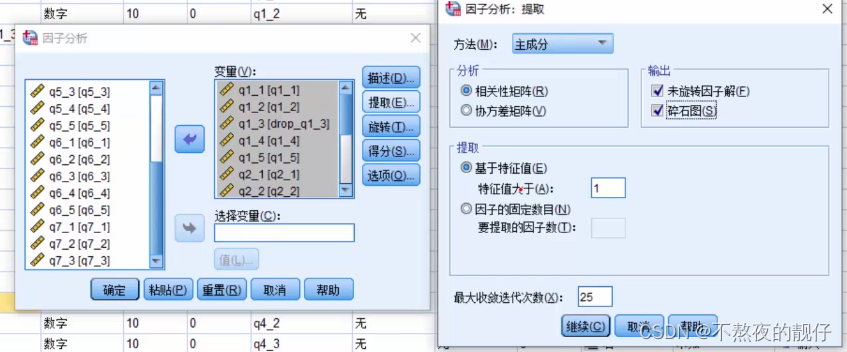


- 绝对值如下:排除绝对值小于输入值的数据,在成分矩阵中显示空白

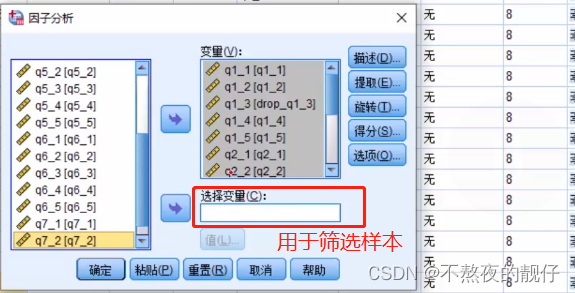
结果解读
- 结果解读1:KMO值>0.7,适合做因子分析。

- 每个变量提取的信息量

- 如何判断因子数量,根据因子的特征值判断,若>1则提取因子。
- 总计:特征值。
- 对提取的四个因子进行旋转。
- 累计%:如果通过因子分析降维后做综合评价, 那么累计方差贡献率需要大于80%。效度检验或其他分析,大于60%即可。

- 根据碎石图的拐点判断保留的因子数,但代表性不大

- 表格里面的值:因子载荷值
- 值>0.5,具有代表性
- 但由于目前的因子载荷值会出现代表两个因子的情况,因子代表情况不清晰,因此需要进行旋转。

- 旋转后的因子载荷值:
- 代表值清晰明了;
- 为什么会出现因子按照从大到小排序,同时会有空白值:
- 排序:因子分析-选项-系数显示格式:勾选了“按大小排序”;
- 空白值:因子分析-选项-系数显示格式:勾选了“排除小系数”;

- 结果解读2:因子的划分:根据变量在每个因子中的取值是否大于0.5;
- 根据成分矩阵,就可以对因子进行命名了。
- 效度检验:
- 第一个判断标准:每个变量有且只有一个因子载荷值大于0.5,若所有因子载荷值均小于0.5,说明该变量不具有收敛效度,需删除;
- 收敛效度:变量可以收敛到某个因子中去;
- 第二个判断标准:变量在两个或以上因子中的载荷值同时大于0.5,则说明该变量不具有区分效度,需删除;
- 第二个判断标准:某变量单独成为一个因子(即变量在所有因子中的载荷值均小于0.5),则说明该变量也不存在收敛效度。
- 第一个判断标准:每个变量有且只有一个因子载荷值大于0.5,若所有因子载荷值均小于0.5,说明该变量不具有收敛效度,需删除;
- 结果解读:因子得分计算
- 软件会根据自动生成因子得分,在数据视图的最后部分新增,但这部分数据都是经过了标准化(均值 = 0,方差 = 1);
- 若不想要标准化之后的因子得分,需要原始的因子得分:
- F1 = X1a1 + X2a2 + X3*a3 + …… + Xn * an
- F2 = X1b1 + X2b2 + X3*b3 + …… + Xn * bn
……

logistic回归
二元logistic回归
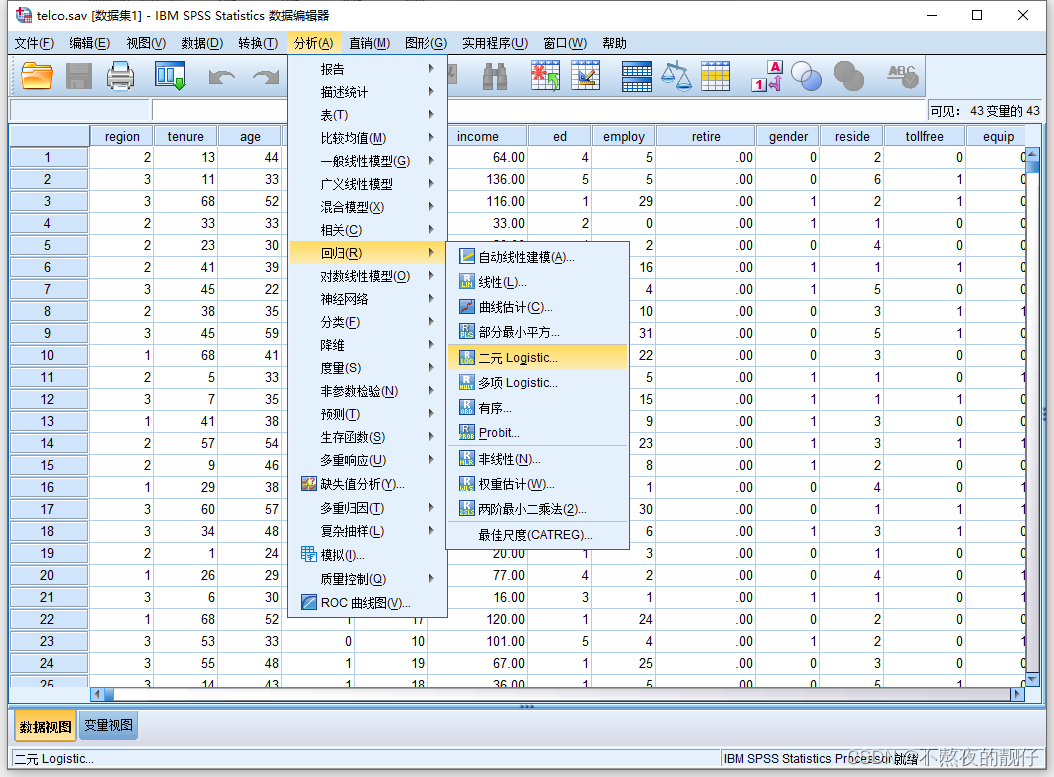
选项
- 分类:将分类变量转为虚拟变量

- 保存

- 选项:
- 分类标准值:超过这个值判断为真,一般为0.5
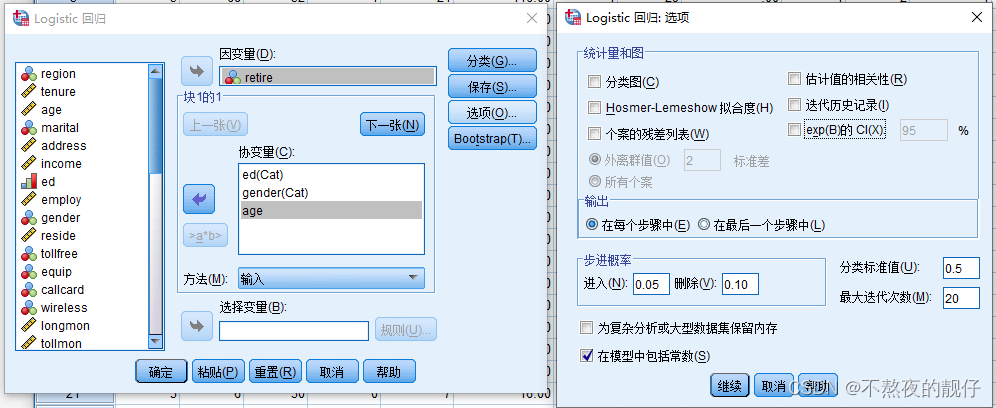

- 分类标准值:超过这个值判断为真,一般为0.5
结果解读

-
在模型中不放任何自变量,对模型进行预测,预测准确率为95.3%
- 已观测列:源数据中有953个No,47个Yes;
- 已预测列:预测中为No,源数据中为No的有953个;预测中为No,源数据中为Yes的有47个;

-
加入自变量之后

-
如何判断自变量对因变量有影响:
- 根据P值(Sig.)小于0.05,拒绝原假设,自变量对因变量存在显著影响;
- 根据Wals值:值越高,自变量对因变量的影响程度越大;
- Exp(B):对B列求以e为底的指数:优势比(OR值):
- 值>1,该自变量会增加自变量取1的概率发生;
- 值<1,该自变量会降低自变量取1的概率发生。
-
解读图表:
- 连续自变量对因变量的影响程度:在其它因素不变的情况下,随着age自变量每增加一个单位,优势比增加1.385倍(即退休的概率增大);
- 分类自变量对因变量的影响程度:在其它因素不变的情况下,ed(2)的优势比是原ed中研究生学历(参考值)优势比的0.120倍(大专学历高于研究生学历的退休概率);
-
logistic公式
l n ( P 1 − P ) = − 20.305 − 0.782 ∗ e d 1 − 0.561 ∗ e d 2 − 2.121 ∗ e d 3 ∗ 1.897 ∗ e d 4 − 0.429 ∗ g e n d e r + 0.326 ∗ a g e ln(\frac P {1-P})=-20.305-0.782*ed1-0.561*ed2-2.121*ed3*1.897*ed4-0.429*gender+0.326*age ln(1−PP)=−20.305−0.782∗ed1−0.561∗ed2−2.121∗ed3∗1.897∗ed4−0.429∗gender+0.326∗age

-
将gender、age根据wals向前加入到模型中,ed强制加入到模型中;
- 发现gender被去掉之后ed对模型不存在显著影响了,判断可能性别和学历之间对退休这个因变量有交互作用,考虑将两个交互变量加入模型中;

- 发现gender被去掉之后ed对模型不存在显著影响了,判断可能性别和学历之间对退休这个因变量有交互作用,考虑将两个交互变量加入模型中;
多元无序多分类
操作

- 选择对比项,即选择进行二分类的对比向

- 因子:分类变量
- 协变量:连续变量

- 含义:(具体详见多因素检验的解释)
- 主效应:只考虑自变量的直接效应,不考虑交互效应
- 全因子:即考虑直接效应,又考虑交互效应

-模型:判断模型好坏


结果解读
- 频次统计

- 拟合优度检验:显著水平p值>0.05
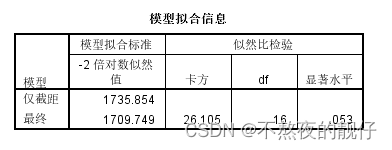
- 通常情况下不参考这个值

- 显著水平<0.05,拒绝原价设,表示学历与地区有一定的相关性。

- 可以看到你年龄、套餐对地区没有影响,学历仅对于地区二、地区三有一定相关性。

数据集变化
- 根据ESTn_1得到的概率,选择概率最高的对样本进行分类。

多元有序多分类
操作
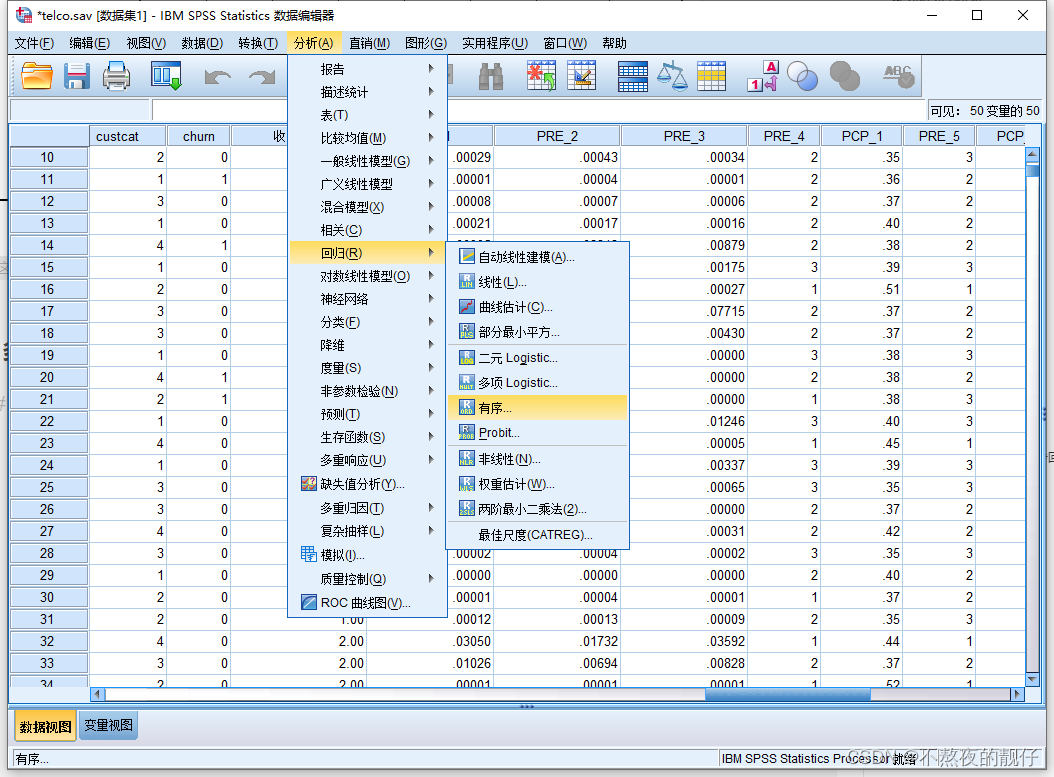


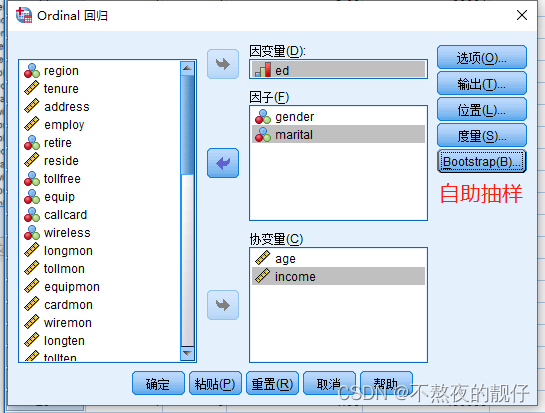
结果解读
- 若为0的频率大于60%,则模型结果参考意义不大

- 频次统计

- 自变量当中至少有一个对因变量有影响作用

- Pearson显著性>0.05,模型结果可参考。
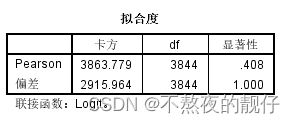
- 平行线检验:
- 显著性大于0.05,接受原假设,在因变量的不同切割建立的二元逻辑回归方程中,自变量对因变量的影响程度是相同的。
- 因此,可以建立有序多元logistic回归模型。

- 根据阈值可以看到模型切割了四次
- gender、marital两个变量的显著性均大于0.05,对因变量没有影响;
- 因此,模型中可以剔除。

- 平行线检验依旧成立
- 参数估计值
- 模型公式:
- 公式一: l n ( p 1 1 − p 1 ) = − 2.494 − 0.032 ∗ a g e + 0.003 ∗ i n c o m e ( p 1 代 表 学 历 取 1 的 概 率 ) ln(\frac {p1} {1-{p1}})=-2.494-0.032*age+0.003*income(p1代表学历取1的概率) ln(1−p1p1)=−2.494−0.032∗age+0.003∗income(p1代表学历取1的概率)
- 公式二: l n ( p 2 1 − p 2 ) = − 1.110 − 0.032 ∗ a g e + 0.003 ∗ i n c o m e ( p 2 代 表 学 历 取 1 和 2 的 概 率 ) ln(\frac {p2} {1-{p2}})=-1.110-0.032*age+0.003*income(p2代表学历取1和2的概率) ln(1−p2p2)=−1.110−0.032∗age+0.003∗income(p2代表学历取1和2的概率)
- 公式三: l n ( p 3 1 − p 3 ) = − 0.192 − 0.032 ∗ a g e + 0.003 ∗ i n c o m e ( p 3 代 表 学 历 取 1 、 2 、 3 的 概 率 ) ln(\frac {p3} {1-{p3}})=-0.192-0.032*age+0.003*income(p3代表学历取1、2、3的概率) ln(1−p3p3)=−0.192−0.032∗age+0.003∗income(p3代表学历取1、2、3的概率)
- 公式四: l n ( p 4 1 − p 4 ) = 1.649 − 0.032 ∗ a g e + 0.003 ∗ i n c o m e ( p 2 代 表 学 历 取 1 、 2 、 3 、 4 的 概 率 ) ln(\frac {p4} {1-{p4}})=1.649-0.032*age+0.003*income(p2代表学历取1、2、3、4的概率) ln(1−p4p4)=1.649−0.032∗age+0.003∗income(p2代表学历取1、2、3、4的概率)
- 公式解读:公式一:
- 年龄每增加一个单位,优势比增加-0.032倍(即年龄越大,取学历小的概率越小,则学历大的概率越大);
- 年龄每增加一个单位,优势比增加0.003倍(即收入越大,取学历小的概率越大,则学历大的概率越小)

- 模型公式:
数据集变化
-
- 根据ESTn_1得到的概率,选择概率最高的对样本进行分类。

- 根据ESTn_1得到的概率,选择概率最高的对样本进行分类。
时间序列
操作
- 要做时间序列需要定义软件认可的格式才可以
- 定义时间格式:
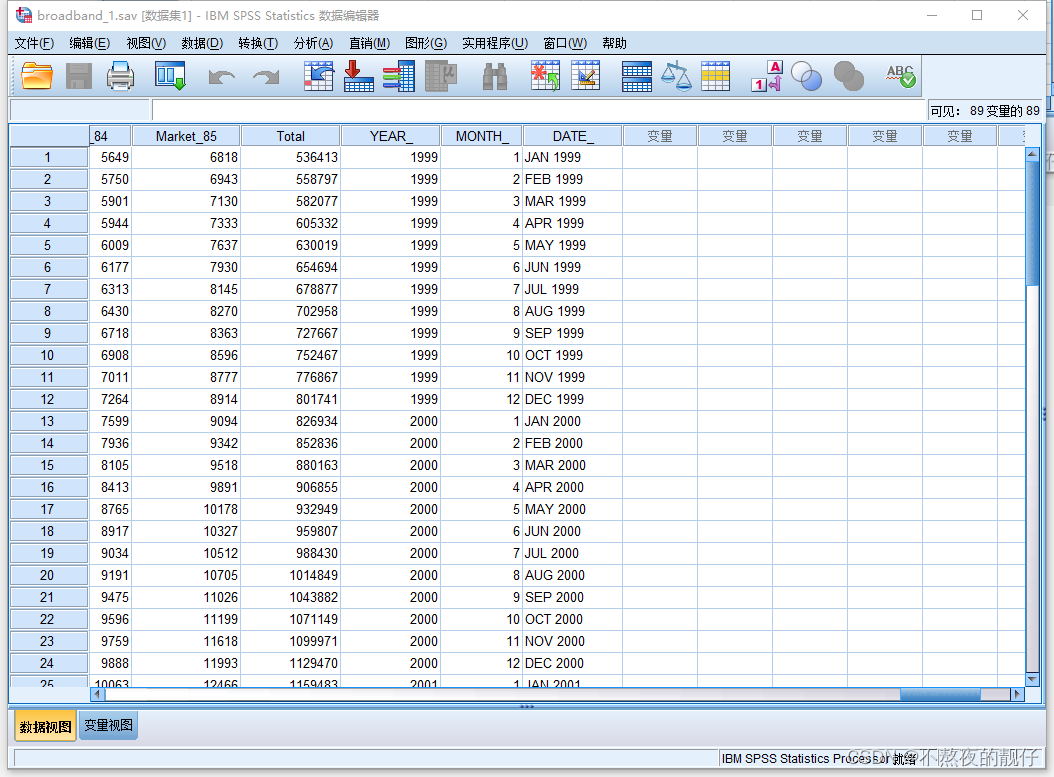

频谱分析
- 做语音分析的时候用
- 判断数据当中的周期性

普通ARIMA模型建模
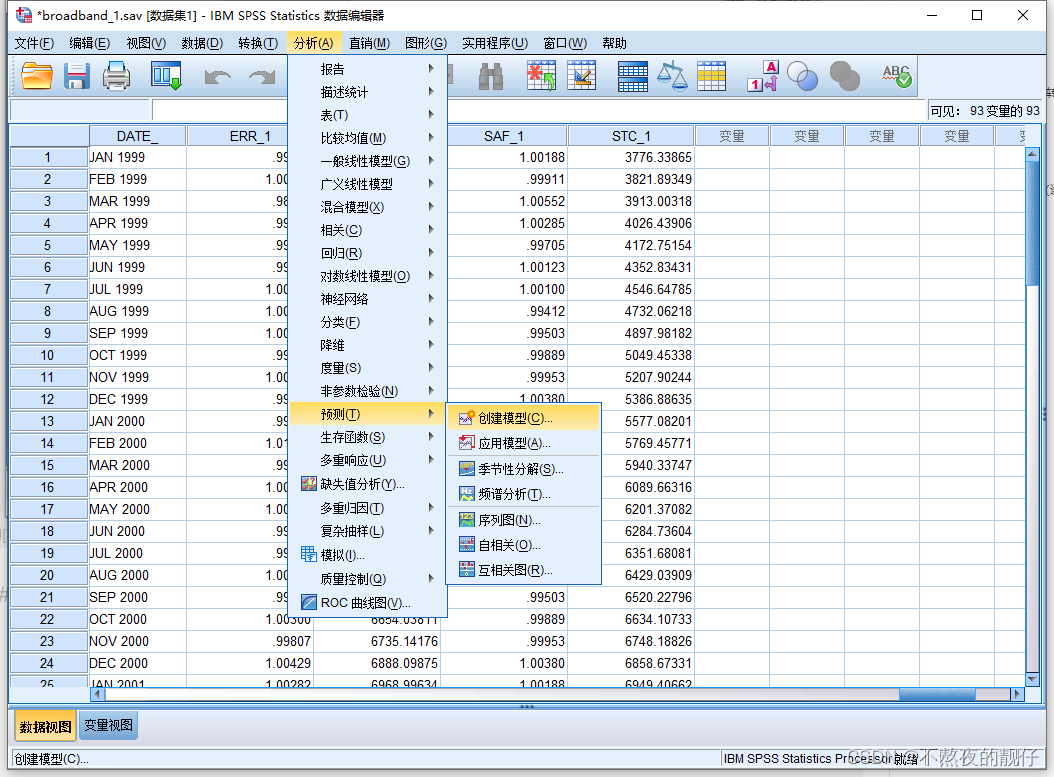
- 若添加了自变量,指的是自变量和因变量有相关关系,不考虑自变量的滞后性


- 统计量:通过各种数值判断模型好坏

- 绘图

- 保存:将预测值保存到数据当中
- 通常只保存预测值

- 通常只保存预测值
- 选项
- 模型评估期后的第一个个案到活动数据集内的最后一个个案:当前数据集中有需要预测的日期;
- 模型评估期后的第一个个案到指定日期之间的个案:当前数据集中没有需要预测的日期,需要输入数据。

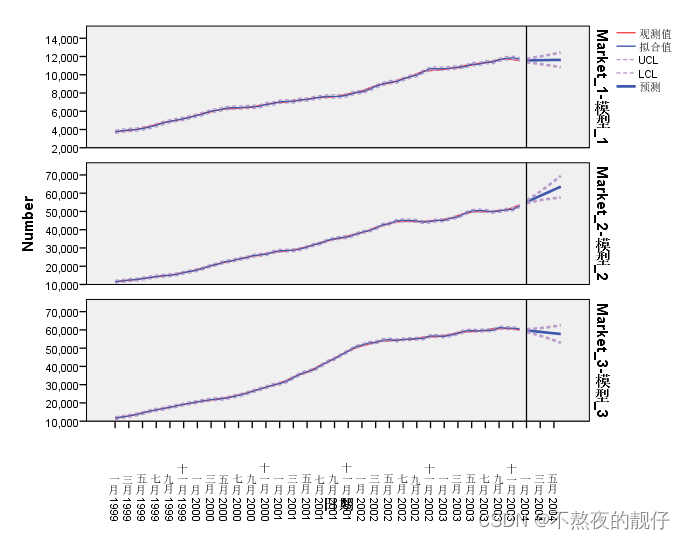
专家建模器结果解读(模型类型:所有)
- 建立了三个Holt模型:Holt模型适用于具有趋势性,但没有明显周期性的数据

- 数据解读
- Ljung-Box Q:
- 原假设:模型可以很好的拟合数据。即概率值Sig.(P值)越大,模型越好。
- Market 1、Market 3的模型是可以接受的

- Ljung-Box Q:
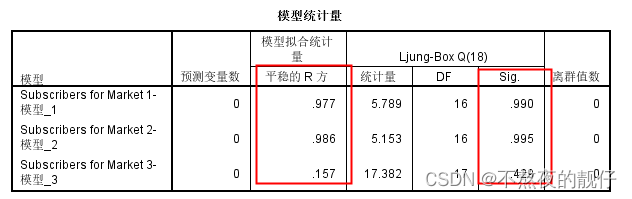
专家建模器结果解读(模型类型:仅限ARIMA模型)

-
ARIMA(1,0,0)(1,0,0):解释:第一个括号内(p,d,q),第二个括号内(季节性因素)
- 模型使用了过去1个月,过去12个月来预测当前月的数值
- 模型没有使用差分,以及移动平均

-
Market 1、Market 2的R²增大,置信度增大
-
Market 3的R²减小,置信度降低
-
M a r k e t 1 : Y t = 8.579 + 0.999 ∗ Y t − 1 + 0.633 ∗ Y t − 12 Market 1:Y_t = 8.579 + 0.999*Y_{t-1} + 0.633*Y_{t-12} Market1:Yt=8.579+0.999∗Yt−1+0.633∗Yt−12

-
模型预测的越不好,置信区间就会越大;反之,越小。

因果ARIMA模型建模
操作
- 目标:因变量;最好选择数值型的连续变量
- 输入:自变量;
- 候选输入:自变量候选项;
- 强制输入:自变量必选项,一定要考虑的和加入模型的变量;
- 目标和输入:既是自变量,又是因变量;

- 预测Market 1的销售额
- 认为Market 2、Market4对Market 1的销售额都有影响

- 认为Market 2、Market4对Market 1的销售额都有影响
- 最好不要有缺失值
- 缺失值处理在SPSS自带的操作中也有

- 方法:线性插值和线性趋势预测的缺失值往往是一样的。
- 线性插值:利用时间序列建立线性直线,预测缺失值
- 临近点平均值:利用前面两个点+后面两个点(共计四个点)的均值来代替缺失值
- 临近点中间值:利用前面两个点+后面两个点(共计四个点)的中位值来代替缺失值
- 线性趋势:利用时间序列建立线性回归,预测缺失值

- 缺失值处理在SPSS自带的操作中也有
- 要显示的序列
- 固定目标数:如果因变量特别多,可以限制因变量的个数
- 输出选项:


- 指定从什么时间预测到什么时间

结果解读
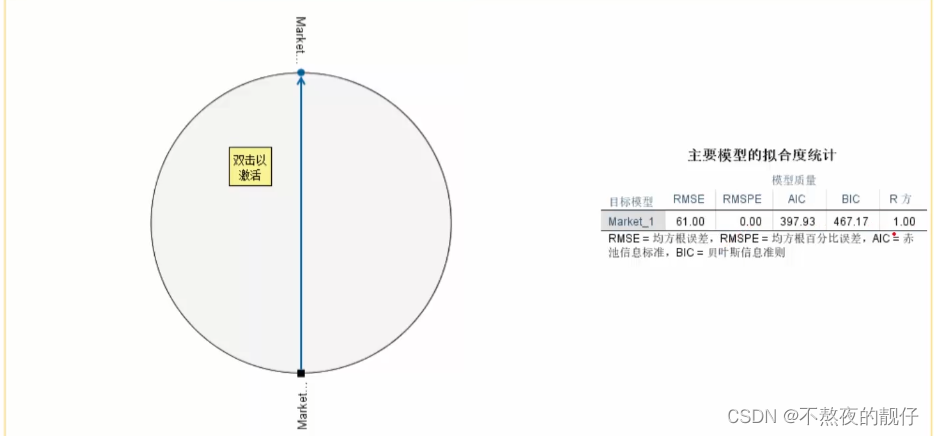
- 时间序列因果模型
-
Y
1
t
=
a
1
∗
Y
1
t
−
1
+
a
2
∗
Y
1
t
−
12
+
a
3
∗
Y
4
t
−
2
+
a
4
∗
Y
2
t
−
12
+
a
0
Y_{1_t}=a_1*Y_{1_{t-1}}+a_2*Y_{1_{t-12}}+a_3*Y_{4_{t-2}}+a_4*Y_{2_{t-12}}+a0
Y1t=a1∗Y1t−1+a2∗Y1t−12+a3∗Y4t−2+a4∗Y2t−12+a0


-
Y
1
t
=
a
1
∗
Y
1
t
−
1
+
a
2
∗
Y
1
t
−
12
+
a
3
∗
Y
4
t
−
2
+
a
4
∗
Y
2
t
−
12
+
a
0
Y_{1_t}=a_1*Y_{1_{t-1}}+a_2*Y_{1_{t-12}}+a_3*Y_{4_{t-2}}+a_4*Y_{2_{t-12}}+a0
Y1t=a1∗Y1t−1+a2∗Y1t−12+a3∗Y4t−2+a4∗Y2t−12+a0








 本文深入探讨了统计分析的各种方法,包括单样本和独立样本T检验、方差齐性检验、配对样本T检验、非参数检验以及多因素分析。在模型构建方面,讲解了线性回归、逻辑回归和时间序列分析,如ARIMA模型的选择和评估。此外,还涉及因子分析、共线性问题以及变量选择策略,强调了模型解释性和有效性的关键指标。
本文深入探讨了统计分析的各种方法,包括单样本和独立样本T检验、方差齐性检验、配对样本T检验、非参数检验以及多因素分析。在模型构建方面,讲解了线性回归、逻辑回归和时间序列分析,如ARIMA模型的选择和评估。此外,还涉及因子分析、共线性问题以及变量选择策略,强调了模型解释性和有效性的关键指标。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








