前缀树 字典树 ＋ 例题

前缀：

我们假定一个字符串：abgh，那么abgh就有4个前缀：a，ab，abg，abgh。

字符串：jhktgr，有6个前缀：j，jh，jhk，jhkt，jhktg，jhktgr。

前缀树：

对于上面两个字符串，我们可以做成一个树结构来表示它们：

这就是前缀树，每个边代表一个字符

还有一种特殊情况：我们假设有2个字符串：abcde，abcdefg。那么它们的前缀树应该如下表示：

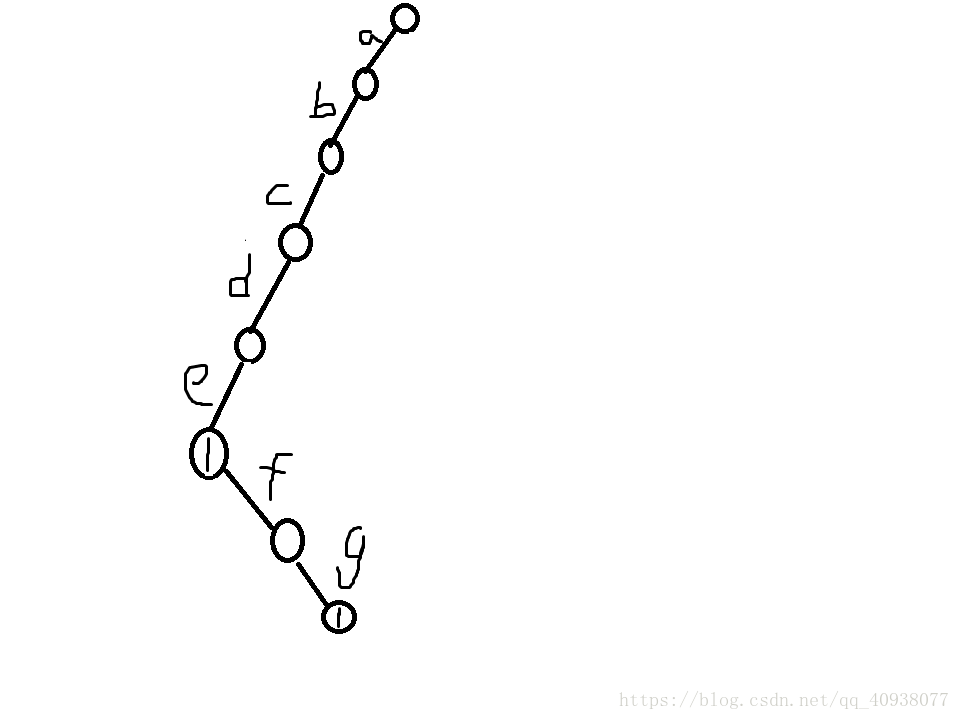
前缀树的实现：

对于每个节点，我们可以往其中加入数据项，具体问题具体加不同含义的数据项，这里我们只讲2个基本的数据项

数据项一：以当前节点所代表字符为结束字符的字符串有几个，上图中e的代表节点上的1和g的代表节点上的1都是这个意思，代表有一个字符串是以e字符结束的，有一个字符串是以g字符结束的。

数据项二：有多少个字符串划过当前节点所代表的字符，上图中没有写出来，但是a，b，c，d，e的代表节点上的该数据项都是2，f，g的代表节点上的该数据项都是1。

基本函数：

一：insert(string str)函数，建树，将str字符串加入到前缀树中去

二：search(string str)函数，查询所有字符串中有几个str字符串

三：delete(string str)函数，删除前缀树中str字符串

四：strfixnumber(string str)函数，查询有多少个字符串是以str字符串为前缀的

代码实现：

#include<bits/stdc++.h>
using namespace std;
class node
{
public:
    int End;//以当前字符为结尾的字符串的个数
    int after;//当前节点被划过了多少次
    map < char , node* > next;
    node()//构造函数，给每个数据项赋初值
    {
       End=0;
       after=0;
    }
};
class trie
{
private:
    node* root;
public:
    void Insert(string str)//建树操作,将字符串str加入到前缀树中去
    {
        node* heap=root;//通过heap节点不断的往树下走，建树
        for(int i=0;i<str.size();i++)
        {
            if(heap->next[str[i]]==NULL)//只要str字符串的当前字符在数中没有被建过，就建出来（就相当于给map的key赋一个node类型的节点）
            {
                node* z;
                heap->next[str[i]]=z;
            }
            heap=heap->next[str[i]];//让heap节点往树下走，继续建树
            heap->after++;//经过了这个点一次。after＋1
        }
        heap->End++;//str字符串遍历完了，end＋1
    }
    int Search(string str)//查找str字符串在前缀树中出现了几次
    {
        node* heap=root;//还是从头节点往树下走
        for(int i=0;i<str.size();i++)
        {
            if(heap->next[str[i]]==NULL)//只要这个条件满足，说明前缀树中不存在str字符串，直接返回0
                return 0;
            heap=heap->next[str[i]];//上面条件没有满足，heap节点继续往树下走
        }
        return heap->End;//最后返回end
    }
    void Delete(string str)//删除前缀树中str字符串
    {
        node* heap=root;//还是从头节点开始往树下走
        for(int i=0;i<str.size();i++)
        {
            heap=heap->next[str[i]];
            if(--heap->after==0)//如果前缀树中就有一个str字符串，那么只要访问str字符串的第一个字符就行，剩下的不用访问，直接删除就行了
            {
                heap->next[str[i]]=NULL;
                return ;
            }
        }
        heap->End--;//如果程序到达了这里，说明前缀树中有str字符串，最后end减1
        return ;
    }
    int strfixnumber(string str)//查询有多少个字符串是以str字符串为前缀的
    {
        node* heap=root;
        for(int i=0;i<str.size();i++)
        {
            if(heap->next[str[i]]==NULL)//前缀树中直接没有str字符串，肯定没有以str字符串为前缀的字符串
                return 0;
            heap=heap->next[str[i]];
        }
        return heap->after;
    }
};
int main()
{

}

例题一：HDU【4825】

http://acm.hdu.edu.cn/showproblem.php?pid=4825

题意：

给出n个数和m次询问，对于每次询问给出一个数x，问在n个数中哪个数与x异或值最大

思路：

首先看异或的性质，1&1=0    0&0=0   1&0=1  0&1=1。总结一下，就是相等为0，不相等为1。所以对于高位来说，尽量让数字不相等，这样才能够使得异或和大。我们将这n个数的二进制建成一个字典树，每个数的二进制的高位在根部，低位在叶部，然后从x的二进制的高位往低位遍历，尽量不走数字相等的路径，最后到达叶子节点后所代表的10进制数就是我们的答案。

代码：

#include<bits/stdc++.h>
using namespace std;
int jieguo[100001];
int t,n,m;
struct node
{
    int original;//这个值代表二进制串到这结束后所表示的十进制的数字
    node* next1[2];
    node()//构造函数，初始化
    {
        original=0;
        for(int i=0;i<2;i++)
            next1[i]=NULL;
    }
};
void Insert(node *root,int z)//建树操作
{
    int num=z;
    node* heap=root;//通过heap节点不断的往树下走，建树
    for(int i=31;i>=0;i--)//二进制最多有32位，我们从高位往低位建，把这32为全部建出来
    {
        int bit = (num >> i) % 2; //这是从高位往低位求出某个数的二进制的方法，相当于一个模板
        if(heap->next1[bit]==NULL)//如果当前位数上为空，就建出来
            heap->next1[bit]=new node();
        heap=heap->next1[bit];//让heap节点往树下走，继续建树
    }
    heap->original=z;
}
int core(node *root,int num)//这是匹配的函数
{
    node* heap=root;
    for(int i=31;i>=0;i--)//这次求给定的数的二进制
    {
        int index = (num >> i) & 1;//得到给定的数的相应位数上的二进制数
        if(heap->next1[!index]!=NULL)//我们要求高位上的数字尽量不一样（可以一样，这个地方相当于一个贪心），如果存在数字不一样的这条路，我们就走这条路
            heap=heap->next1[!index];
        else                         //不存在数字不一样的这条路，我们走数字一样的路
            heap=heap->next1[index];
    }
    return heap->original;//最后返回我们走过的这条路所代表的10进制的数
}
int main()
{
    scanf("%d",&t);
    int l=1;
    while(t--)
    {
        node* root = new node();
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++)
        {
            int ans;
            scanf("%d",&ans);
            Insert(root,ans);
        }
        int p;
        int Jie_Size=0;
        for(int i=0;i<m;i++)
        {
            scanf("%d",&p);
            jieguo[Jie_Size++]=core(root,p);//将计算得到的结果存到结果数组中去
        }
        printf("Case #%d:\n",l++);
        for(int i=0;i<Jie_Size;i++)
            printf("%d\n",jieguo[i]);
    }
}

例题二：poj[3764]

http://poj.org/problem?id=3764

题意：

给出一棵树，求树中最长的xor路径。（n<=100000）

输入 点的数量n,之后n-1行代表x点到y点间有一条权值为z的边；

输出 最优解；

思路：

https://www.cnblogs.com/phile/p/4473138.html

https://www.cnblogs.com/Alan-Luo/articles/9102805.html

首先，深搜求出某个点到每个点的XOR路径，然后把求出来的数都按二进制一位一位存到trie树里面，之后枚举所有的点，对于当前枚举的点，一位一位地去找出哪个点和当前枚举的点所构成的路径上的权值的XOR和最大，这道题完美地走向结局。

还有一点，写得稍微简单一点，不然容易被卡时限。我的代码就卡时限了，不过我不想改了，思路肯定是正确的。

代码：

#include<algorithm>
#include<iostream>
#include<limits.h>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
typedef long long ll;
using namespace std;
int n;
int u[330000],v[330000],w[330000],Frist[330000],Next[330000];
int Exclusive[330000],visited[330000];//Exclusive[i]代表从0点到i点的异或和，visited[i]是标记数组，用于深搜
struct Node
{
    int original;
    Node *next1[2];
    Node()
    {
        original=0;
        for(int i=0;i<2;i++)
            next1[i]=NULL;
    }
};
void add(int u1,int v1,int w1,int i)
{
    Next[i]=Frist[u1];
    Frist[u1]=i;
}
void Insert(Node *root,int num)//往字典树中加入num的二进制
{
    int numz=num;
    Node *heap=root;
    for(int i=31;i>=0;i--)
    {
        int bit=(num>>i)%2;
        if(heap->next1[bit]==NULL)
            heap->next1[bit]=new Node();
        heap=heap->next1[bit];
    }
    heap->original=numz;
}
int Find(Node *root,int num)//在字典树中寻找和num异或最大的那个数，并且返回
{
    Node *head=root;
    for(int i=31;i>=0;i--)
    {
        int bit=(num>>i)%2;
        if(head->next1[!bit]!=NULL)
            head=head->next1[!bit];
        else
            head=head->next1[bit];
    }
    return head->original;
}
void dfs(int head,int sum)//深搜，这个函数求的是head节点到其余各个节点的异或和，存在Exclusive数组中
{
    int p=Frist[head];
    while (p!=-1)
    {
        if(!visited[v[p]])//如果这个点没有被访问过，访问这个点
        {
            visited[v[p]]=true;
            Exclusive[v[p]]=sum xor w[p];//这是异或和的求法
            dfs(v[p],Exclusive[v[p]]);
        }
        p=Next[p];
    }
}
int main()
{
    memset(visited,false,sizeof(visited));
    memset(Frist,-1,sizeof(Frist));
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        scanf("%d%d%d",&u[i],&v[i],&w[i]);
        add(u[i],v[i],w[i],i);
    }
    dfs(0,0);
    Node *root=new Node();
    for(int i=0;i<n;i++)
        Insert(root,Exclusive[i]);
    int ans=INT_MIN;
    for(int i=0;i<n;i++)//遍历每一个数，找到与这个数异或和最大的数，取其中的最大值就是结果
        ans=max(ans,Find(root,Exclusive[i]));
    printf("%d\n",ans);
}

例题三：HDU【5536】

http://acm.hdu.edu.cn/showproblem.php?pid=5536

题意：

有一个数组a[], 包含n个数，从n个数中找到三个数使得 (a[i]+a[j])⊕a[k]最大，i,j,k不同

思路：

https://www.cnblogs.com/zhengguiping--9876/p/5876227.html

运用0 1字典树来做，我们先将所有的数的二进制放入到字典树中去，然后枚举a[i]和a[j]，对于枚举的每个a[i]和a[j]，我们先从字典树中暂时删除a[i]和a[j]，然后进行查询，找到和a[i]+a[j]异或值最大的a[k]，然后将a[i]和a[j]重新插入到字典树中去，维护最大值就是结果。

代码：

#include<algorithm>
#include<iostream>
#include<limits.h>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
typedef long long ll;
using namespace std;
int t,n;
int root[1007];
struct Node
{
    int value;//当前节点所代表的数字划过了value次
    int original;//当前路径所代表的十进制数字，只有叶子节点才有有意义的original，其余节点的original值都是0
    Node *next1[2];
    Node()
    {
        value=0;
        original=0;
        for(int i=0;i<2;i++)
            next1[i]=NULL;
    }
};
void Insert(Node *head,int num)//插入操作
{
    Node *root=head;
    for(int i=31;i>=0;i--)
    {
        int bit=(num>>i)%2;//获得num当前位数的二进制数字
        if(root->next1[bit]==NULL)//如果为空，就建出来
            root->next1[bit]=new Node();
        root=root->next1[bit];
        root->value++;//这个地方代码的顺序，root->value这句代码必须在root=root->next1[bit]这句代码之后
    }
    root->original=num;
}
void Delete(Node *head,int NumberDelete)//这是删除操作
{
    Node *root=head;
    for(int i=31;i>=0;i--)
    {
        int bit=(NumberDelete>>i)%2;
        root=root->next1[bit];
        root->value--;//划过的次数减一
    }
}
int query(Node *head,int Number_query)//查询操作
{
    Node *root=head;
    int ans=0;
    for(int i=31;i>=0;i--)
    {
        int bit=(Number_query>>i)%2;
        if((root->next1[!bit]!=NULL)&&(root->next1[!bit]->value>0))//如果这个条件满足，说明我们想要走的路径可以走
            root=root->next1[!bit];
        else
            root=root->next1[bit];
    }
    return root->original^Number_query;//返回最大的异或值
}
int main()
{
    scanf("%d",&t);
    while (t--)
    {
        Node *head=new Node();
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&root[i]);
            Insert(head,root[i]);
        }
        int ans=-1;
        for(int i=1;i<n;i++)//枚举所有的想加的两个值
        {
            for(int j=i+1;j<=n;j++)
            {
                Delete(head,root[i]);//先删除这两个值
                Delete(head,root[j]);
                ans=max(ans,query(head,root[i]+root[j]));//查询
                Insert(head,root[i]);//再将这两个值放回到字典树中去
                Insert(head,root[j]);
            }
        }
        printf("%d\n",ans);
    }
}