计蒜客暑假集训第一阶段第四场 b题

最新推荐文章于 2021-05-27 16:57:51 发布

一枚研究生er

最新推荐文章于 2021-05-27 16:57:51 发布

阅读量620

点赞数

分类专栏：算法习题

本文链接：https://blog.csdn.net/qq_40938077/article/details/81271624

版权

算法习题专栏收录该内容

34 篇文章 2 订阅

订阅专栏

Bahiyyah has a convex polygon with nn vertices P_0, P_1, \cdots, P_{n-1}P0,P1,⋯,Pn−1 in the counterclockwise order.Two vertices with consecutive indexes are adjacent, and besides, P_0P0 and P_{n-1}Pn−1 are adjacent.She also assigns a point QQ inside the polygon which may appear on the border.

Now, Bahiyyah decides to roll the polygon along a straight line and calculate the length of the trajectory (or track) of point QQ.

To help clarify, we suppose P_n = P_0, P_{n+1} = P_1Pn=P0,Pn+1=P1 and assume the edge between P_0P0 and P_1P1 is lying on the line at first.At that point when the edge between P_{i-1}Pi−1 and P_iPi lies on the line, Bahiyyah rolls the polygon forward rotating the polygon along the vertex P_iPi until the next edge (which is between P_iPi and P_{i+1}Pi+1) meets the line.She will stop the rolling when the edge between P_nPn and P_{n+1}Pn+1 (which is same as the edge between P_0P0 and P_1P1) meets the line again.

Input Format

The input contains several test cases, and the first line is a positive integer TT indicating the number of test cases which is up to 5050.

For each test case, the first line contains an integer n~(3\le n \le 50)n (3≤n≤50) indicating the number of vertices of the given convex polygon.Following nn lines describe vertices of the polygon in the counterclockwise order.The ii-th line of them contains two integers x_{i-1}xi−1 and y_{i-1}yi−1, which are the coordinates of point P_{i-1}Pi−1.The last line contains two integers x_QxQ and y_QyQ, which are the coordinates of point QQ.

We guarantee that all coordinates are in the range of -10^3−103 to 10^3103, and point QQ is located inside the polygon or lies on its border.

Output Format

For each test case, output a line containing Case \#x: y, where xx is the test case number starting from 11, and yyis the length of the trajectory of the point QQ rounded to 33 places.We guarantee that 44-th place after the decimal point in the precise answer would not be 44 or 55.

Hint

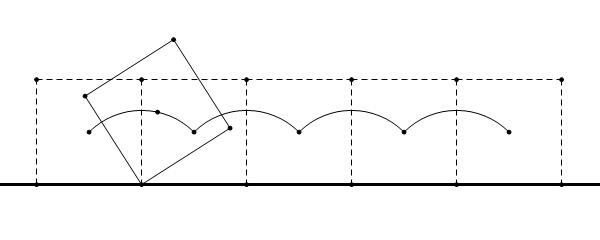
The following figure is the the trajectory of the point QQ in the first sample test case.

样例输入

样例输出

Case #1: 8.886
Case #2: 7.318
Case #3: 12.102
Case #4: 14.537

题目大意：

按照逆时针绕向给出一个凸多边形的 n 个顶点 P0,P1,··· ,Pn−1，再给出凸多边形内部（含边界）一点 Q。现在要将这个凸多边形在地上无滑动地滚动一周，初始时 P0P1 边与地面接触，假设当前是 PiP(i+1) mod n 边与地面接触，那么滚动一下之后则是 P(i+1) mod nP(i+2) mod n 边与地面接触。不难发现，从初始状态滚动 n 下之后 P0P1 边再一次与地面接触，这时认为凸多边形已经滚动了一周。现在你需要求出凸多边形滚动一周之后点 Q 经过的轨迹长度。输入格式第一行包含一个整数 T，表示测试数据的组数。
接下来依次描述 T 组测试数据。对于每组测试数据：
第一行包含一个整数 n，表示凸多边形的顶点数。接下来 n 行，每行包含两个整数 xPi,yPi，按照逆时针的顺序给出凸多边形 n 个顶点 P1,P2,··· ,Pn 的坐标。
最后一行包含两个整数 xQ,yQ，表示点 Q 的坐标。
保证点 Q 在凸多边形内部（含边界）。
输出一行信息 "Case #x: y"（不含引号），其中 x 表示这是第 x 组测试数据， y 表示凸多边形滚动一周之后点 Q 经过的轨迹长度，四舍五入精确到小数点后 3 位，数据保证答案的小数点后第 4 位不是 4 或 5。

解题思路：

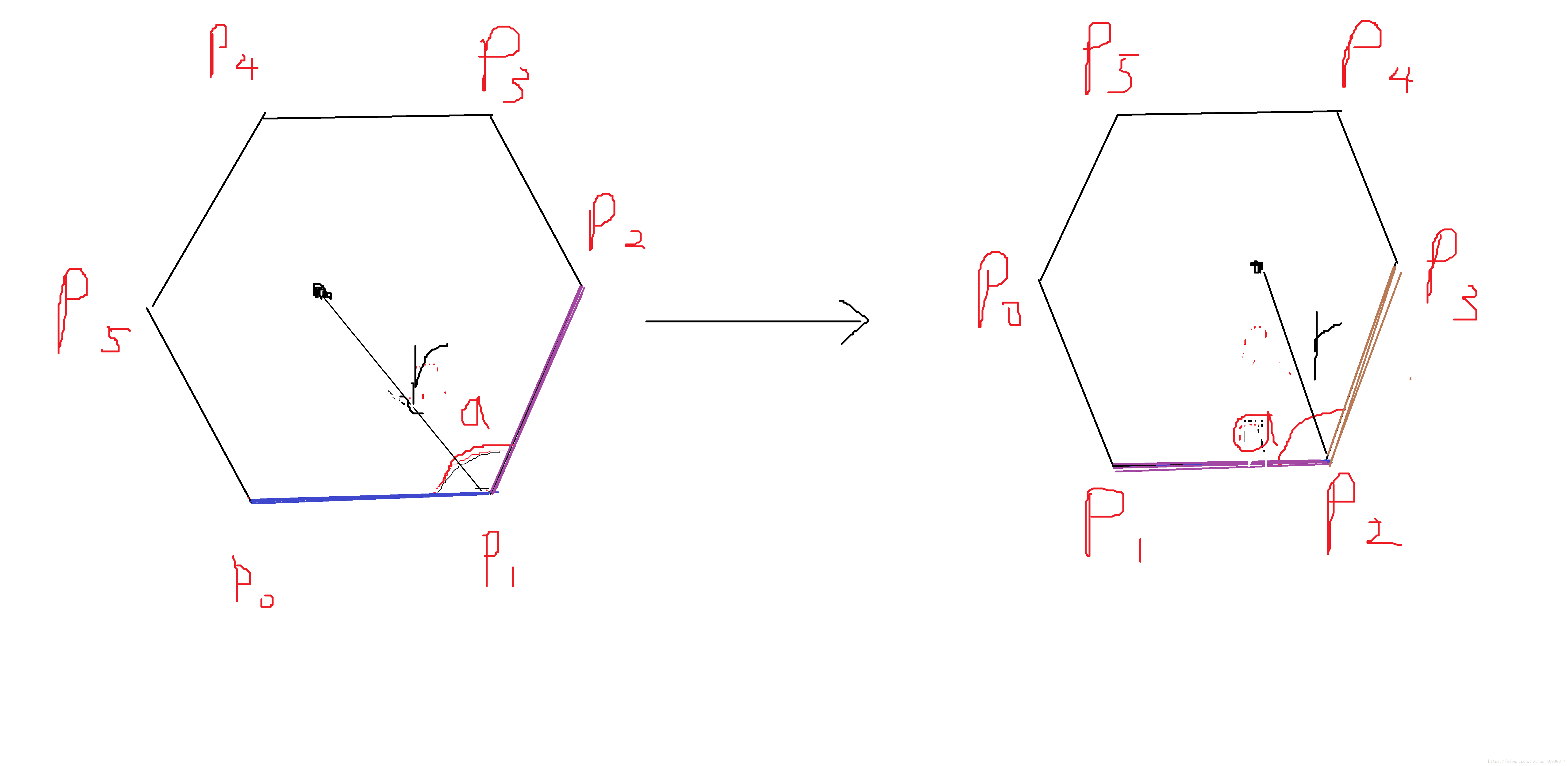
假设每次着地的边和该边的右边相邻的一条边所形成的夹角为a。

通过观察发现，给定的点所走的路径是n个圆弧，圆心角是π-a，半径r为给定的点到两边的交点的距离。我们可以通过弧长公式来计算出给定的点的路径（圆弧）。因为题目说当刚开始运动时着地的边再一次着地后，运动停止，那么就可以确定圆弧一共有n个（每次圆弧的长度可能不一样），所以累加n次计算出的结果就行了。

代码：

#include<bits/stdc++.h>
#define pai 3.1415926535898
using namespace std;
int n;
int a[51][2];
int x,y;
int t;
double sum=0;
double dis(int x1,int y1,int x2,int y2)//计算a(x1,y1)和b(x2,y2)两点之间的距离
{
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main()
{
    cin>>t;
    int l=1;
    while (t--)
    {
        cin>>n;
        for(int i=0;i<n;i++)
            cin>>a[i][0]>>a[i][1];
        cin>>x>>y;
        int visited[3];//visited数组存的三个数依次是着地的那条边的第一个顶点，第二个顶点和第二个顶点所在的另一条边的另一个顶点
        visited[0]=0;//初始化为0,1,2
        visited[1]=1;
        visited[2]=2;
        double r=0,o=0;//r代表半径，o代表圆心角的弧度制
        int z1=n-1;
        while (n--)
        {
            double z=pow((x-a[visited[1]][0]),2)+pow((y-a[visited[1]][1]),2);
            r=sqrt(z);//算出半径，用给定的点和三个点中的中间的点来算（两点间距离公式）
            double t1=dis(a[visited[0]][0],a[visited[0]][1],a[visited[1]][0],a[visited[1]][1]);//t1代表第一个顶点和第二个顶点所连出来的边的长度
            double t2=dis(a[visited[1]][0],a[visited[1]][1],a[visited[2]][0],a[visited[2]][1]);//t2代表第二个顶点和第三个顶点所连出来的边的长度
            double t3=dis(a[visited[0]][0],a[visited[0]][1],a[visited[2]][0],a[visited[2]][1]);//t3代表第三个顶点和第一个顶点所连出来的边的长度
            o=acos((t1*t1+t2*t2-t3*t3)/(2*t1*t2));//之所以求t1，t2，t3是为了求出圆心角的弧度制
            sum+=r*(acos(-1.0)-o);//通过弧长公式累加结果，转化成180度弧度制
            if(visited[2]<z1)//更新下次所需要计算的三个点
            {
                visited[0]=visited[1];
                visited[1]=visited[2];
                visited[2]=visited[1]+1;
            }
            else if(visited[2]==z1)
            {
                visited[0]=visited[1];
                visited[1]=visited[2];
                visited[2]=0;
            }
        }
        cout<<"Case #"<<l++<<": ";
        printf("%.3f\n",sum);
        sum=0;
    }
}

新知识：

一：知道了acos函数，acos函数传入的是一个角度的余弦值，函数返回值是该角度的弧度制。

二：对于多次计算的题目，我们可以寻找规律来求解，一定会有规律的，不可能每次情况都不同，让你一次一次都求解出来。

一枚研究生er

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
计蒜客暑假集训第一阶段第四场 b题

Bahiyyah has a convex polygon with nn vertices P_0, P_1, \cdots, P_{n-1}P0,P1,⋯,Pn−1 in the counterclockwise order.Two vertices with consecutive indexes are adjacent, and besides, P_0P0 and P_{n-1...
复制链接

扫一扫