4椭圆曲线密码学：破坏安全性及与RSA的比较

社小雪

于 2021-07-21 21:38:00 发布

阅读量1.5k

点赞数 1

CC 4.0 BY-SA版权

文章标签：算法 python 人工智能 java 机器学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_40965639/article/details/119115454

本文是ECC系列的最后一篇，探讨了椭圆曲线离散对数问题的破解方法，包括baby-step giant-step算法和Pollard's rho方法。虽然这两种算法在实践中有效，但随着技术发展，如Shor's algorithm可能对未来加密安全性构成威胁。文章还比较了ECC与RSA的优劣，指出ECC在密钥长度和计算效率上的优势。同时，文章提出对NIST标准曲线可能存在的安全隐患的担忧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原文链接：https://andrea.corbellini.name/2015/06/08/elliptic-curve-cryptography-breaking-security-and-a-comparison-with-rsa/

这篇文章是ECC系列的第四篇，也是最后一篇。

在上一篇文章中，我们已经看到了两种算法，ECDH和ECDSA，我们也看到了椭圆曲线的离散对数问题是如何对其安全性起重要作用的。但是，如果你还记得，我们说过对于离散对数问题的复杂性我们没有数学证明：我们认为它是“困难的”，但我们不能确定。在这篇文章的第一部分，我们将试着了解在实践中使用今天的技术有多“困难”。

然后，在第二部分，我们将尝试回答这个问题：如果RSA(和其他基于模算术的密码系统)可以很好地工作，我们为什么需要ECC(椭圆曲线密码学)?

破解离散对数问题(Breaking the discrete logarithm problem)

现在我们将看到计算椭圆曲线离散对数的两种最有效的算法：the baby-step, giant-step algorithm和Pollard's rho method。

在开始之前，提醒一下，下面是离散对数问题的内容：给定两点P和Q，找出满足方程Q = xP的整数x。这些点属于椭圆曲线的一个子群，它有一个基点G，阶数为n。

Baby-step, giant-step

在输入算法细节之前，先快速考虑一下：我们总是可以将任意整数

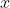This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

写成

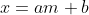This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

，其中a、m和b是三个任意整数。例如，我们可以写成10=2·3+4。

考虑到这一点，我们可以将离散对数问题的方程重写如下：

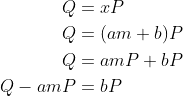
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

baby-step giant-step算法是一种“中间相遇”的算法。与暴力破解(逐个计算每一个

[公式]

来找到满足方程Q = xP要求的

[公式]

)相反，对于

[公式]

我们可以计算得更少，对于

[公式]

也可以计算得更少，直到我们找到一个满足条件的。算法的工作原理如下：

计算
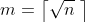
对
中的每一个b，计算

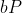并将结果存储在一个哈希表中
对
中的每一个a，：

　　　　　　(1)计算

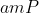
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

　　　　　　(2)计算

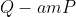
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

　　　　　　(3)检查哈希表，看看是否存在一个点bP使得

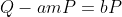
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

　　　　　　(4)如果这样的点存在，那么我们就找到了

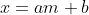
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

正如你所看到的，我们计算

[公式]

时的系数

[公式]

用很小的步长，但在第二部分当中，我们计算

[公式]

使用很大的步长，这两部分分别就是算法“baby”部分和“giant”部分。具体它可以如下图所示：

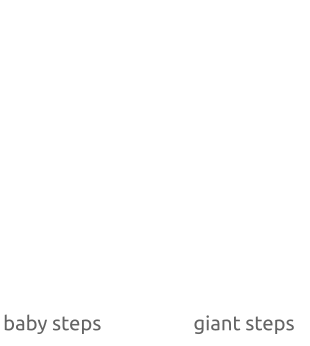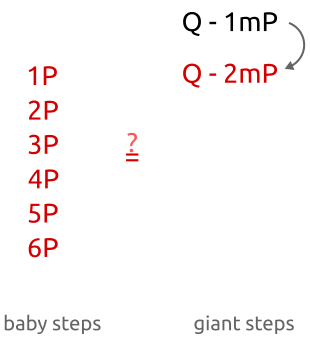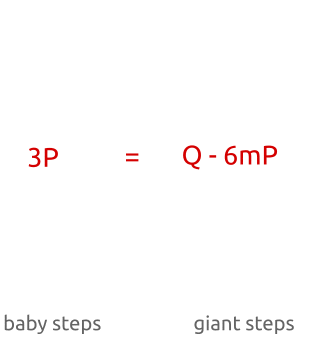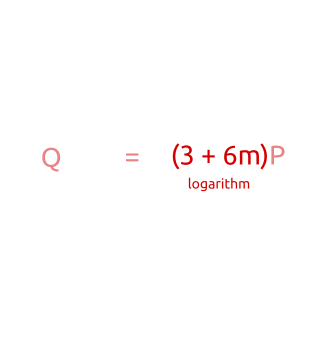
baby-step, giant-step算法：最初我们通过小步骤计算几个点，并将它们存储在一个哈希表中。然后我们执行大步骤，并将新点与哈希表中的点进行比较。一旦找到匹配，计算离散对数就是重新排列项的问题。

为了理解这个算法的原理，先暂时忘记这些被缓存的点

[公式]

，来看方程

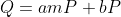This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

。看以下

最低0.47元/天解锁文章

200万优质内容无限畅学

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。