线性回归算法梳理

我想从一个链进行讲述：

一. 机器学习：

1.机器学习概念

在现实世界中我们是把我们人类的“经验”以数据的形式来存储，所以我们想着能不能让机器从这些数据进行学习，归纳中我们人类中的经验来进行推理。简称机器学习。
工程化定义：假设用P来评估计算机程序在某任务类T上的性能，若一个程序通过利用经验E在任务T上获得了性能改善，则我们就说关于T和P，该程序对E进行了学习。
人话就是：我们想让机器从我们这些人类的经验进行学习来帮我们解决一些任务，如果机器完成的不错，则我们会说机器从数据中得到了学习。
其中机器学习所研究的主要内容，是关于计算机从数据中产生“模型”的算法，也就是学习“算法”。所以说我们研究这些算法如何让机器更好地从数据中进行学习。

2.监督学习、无监督学习概念

监督学习、无监督学习的定义：
工程化定义：上面讲述的经验数据是否有任务对应的标记信息，有标记信息的是监督学习、没有是无监督学习。
人话就是：就是上面的数据，是有否任务对应的正确答案，例如一个与世隔绝的人在你面前，他一点都没见过这个世界，你想训练他适应社会，你想让他把你班同学分男、女两类。如果你和他说哪些是男同学哪些是女同学就是监督学习；如果没有和他说，让他凭自己的看到的感觉来分，那就是无监督学习。

3.泛化能力、偏差、方差概念

泛化能力，过拟合，欠拟合：
工程化定义：学得模型适用于新样本的能力，成为“泛化”能力。如果学得的能力在训练集的效果很好，测试集很差，是过拟合。如果学到的能力连在训练集的效果都很差的，是欠拟合
人话就是：接上面的例子，就是那个人学习完你和他说的男女分类任务之后，分辨不是你班同学的其他人的性别的能力，如果发现他分辨出你班同学的性别的能力很好，但是分辨其他人性别的能力，那就是过拟合；如果发现连你们同学性别都分辨不出来，那就是欠拟合

偏差：所有可能的训练数据集训练出的所有模型的输出的平均值与真实模型的输出值之间的差异，即刻画了学习算法本身的拟合能力； （偏差指的是模型在训练集上的错误率， 如5%。其实是与训练误差成线性关系的）
方差：不同的训练数据集训练出的模型输出值之间的差异，即刻画了数据扰动所造成的影响。（方差指的是模型在开发集（或测试集）上的表现与训练集上的差距。如开发集的错误率比训练集差1%。其实是与 测试误差 - 训练误差 成线性关系的。）

偏差、方差与过拟合、欠拟合的关系：
欠拟合：模型不能适配训练样本，有一个很大的偏差。
过拟合：模型很好的适配训练样本，但在测试集上表现很糟，有一个很大的方差。

3.过拟合、欠拟合的解决方法

当你发现你的模型的方差很高时，说明你的模型泛化能力弱，模型过拟合了，可以从以下几个角度分析：

1. 重新分析，清洗数据。 有时候，造成方差很大的原因往往是由于数据不良造成的，对于深度学习来说，有一个大规模，高质量的数据集是极为重要的。
2. 添加更多的训练数据。增大训练数据能够往往能够提高模型的泛化能力。
3. 加入正则化。正则化是机器学习中很重要的一个技巧，你必须掌握它。
4. 加入提前终止。意思就是在测试误差变化很慢甚至不变的时候可以停止训练，这项技术可以降低方差，但有可能增大了偏差。提前终止有助于我们能够在到达最佳拟合附近，避免进入过拟合状态。 通过特征选择减少输入特征的数量和种类。
5. 显著减少特征数量能够提高模型的泛化能力，但模型的拟合能力会降低，这意味着，该技术可以减小方差，但可能会增大偏差。不过在深度学习中，我们往往直接将所有特征放入神经网络中，交给算法来选择取舍。
6. 减少模型规模，降低模型复杂度（每层神经元个数/神经网络层数）： 谨慎使用。
7. 一般情况下，对于复杂问题如CV或NLP等问题不会降低模型复杂度，而对于简单问题，采用简单模型往往训练速度更快，效果很好。
8. 根据误差分析结果修改输入特征。 修改模型架构，使之更适合你的问题。 一般可以选择简单模型的情况下，不选择复杂模型。

当你发现你的模型的偏差很高时，这也意味着你的训练误差很高，模型欠拟合了，建议从以下几个角度试试：

1. 加大模型规模（更换其余机器学习算法，神经网络可以增加每层神经元/神经网络层数）：偏差很高很有可能是因为模型的拟合能力差，对于传统机器学习算法，各个方法的拟合能力不同，选择一个拟合能力更好的算法往往能够得出很好的结果。
2. 对于神经网络（拟合能力最强）而言，通过增加网络层数或增加每层单元数就能够很好的提高模型的拟合能力。
3. 根据误差分析结果来修改特征： 我们需要将错误样本分类，判断可能是由于什么原因导致样本失败，在针对分析结果，增加或减少一些特征。
4. 减少或去除正则化： 这可以避免偏差，但会增大方差。

4.交叉验证

在机器学习里，通常我们不能将所有的训练数据放到模型里面，否则我将没有多余的数据来评估这个模型的好坏。
有几种解决方法：

• 设置验证集，这是最常见的做法。就是把模型分成训练集和测试集，一般按照7：3来划分。我们用训练集来训练，用测试集来评估模型。
  可是存在两个弊端，
  1.最终模型与参数的选取将极大程度依赖于你对训练集和测试集的划分方法。为啥，我们可以看这一张图：
  
  右边是十种不同的训练集和测试集划分方法得到的test MSE曲线，可以看到在不同的划分方法下，test MSE的变动是很大的。所以如果我们的训练集和测试集的划分方法不够好，很有可能无法选择到最好的模型与参数。
  2.只用了部分数据进行模型的训练，无法充分利用数据。

所以提出了交叉验证
其中有一个K-fold Cross Validation，就是用多个数据作为测试集，其他的数据都作为训练集，具体的数目由K来决定。比如，如果K=5，那么我们利用五折交叉验证步骤就是：

1. 将所有数据集分成五分
2. 2.不重复地每次取一份做测试集，用其他四份做训练集来训练模型，之后计算该模型在测试集上$MS{E}_i$
3. 将5次的$MS{E}_i$取平均值得到最后的MSE
   通过交叉验证技术，可以不需要单独的验证集实现模型比较（用于模型选择和调整超参数），节省宝贵的训练数据。

二.线性回归的原理

按照维基百科的定义：
线性回归是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况成为简单回归，大于一个自变量情况的叫做多元回归。
公式如下:
$$f(x)=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$$
$x_i,b_i$分别对应的是输入的自变量（特征值），以及自变量对应的权重。

三.线性回归损失函数、代价函数、目标函数

由上面知道，数据集X是已知的，其中x对应的y也是已知的。我们就是试图让模型从数据(x,y)中学习到对应的权重w。
损失函数公式：
$$L(\theta )=|y_i-f(x_i)|$$一般针对单个样本 i
线性回归的损失函数：
$$(w_i^{\ast },b_i^{\ast })=argmin(y_i-w{x}_i-b{)}^2$$

代价函数公式：$$L(\theta )=1/N\ast \sum _{i=1}^N|y_i-f(x_i)|$$一般针对总体
线性回归的代价函数：$$(w^{\ast },b^{\ast })=argmin(1/(2\ast N)\ast \sum _{i=1}^N(y_i-w{x}_i-b))$$

目标函数公式：$$L(\theta )=1/N\ast \sum _{i=1}^N|y_i-f(x_i)|+正则化项$$
线性回归目标函数公式：$$(w^{\ast },b^{\ast })=1/(2\ast N)\ast \sum _{i=1}^N(y_i-f(x_i){)}^2+\lambda \sum _{i=1}^N({\theta }_j^2)$$
可能会奇怪正式的式子是绝对值，线性回归会用上平方和常数1/2，为了方便偏微分计算所以进行了优化，而且不影响我们找到模型的最佳w和b。

四优化方法：

1.梯度下降法
目标函数$L(\theta )$关于参数$\theta$的梯度将是目标函数上升最快的方向。对于最小化优化问题，只需要将参数沿着梯度相反的方向迈一步，就可以实现目标函数的下降，其中有一个学习率$\alpha$，他决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
公式：
$$\theta =\theta -\alpha \frac{1}{N}{\nabla }_{\theta }L(\theta )$$
$${\nabla }_{\theta }L(\theta )=\frac{df(\theta )}{d\theta }$$
通过这样不断优化得到最佳的w和b。

2.牛顿法
牛顿法不仅可以用来求解函数的极值问题，还可以用来求解方程的根，二者在本质上是一个问题，因为求解函数极值的思路是寻找导数为0的点。
和梯度下降法一样，牛顿法也是寻找导数为0的点，同样是一种迭代法，核心思想是在某点处用二次函数来近似目标函数，得到导数为0的方程，求解该方程，从而得到下一个迭代的点，通过这样反复迭代，直到达到导数为0的点处（因为是用二次函数近似，因此可能会有误差）。
我们先进一元函数的情况，然后推广到多元函数。
一元函数的情况
根据一元函数的泰勒展开公式，我们对目标函数在$x_0$(随机选取或者某种方法确定)点处做泰勒展开，有:
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{1}{2}{f}^{\prime \prime }(x_0)(x-x_0{)}^2+...+\frac{1}{n!}{f}^n(x_0)(x-x_0{)}^n...$$
忽略2次以上的项则有：
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{1}{2}{f}^{\prime \prime }(x_0)(x-x_0{)}^2$$
然后我们在$x_0$点处，要以它为基础，找到导数为0的点，即导数为0。对上面等式两边同时求导，并令导数为0，可以得到下面的方程：
$$f^{\prime }(x)=f^{\prime }(x_0)+f^{\prime \prime }(x_0)(x-x_0)=0$$
可以解得：
$$x=x_0-\frac{f^{\prime }(x_0)}{f^{\prime \prime }(x_0)}$$
这样我们就得到了下一点的位置，从而走到$x_1$.。接下来重复这个过程，直到到达导数为0的点，由此得到牛顿法的迭代公式：
$$x_{t+1}=x_t-\frac{f^{\prime }(x_t)}{f^{\prime \prime }(x_t)}$$
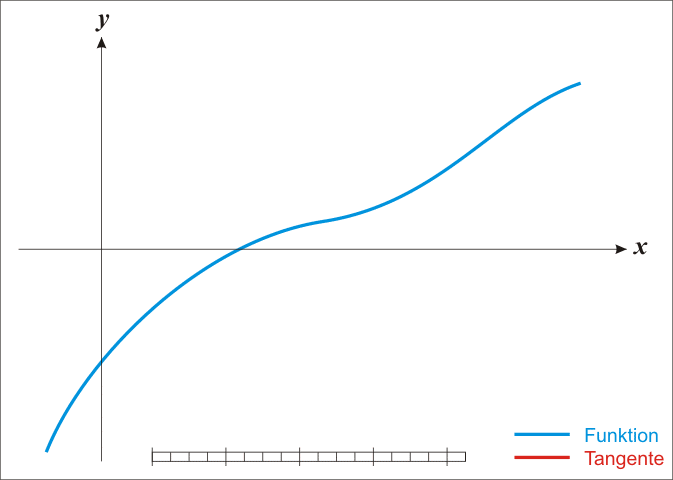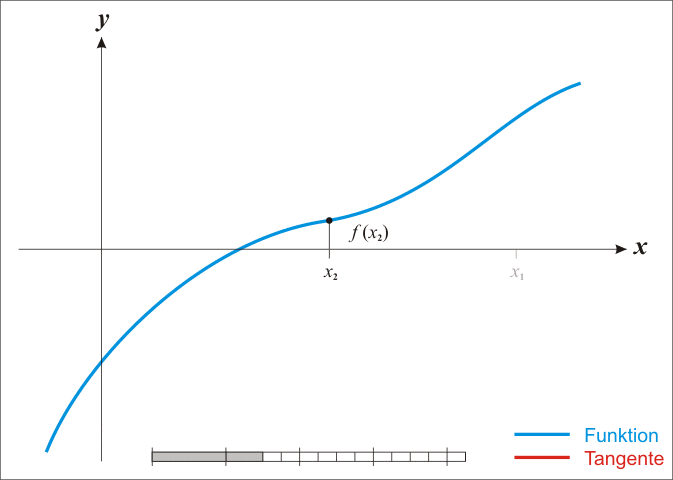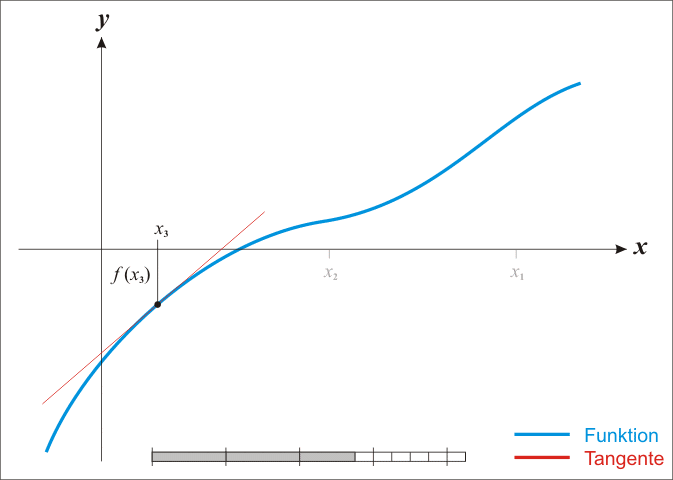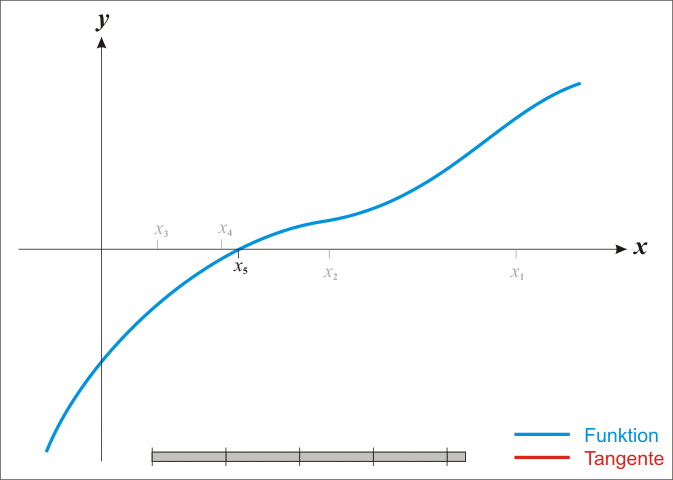
总结：初始迭代点$x_0$，反复用上面的公式进行迭代，直到达到导数为0的点或者达到最佳迭代次数。可以看看这个动图来体会

二元函数的情况
下面的讲解需要对Hessian的概念有着先验的了解。
根据多元函数的泰勒展开公式，我们对目标函数在$x_0$点处做泰勒展开，有：
$$f(x)=f(x_0)+\nabla f(x_0{)}^T(x-x_0)+\frac{1}{2}(x-x_0{)}^T{\nabla }^{2}f(x_0)(x-x_0)+o((x-x_0{)}^2)$$
忽略二次及以上的项，并对上式两边同时求梯度，得到函数的导数（梯度向量）为：
$$\nabla (x)=\nabla f(x_0)+{\nabla }^{2}f(x_0)(x-x_0)$$
其中${\nabla }^{2}f(x_0)$即为Hessian矩阵，在后面我们写成H。令函数梯度为0，则有：
$$\nabla f(x_0)+{\nabla }^{2}f(x_0)(x-x_0)=0⟹x=x_0-({\nabla }^{2}f(x_0){)}^{-1}\nabla f(x_0)$$
这是一个线性方程组的解。如果将梯度向量简写为g，上面的公式可以简写为：
$$x=x_0-H^{-1}g$$
从初始点$x_0$开始，反复计算函数在$x_0$处的Hessian矩阵和梯度向量，然后用下述公式进行迭代：
$$x_{k+1}=x_k-H_k^{-1}{g}_k$$
最终会到达函数的驻点处。其中$-H^{-1}g$称为牛顿方向。迭代终止的条件是梯度的模接近于0，然后函数值下降小于指定阈值。

2.拟牛顿法
牛顿法在每次迭代时需要计算出Hessian矩阵，然后求解一个以该矩阵为系数矩阵的线性方程组，这非常耗时，另外Hessian矩阵可能不可逆。为此提出了一些改进的方法，典型的代表是拟牛顿法(Quasi-Newton).
拟牛顿法的思想是不计算目标函数的Hessian矩阵然后求逆矩阵，而是通过其他手段得到Hessian矩阵或其逆矩阵的近似矩阵。具体做法是构造一个近似Hessian矩阵或其逆矩阵的正定对称矩阵，用该矩阵进行牛顿法的迭代。将函数在$x_{k+1}$点出进行泰勒展开，忽略二次以上的项，有：
$$f(x)\approx f(x_{k+1})+\nabla f(x_{k+1}{)}^T(x-x_{k+1})+\frac{1}{2}(x-x_{k+1}{)}^T{\nabla }^{2}f(x_{k+1})(x-x_{k+1})$$
对上式两边同时去梯度，有：
$$\nabla f(x)\approx \nabla f(x_{k+1})+{\nabla }^{2}f(x_{k+1})(x-x_{k+1})$$
令$X=X_k$，有：
$$\nabla f(x_{k+1})-\nabla f(x_k)\approx {\nabla }^{2}f(x_{k+1})(x_{k+1}-x_k)$$
这可以简写为：
$$g_{k+1}-g_k\approx H_{k+1}(x_{k+1}-x_k)$$
如果令：
$$s_k=x_{k+1}-x_k$$
$$y_k=g_{k+1}-g_k$$
上式可以简写为：
$$y_k=H_{k+1}{s}_k$$
即：
$$s_k\approx H_{k+1}^{-1}{y}_k$$
根据此条件，构造出了多种拟牛顿法，典型的有DFP算法、BFGS算法、L-BFGS算法等，在这里我们重点介绍BFGS算法。下图列出了常用的拟牛顿法的迭代公式：

BFGS算法是它的四个发明人Broyden，Fletcher，Goldfarb和Shanno名字首字母的简写。算法的思想是构造Hessian矩阵的近似矩阵：
$$B_k\approx H_k$$
并迭代更新这个矩阵：
$$B_{k+1}=B_k+\Delta B_k$$
该矩阵的初始值$B_0$为单位阵l。这样，要解决的问题就是每次的修正矩阵$\Delta B_k$的构造。其计算公式为：
$$\Delta B_k=\alpha u{u}^T+\beta v{v}^T$$
其中：
$$u=y_k$$
$$v=B_k{s}_k$$
$$\alpha =\frac{1}{y_k^T{s}_k}$$
$$\beta =-\frac{1}{s_k^T{B}_k{s}_k}$$
因此有
$$\Delta B_k=\frac{y_k{y}_k^T}{y_k^T{s}_k}-\frac{B_k{s}_k{s}_k^T{B}_k}{s_k^T{B}_k{s}_k}$$
因此算的的完整流程为：
1.给定的优化变量的初始值$x_0$和精度阈值$\epsilon$，令$B_0=I,K=0$
2.确定搜索方向$d_k=-B_k^{-1}{g}_k$
3.搜索得到步长${\lambda }_k$，令$S_k={\lambda }_k{d}_k,X_{k+1}=X_k+S_k$
4.如果$$||g_{k+1}||<\epsilon$$，则迭代结束
5.计算$Y_k=g_{k+1}-g_k$
6.计算$B_{k+1}=B_k+\frac{Y_k{y}_k^T}{Y_k^Y{S}_k}-\frac{B_k{S}_k{S}_k^T{B}_k}{S_k^T{B}_{k}x{S}_k}$
7.令K=K+1,返回步骤2
每一步迭代需要计算nxn的矩阵$D_k$，当n很大时，存储改矩阵非常损耗内存。为此提出了改进方法L-BFGS，其思想是不存完整的矩阵$D_k$，只存储向量$S_k$和$Y_k$。

五 线性回归的评估指标：

1.MSE RMSE

对模型的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要衡量模型泛化能力的评价标准，这就是评估指标。我们需要根据任务的需求来确定评价标准。
在预测任务中，给定样例集D={$(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$}，其中$y_i$是示例$x_i$的真实标记。要评估模型f的性能，就要把学习期预测结果f(x)与真实标记y进行比较。
回归任务最常用的性能度量是“均方误差”(mean squared error)
$$E(f;D)=\frac{1}{m}\sum _{i=1}^n(f(x_i)-y_i{)}^2$$
更一般的，对于数据分布D和概率密度函数$p(\cdot )$，均方误差课描述为：
$$E(f;D)={\int }_{x\in D}(f(x)-y{)}^{2}p(x)dx$$

但有一个问题，之前为了保证式子每项为正且可导（所以没用绝对值的表示方式），我们对市值式子加了一个平方，但会引入量纲的问题，如房子价格为万元，平方后就成了万元的平方。

于是需要改进，对MSE开方，使量纲相同，得到均方根误差RMSE(Root Mean Squared Error)

MSE与RMSE的区别仅在于对量纲是否敏感

又一标准，通过加绝对值，即平均绝对误差 MAE(Mean Absolute Error)

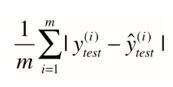
RMSE 与 MAE 的量纲相同，但求出结果后我们会发现RMSE比MAE的要大一些。这是因为RMSE是先对误差进行平方的累加后再开方，它其实是放大了较大误差之间的差距。而MAE反应的就是真实误差。因此在衡量中使RMSE的值越小其意义越大，因为它的值能反映其最大误差也是比较小的。

2. 衡量线性回归最好的指标：R平方(R Squared)

对于上述的衡量方法，如RMSE和MAE还是有问题的，还是因为量纲不一样。比如我们预测考试分数误差是10，预测房价误差是1w。但我们却不能评价我们的模型是更适合预测分数还是预测房价。
解决方案：新的指标——R方



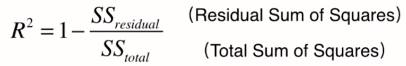
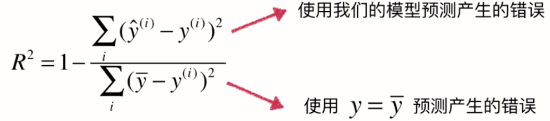
R方将回归结果归约到了0~1间，允许我们对不同问题的预测结果进行比对了。

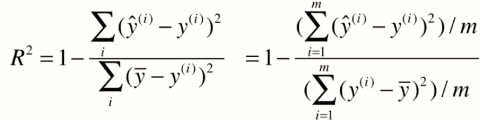
我们可发现，上面其实就是MSE，下面就是方差

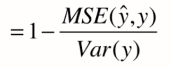
六 sklearn参数详解：

from sklearn import linear_model

导入linear_model模块，然后创建一个线性模型linear_model.LinearRegression，该线性回归模型创建有几个参数（可以通过help(linear_model.LinearRegression)来查看）：

1. fit_intercept：bool量，选择是否需要计算截距，默认为True，如果中心化了的数据可以选择false
2. normalize：bool量，选择是否需要标准化（中心化），默认为false，和参数fit_intercept有关，自行思考
3. copy_x:bool量，选择是否幅值X数据，默认True,如果否，可能会因为中心化把X数据覆盖
4. n_job:int量，选择几核用于计算，默认1，-1表示全速运行

from sklearn import linear_model
reg=linear_model.LinearRegression(fit_intercept=True,normalize=True)

然后就是训练数据，为方便可视化，我们可以用单变量关系的线性回归来验证

from sklearn import linear_model
import matplotlib.pyplot as plt#用于作图
import numpy as np#用于创建向量
reg=linear_model.LinearRegression(fit_intercept=True,normalize=False)
x=[[1],[4],[5],[7],[8]]
y=[1.002,4.1,4.96,6.78,8.2]
reg.fit(x,y)
k=reg.coef_   #获取斜率w1,w2,w3,...,wn
b=reg.intercept_  #获取截距w0
x0=np.arange(0,10,0.2)
y0=k*x0+b
plt.scatter(x,y)
plt.plot(x0,y0)

得到的结果如上图所示。如果想要多变量线性关系，只需要将对应一维的x数据改一下即可，例如：
from sklearn import linear_model
reg=linear_model.LinearRegression(fit_intercept=True,normalize=False)
x=[[1,3],[4,2],[5,1],[7,4],[8,9]]
y=[1.002,4.1,4.96,6.78,8.2]
reg.fit(x,y)
k=reg.coef_  #获取斜率w1,w2,w3,...,wn
b=reg.intercept_  #获取截距w0

此时输入变量为二变量，输出为单变量，得到的系数k和b如下：

k = array([0.97588271, 0.03692946])
b = -0.011345504840941878

参考文献：
https://zhuanlan.zhihu.com/p/24825503
https://zhuanlan.zhihu.com/p/38853908
《机器学习》（西瓜书）
《Hands-on Machine Learning with Scikit-Learn & Tensorflow》
2014年吴恩达机器学习课程
https://blog.csdn.net/u013709270/article/details/78667531
https://zhuanlan.zhihu.com/p/37588590
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression
https://blog.csdn.net/weixin_40930842/article/details/88882063