leecode 75-2 python 字符串的最大公因子

本人新手一枚，希望大佬们及时指导我的错误，万分感谢。

题目地址

LeetCode 75 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

对于字符串 s 和 t，只有在 s = t + t + t + ... + t + t（t 自身连接 1 次或多次）时，我们才认定 “t 能除尽 s”。

给定两个字符串 str1 和 str2 。返回 最长字符串 x，要求满足 x 能除尽 str1 且 x 能除尽 str2 。

示例 1：

输入：str1 = "ABCABC", str2 = "ABC"
输出："ABC"

示例 2：

输入：str1 = "ABABAB", str2 = "ABAB"
输出："AB"

示例 3：

输入：str1 = "LEET", str2 = "CODE"
输出：""

【1】暴力求解涌上心头，将短的那个字符串拿出来（我设为d），从长到短遍历这个d，比如d为abc，那么我们会判断abc->ab->a，哪个是最大公因子。为啥我从长到短遍历呢，因为题目问的返回最长字符串，要是问最短，那就从小到大遍历，你细品~

step1：找到那个比较短的字符串长度。

step2：从大到小遍历这个短字符串（其实在这里，遍历长的也行，如果它们真是有最大公因子，那么短的那个一定是长的那个的前缀）

step3：判断当前的字符串长度是否能被两个字符串长度整除同时还要满足str1=n个最大公因子，str2=m个最大公因子

代码：

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        #step1
        l1, l2 = len(str1), len(str2)
        lmin = min(l1, l2)
        #step2
        for i in range(lmin,0,-1):
            #step3
            if (l1%i)==0 and (l2%i)==0 and str1[:i]*(l1//i)==str1 and str1[:i]*(l2//i)==str2:
                return str1[:i]
        return ''

【2】看了官方的暴力算法，和我写的差不多，但是看了暴力算法的优化，我人麻了。又是一个不会的函数：

math.gcd(int1, int2)

这个函数是求最大公约数的，这时就想到了最小公倍数。最小公倍数当然可以通过最大公约数求解，math库也包含了相对应的方法：

#通过gcd求解
(x*y)/math.gcd(x, y)
#通过math库自带函数求解
math.lcm(x, y)

不得不说，得把math库里的基本运算方法得瞅瞅。看了一个手撸gcd的代码：

def gcd(a, b):
    while b:
        tmp = a
        a = b
        b = tmp % b
    return a

言归正传，开始步骤：

step1：找到两个数组长度最大公约数。

step2：看看这个最大公约数是不是可以满足str1=n个最大公因子，str2=m个最大公因子。（相比上一个方法，这个不用遍历了，时间复杂度下降）

代码：

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        #step1
        l1, l2 = len(str1), len(str2)
        l_gcd = math.gcd(l1,l2)
        #step2
        if str1[:l_gcd]*(l1//l_gcd)==str1 and str1[:l_gcd]*(l2//l_gcd)==str2:
            return str1[:l_gcd]
        else:
            return ''

【3】数学方法

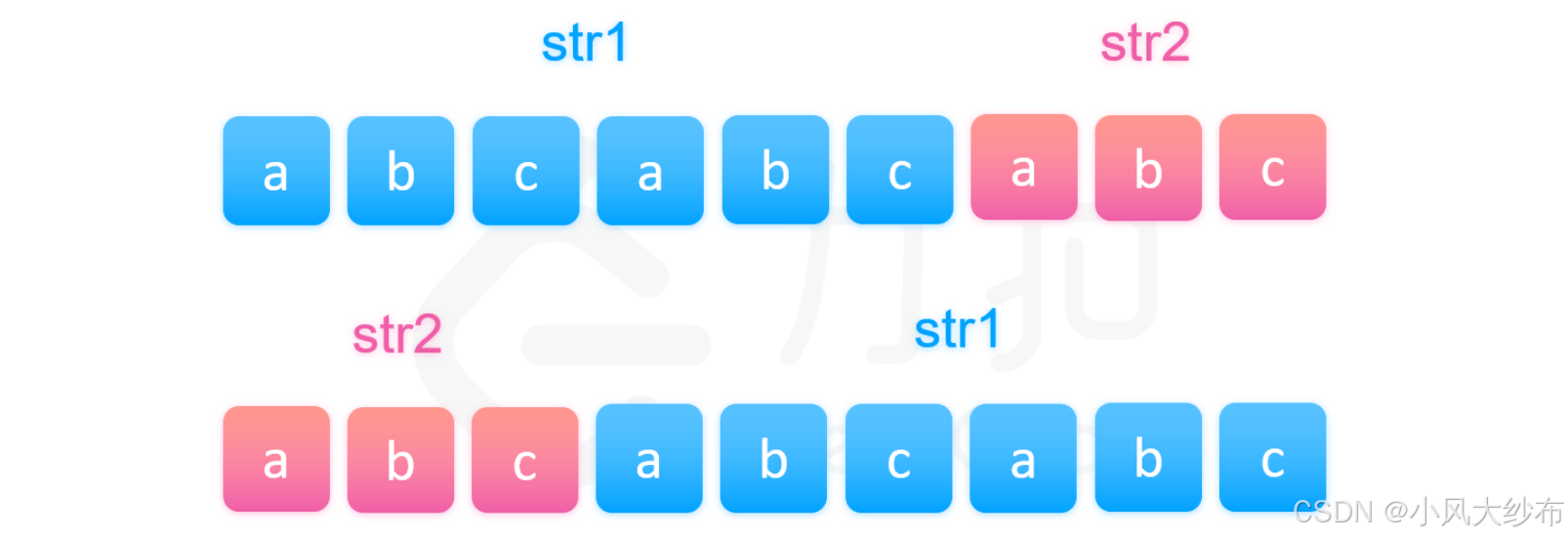
官方给了这样一个数学结论，str1+str2 = str2+str1，那么就存在最大公约数，所以这个只需要一步到位：

代码：

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        if str1+str2 == str2+str1:
            return str1[:math.gcd(len(str1),len(str2))]
        return ''

介个是真神奇！！！我记住它了！

欢迎大家批评指正。