不等式
- 基本不等式拓展: 2 a b a + b ≤ a b ≤ a + b 2 ≤ a 2 + b 2 2 ( 当且仅当 a = b 时取“ = ”号 ) \frac{{2ab}}{{a+b}} \le \sqrt{{ab}} \le \frac{{a+b}}{{2}} \le \sqrt{{\frac{{a\mathop{{}}\nolimits^{{2}}+b\mathop{{}}\nolimits^{{2}}}}{{2}}}} \left( \text{当}\text{且}\text{仅}\text{当}a=b\text{时}\text{取}\text{“}=\text{”}\text{号} \right) a+b2ab≤ab≤2a+b≤2a2+b2(当且仅当a=b时取“=”号)
- 均值不等式:
H
n
=
n
∑
i
=
1
n
1
x
i
=
n
1
x
1
+
1
x
2
+
⋯
+
1
x
n
(
调
和
平
均
数
)
G
n
=
∏
i
=
1
n
x
i
n
=
x
1
x
2
⋯
x
n
n
(
几
何
平
均
数
)
A
n
=
1
n
∑
i
=
1
n
x
i
=
x
1
+
x
2
+
⋯
+
x
n
n
(
算
术
平
均
数
)
Q
n
=
∑
i
=
1
n
x
i
2
=
x
1
2
+
x
2
2
+
⋯
+
x
n
2
n
(
平
方
平
均
数
)
H
n
≤
G
n
≤
A
n
≤
Q
n
H_{n}=\frac{n}{\sum \limits_{i=1}^{n}\frac{1}{x_{i}}}= \frac{n}{\frac{1}{x_{1}}+ \frac{1}{x_{2}}+ \cdots + \frac{1}{x_{n}}}(调和平均数)\\ G_{n}=\sqrt[n]{\prod \limits_{i=1}^{n}x_{i}}= \sqrt[n]{x_{1}x_{2}\cdots x_{n}}(几何平均数)\\ A_{n}=\frac{1}{n}\sum \limits_{i=1}^{n}x_{i}=\frac{x_{1}+ x_{2}+ \cdots + x_{n}}{n}(算术平均数)\\ Q_{n}=\sqrt{\sum \limits_{i=1}^{n}x_{i}^{2}}= \sqrt{\frac{x_{1}^{2}+ x_{2}^{2}+ \cdots + x_{n}^{2}}{n}}(平方平均数)\\ \\ H_{n}\leq G_{n}\leq A_{n}\leq Q_{n}
Hn=i=1∑nxi1n=x11+x21+⋯+xn1n(调和平均数)Gn=ni=1∏nxi=nx1x2⋯xn(几何平均数)An=n1i=1∑nxi=nx1+x2+⋯+xn(算术平均数)Qn=i=1∑nxi2=nx12+x22+⋯+xn2(平方平均数)Hn≤Gn≤An≤Qn
参考调和平均数-几何平均数-算术平均数-平方平均数的4种经典证明 - 柯西不等式: ( ∑ k = 1 n a k b k ) 2 ≤ ( ∑ k = 1 n a k 2 ) ( ∑ k = 1 n b k 2 ) \left( \sum_{k=1}^n a_k b_k \right)^{\!\!2}\leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right) (k=1∑nakbk)2≤(k=1∑nak2)(k=1∑nbk2)
- 绝对值不等式: ∣ a ∣ − ∣ b ∣ ≤ ∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣ \left| a \left| - \left| b \left| \le \left| a+b \left| \le \left| a \left| + \left| b \right| \right. \right. \right. \right. \right. \right. \right. \right. ∣a∣−∣b∣≤∣a+b∣≤∣a∣+∣b∣
- 排序不等式:设
a
1
≤
a
2
≤
⋯
≤
a
n
a_1\leq a_2 \leq \cdots \leq a_n
a1≤a2≤⋯≤an和
b
1
≤
b
2
≤
⋯
≤
b
n
b_1\leq b_2 \leq \cdots \leq b_n
b1≤b2≤⋯≤bn,
c
1
,
c
2
⋯
c
n
c_1,c_2 \cdots c_n
c1,c2⋯cn为b的任意序列,则有:
a
1
b
n
+
⋯
+
a
n
b
1
≤
a
1
c
1
+
⋯
+
a
n
c
n
≤
a
1
b
1
+
⋯
+
a
n
b
n
a_1b_n+\cdots +a_nb_1 \leq a_1c_1+\cdots +a_nc_n \leq a_1b_1+\cdots + a_nb_n
a1bn+⋯+anb1≤a1c1+⋯+ancn≤a1b1+⋯+anbn
即逆序和 ≤ \leq ≤乱序和 ≤ \leq ≤正序和 - 伯努利不等式 :
若 a > 0 , n > 1 , 则有 \text{若}a > 0,n > 1,\text{则}\text{有} 若a>0,n>1,则有
a n > 1 + n ( a − 1 ) (1) \mathop{{a}}\nolimits^{{n}} > 1+n{ \left( {a-1} \right) } \tag {1} an>1+n(a−1)(1)
当 a = b 1 n , b > 1 时,有 \text{当}a=\mathop{{b}}\nolimits^{{\frac{{1}}{{n}}}},b > 1\text{时}\text{,}\text{有} 当a=bn1,b>1时,有
b 1 n − 1 < b − 1 n (2) {\mathop{{b}}\nolimits^{{\frac{{1}}{{n}}}}-1 < \frac{{b-1}}{{n}}} \tag{2} bn1−1<nb−1(2)
级数
- 欧拉公式:
e
i
θ
=
cos
θ
+
i
sin
θ
e^{i\theta }=\cos \theta + i \sin \theta
eiθ=cosθ+isinθ
特别的当 θ = π 时 : \theta = \pi 时: θ=π时: e i π + 1 = 0 e^{i\pi} + 1=0 eiπ+1=0
证明:
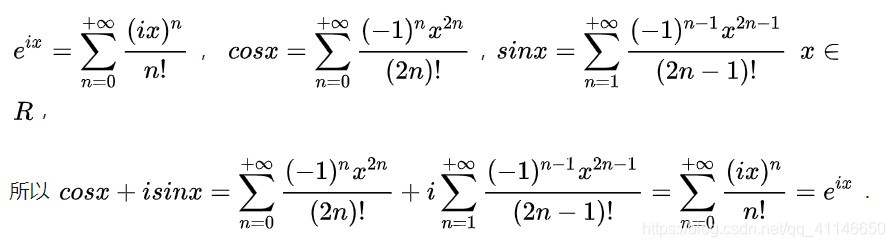
级数
-
f
(
x
)
,
g
(
x
)
在
[
a
,
b
]
f(x),g(x)在[a,b]
f(x),g(x)在[a,b]连续:
[
∫
a
b
f
(
x
)
g
(
x
)
d
x
]
2
⩽
∫
a
b
f
2
(
x
)
d
x
∫
a
b
g
2
(
x
)
d
x
\left[\int_{a}^{b} f(x) g(x) \mathrm{d} x\right]^{2} \leqslant \int_{a}^{b} f^{2}(x) \mathrm{d} x \int_{a}^{b} g^{2}(x) \mathrm{d} x
[∫abf(x)g(x)dx]2⩽∫abf2(x)dx∫abg2(x)dx
证明:若 f ( x ) ≡ 0 f(x)\equiv 0 f(x)≡0 显然成立
若 f ( x ) ≢ 0 f(x)\not\equiv 0 f(x)≡0 则 ∫ a b f 2 ( x ) d x > 0 \int_{a}^{b}f^2(x)dx>0 ∫abf2(x)dx>0,令 φ ( t ) = ∫ a b [ t f ( x ) + g ( x ) ] 2 d x = t 2 ∫ a b f 2 ( x ) d x + 2 t ∫ a b f ( x ) g ( x ) d x + ∫ a b g 2 ( x ) d x \varphi(t)=\int_{a}^{b}[t f(x)+g(x)]^{2} \mathrm{d} x=t^{2} \int_{a}^{b} f^{2}(x) \mathrm{d} x+2 t \int_{a}^{b} f(x) g(x) \mathrm{d} x+\int_{a}^{b} g^{2}(x) \mathrm{d} x φ(t)=∫ab[tf(x)+g(x)]2dx=t2∫abf2(x)dx+2t∫abf(x)g(x)dx+∫abg2(x)dx
则 φ ( t ) \varphi(t) φ(t)为二次多项式,在R上满足 φ ( t ) ⩾ 0 \varphi(t) \geqslant 0 φ(t)⩾0则 Δ = b 2 − 4 a c = [ 2 ∫ a b f ( x ) g ( x ) d x ] 2 − 4 ∫ a b f 2 ( x ) d x ∫ a b g 2 ( x ) d x ⩽ 0 \Delta =\mathop{{b}}\nolimits^{{2}}-4ac=\left[2\int_{a}^{b} f(x) g(x) \mathrm{d} x\right]^{2} -4 \int_{a}^{b} f^{2}(x) \mathrm{d} x \int_{a}^{b} g^{2}(x) \mathrm{d} x\leqslant 0 Δ=b2−4ac=[2∫abf(x)g(x)dx]2−4∫abf2(x)dx∫abg2(x)dx⩽0 - 若 ∫ a b f ( x ) d x = 1 \int_{a}^{b}f(x)dx=1 ∫abf(x)dx=1则有: [ ∫ a l x f ( x ) d x ] 2 = [ ∫ a b x f ( x ) ⋅ f ( x ) d x ] 2 ⩽ ∫ a b x 2 f ( x ) d x ⋅ ∫ a b f ( x ) d x = ∫ a b x 2 f ( x ) d x \left[\int_{a}^{l} x f(x) \mathrm{d} x\right]^{2}=\left[\int_{a}^{b} x \sqrt{f(x)} \cdot \sqrt{f(x)} \mathrm{d} x\right]^{2} \leqslant \int_{a}^{b} x^{2} f(x) \mathrm{d} x \cdot \int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} x^{2} f(x) \mathrm{d} x [∫alxf(x)dx]2=[∫abxf(x)⋅f(x)dx]2⩽∫abx2f(x)dx⋅∫abf(x)dx=∫abx2f(x)dx
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








