附录:所有blog的链接
数据结构学习笔记(1):基本概念
数据结构学习笔记(2):线性结构
数据结构学习笔记(3-5):树
数据结构学习笔记(6-8):图
数据结构学习笔记(9-10):排序
数据结构学习笔记(11):散列查找
数据结构学习笔记(12):综合习题选讲
第六讲 图(上)
6.1 什么是图
定义:
表示多对多的关系
包含
一组顶点:通常用 V V V(Vertex)表示顶点集合
一组边:通常用 E E E(Edge)表示边的集合
无向边是顶点对:
(
v
,
w
)
∈
E
(v,w)\in E
(v,w)∈E,其中
v
,
w
∈
V
v,w\in V
v,w∈V
有向边
<
v
,
w
>
<v,w>
<v,w>表示从
v
v
v指向
w
w
w的边(单行线)O-W
默认不考虑重边(无向边顶点相同的两条)和自回路(定点重点均是自己)
抽象数据类型定义
类型名称:图(Graph)
数据对象集: G ( V , E ) G(V,E) G(V,E)由一个非空的有限顶点集合 V V V和一个有限边集合 E E E组成(必须要由顶点)。
操作集:对于任意图 G ∈ G r a p h G \in Graph G∈Graph,以及 v ∈ V v\in V v∈V, e ∈ E e \in E e∈E
- Graph Create():建立并返回空图;
- Graph InsertVertex(Graph G,Vertex v):将v插入G;
- Graph InsertEdge(Graph G,Edge e):将e插入G;
- void DFS(Graph G,Vertex v):从顶点v出发深度优先遍历图G;
- void BFS(Graph G,Vertex v):从顶点v出发宽度优先遍历图G;
- void Shortestpath(Graph G,Vertex v,int Dist[]):计算图G中顶点v到任意其他顶点的最短距离;
- void MST(Graph G):计算图c的最小生成树;
- …
常见术语
有向图、无向图、网络(带权重的图)

图的表示
邻接矩阵表示法
没有自回路=>所以对角线是0
对于无向图有一半的空间被浪费=>右上角的左下角,被表示了两遍

备注:网络中有权重没有边相连的时候是否可以用0表示权重需要具体考量
优势:
直观、简单、好理解
方便检查任意一对顶点间是否存在边
方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
- 无向图:对应行(或列)非0元素的个数
- 有向图:对应行非0元素的个数是“出度”;对应列非0元素的个数是“入度”
劣势:
浪费空间—存稀疏图(点很多而边很少)有大量无效元素对稠密图(特别是完全图)还是很合算的
浪费时间—统计稀疏图中一共有多少条边很消耗时间
邻接表表示法
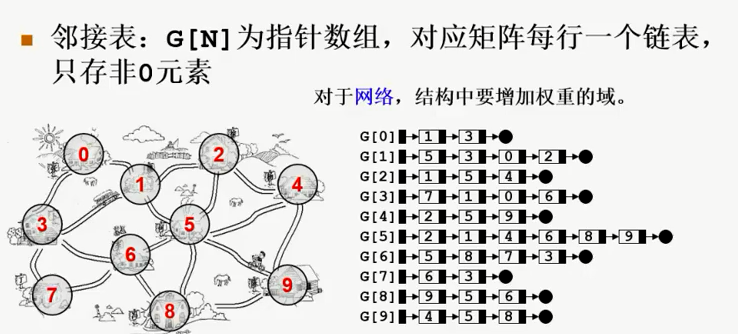
优势与劣势:
方便找任一顶点的所有“邻接点”
节约稀疏图的空间,需要N个头指针+2E个结点(每个结点至少2个域)
方便计算任一顶点的“度”?
- 对无向图:是的
- 对有向图:只能计算“出度”;需要构造“逆邻接表”(存指向自己的边)来方便计算“入度
方便检查任意一对顶点间是否存在边?No
6.2 图的遍历
全部访问一遍
深度优先搜索(Depth First Search,DFS)

广度优先搜索(Breadth First Search,BFS)

图不连通的情况解决
一些概念
连通: 如果从 V V V到 W W W存在一条(无向)路径,则称 v v v和 w w w是连通的
路径: V V V到 W W W的路径是一系列顶点 { V , v 1 , v 2 , … . v n , W } \{V,v_1,v_2,…. v_n,W\} {V,v1,v2,….vn,W}的集合,其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数(如果带权,则是所有边的权重和)。如果 V V V到 W W W之间的所有顶点都不同,则称简单路径。
回路: 起点等于终点的路径
连通图: 图中任意两顶点均连通
连通分量: 无向图的极大连通子图
- 极大顶点数:再加1个其他顶点就不符合连通的定义
- 极大边数:包含子图中所有顶点相连的所有边
强连通: 有向图中顶点 V V V和 W W W之间存在双向路径,则称 V V V和 W W W是强连通的
强连通图: 有向图中任意两顶点均强连通
强连通分量: 有向图的极大强连通子图
ABC均有两条路径 加上D就没有了
不连通图的遍历伪代码

6.3 应用实例:拯救007
6.4 应用实例:六度空间
小白专场:如何建立图- C语言实现
第七讲 图(中)
树之习题选讲-Tree Traversals Again
树之习题选讲-Complete Binary Search Tree
树之习题选讲- Huffman Codes
7.1 最短路径问题
最短路径问题的抽象
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径口这条路径就是两点之间的最短路径(shortest Path)
第一个顶点为源点(Source)
最后一个顶点为终点(Destination)
问题分类
单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径
- (有向)无权图
- (有向)有权图
多源最短路径问题:求任意两顶点间的最短路径
无权图的单源最短路算法
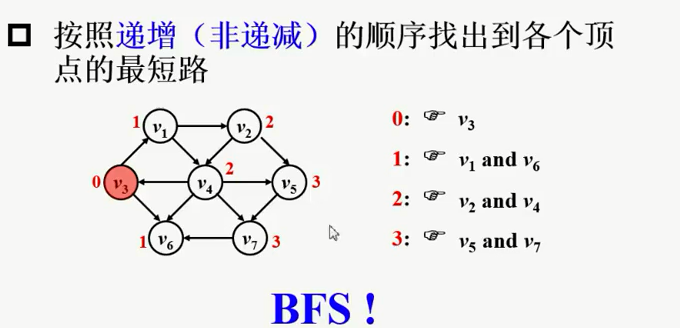

有权图的单源最短路算法
避免负值圈问题(一个回路不断地走收益可以无穷大)




多源最短路算法

方法一:单源执行多次
方法二:Floyd算法

算法思路:

小白专场:哈利·波特的考试- C语言实现
第八讲 图(下)
8.1 最小生成树问题
定义
是一棵树
无回路
∣ V ∣ |V| ∣V∣个顶点一定有 ∣ V ∣ − 1 |V|-1 ∣V∣−1条边
是生成树
包含全部顶点
∣ V ∣ − 1 |V|-1 ∣V∣−1条边都在图里
边的权重和最小,向生成树中加任何一条边都一定构成回路
最小生成树存在等价于图连通
算法:贪心算法
每一步都要最好的
权重最小的边
Prim算法

想法流程:
初始化一个最小生成树
一直循环直到所有的联通节点都被添加进最小生成树,跳出循环。跳出循环检查一下,如果还有点在外面那么说明有问题,是不连通图爆出错误。
循环内部:dist的初始化值与s相连的更新为权重,其他的没有直接相连的就是正无穷因为都暂时不连接,等待之后更新。
将最小距离的那个点收进来,设置它的距离为0,此时他已经在树里面了默认到树的距离是0。收录进新的v之后需要更新与v相连点的w到树的距离并更新他们的路径。这样之后会迭代的把所有点都纳入进树。

Kruskal算法一将森林合并成树

8.2 拓扑排序
AOV定义

拓扑序:
如果图中从 v v v到 w w w有一条有向路径,则 v v v一定排在 w w w之前。满足此条件的顶点序列称为一个拓扑序
拓扑排序
获得一个拓扑序的过程就是
AOV如果有合理的拓扑序,则必定是有向无环图(Directed Acyclic Graph,DAG)
拓扑排序的算法


AOE定义

关键路径问题









 本文深入探讨图论的基本概念,包括有向图、无向图及网络,并详细讲解图的表示方法如邻接矩阵与邻接表。此外,文章还介绍了图的遍历算法,如深度优先搜索和广度优先搜索,以及图的应用实例,例如最短路径问题和最小生成树问题的解决策略。
本文深入探讨图论的基本概念,包括有向图、无向图及网络,并详细讲解图的表示方法如邻接矩阵与邻接表。此外,文章还介绍了图的遍历算法,如深度优先搜索和广度优先搜索,以及图的应用实例,例如最短路径问题和最小生成树问题的解决策略。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








