洛谷—题解 P1101 单词方阵

原题链接P1101 单词方阵

有条件的小伙伴可以点进原网站开题，也可直接看我下面的截图



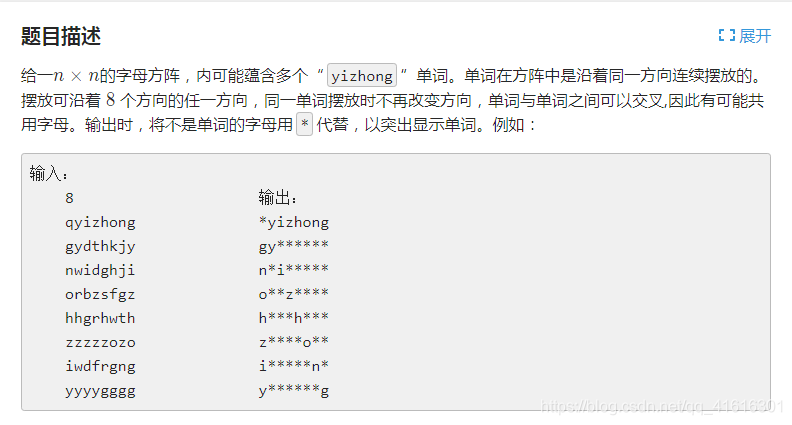
废话一堆
 艾瑞巴蒂，我可爱的小伙伴们！我也是很久没有写题解了，因为疫情的关系，在家我TM实在太闲了…做做题，写写没人看的题解，虽然帮不上别人什么，但写完自己确实灰常灰常开森。

题解
 这是一个相对有点难度的深度搜索(DFS)题目。
 Attention:比较和迷宫类问题不一样的是，此题的搜索方向是8个方向。难点如下：
 首先,确定搜索下一步的判定条件，即cur==6||word[dx][dy]==norm[cur+1]。这也几乎是所有搜索类型问题的一个小问题。满足条件就继续递归，否则结束。
 其次是，当完成每次递归时保存路径，标注这条可行的路径（方便后续输出答案）。
 注：输出答案时，各位小伙伴在格式上细心一点，博主已经在输出上翻车无数次了（不单单是这道题）。everybody，学会了嘛？

来人！上代码！

#include<iostream>
#include<cstdio>
#include<cstring>
#include<math.h>

using namespace std;

const int maxn = 101;

struct node
{
	int x,y;
};

struct node c[maxn]; //记录搜索路径 
char word[maxn][maxn]; //储存单词方阵 
char norm[] = "yizhong"; //标准串 
int vis[maxn][maxn]; //标签，确定每个点是不是结果 
int dir[][2] = {{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
//上下左右，左上，左下，右上，右下，八个方向 

void dfs(int x, int y, node c[],int k, int cur)
{
	if(cur==7){
		for(int i=0;i<7;i++)
		vis[c[i].x][c[i].y]=1;
	}
	else{
		int dx=x+dir[k][0]; //调整方向 
		int dy=y+dir[k][1];
		if(cur==6||word[dx][dy]==norm[cur+1]){
			c[cur].x=x;
			c[cur].y=y;
			dfs(dx,dy,c,k,cur+1);
		}
	}
}

int main()
{ 
	int n;
	scanf("%d",&n);
	for(int i=0;i<n;i++)
		scanf("%s",word[i]);
		
	memset(vis,0,sizeof(vis)); //数组置零 
	
	//深搜开始 
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(word[i][j]=='y'){
				for(int k=0;k<8;k++){
					int x=i+dir[k][0];
					int y=j+dir[k][1];
					if(word[x][y]=='i')
						dfs(i,j,c,k,0);
				}
			}			
		}
	}

	//输出答案 
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(vis[i][j]) printf("%c",word[i][j]);
			else printf("*");
		}
		printf("\n");
	}
	return 0;
 } 

祝福各位小伙伴们学的开心，学的快乐，早早的成为大牛。
曲终未必人散，有缘自会相逢
我是Mario，一个立志要考进MIT的程序猿。

[^注]：以上内容仅是个人观点，如涉及版权等问题，请联系我第一时间内删除。