1⃣️范数

范数>=0
- ||A||∞:行和范数,计算方式:{一行中每个元素的绝对值之和}max,本题答案是:|-i|+|2|+|5|=8
- ||A||1:列和范数,计算方式:{一列中每个元素的绝对值之和}max,本题答案是:|i|+|2|+|5|=8
- ||A||F:F-范数,计算方式:矩阵元素绝对值的平方之和在开根号,本题答案是:sqrt(|1|2+|0|2+|i|2+|0|2+|1|2+|2|2+|-i|2+|2|2+|5|2)=sqrt(37)
- ||A||2:2-范数,计算方式:sqrt({ATA矩阵特征值的绝对值}max)
- ||A||m∞:计算方式:n*{矩阵元素绝对值}max ,其中n为列数
- ||A||m1:计算方式:矩阵元素绝对值之和
**补充:向量的范数**
- ||x||∞:计算方式:元素的绝对值的最大值
- ||A||-∞:计算方式:元素绝对值的最小值
- ||A||1:计算方式:列绝对值和
- ||A||2:计算方式:sqrt(列的绝对值的平方和)
- ||A||P:计算方式:pow(列的绝对值的平方和,1/P),其中pow(a,1/p)为对a开p次方根
2⃣️Jordan标准型

Jordan标准型即每个特征值对应的小矩阵主对角线为特征值,主对角线上方对角线元素为1,其余部分为0
步骤:
1.计算特征多项式(即|λE-A|=(λ-λi)m)
2.解出的特征多项式如果是(λ-3)2(λ-1)形式,则为两个小Jordan 型拼接而成,如图:

如果解出的特征多项式是(λ-3)4形式,则求出的其jordan标准型,如图:
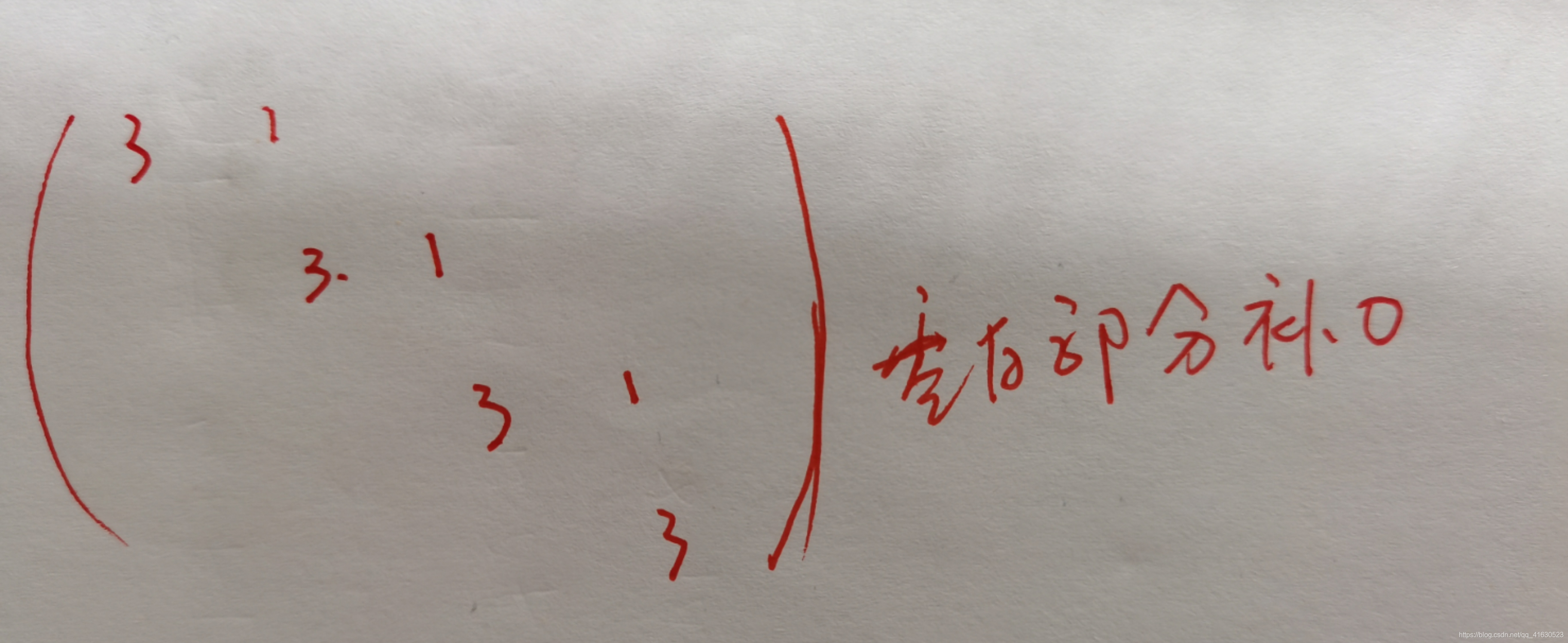
3⃣️判断一个矩阵是否为收敛矩阵

判断一个矩阵是否为收敛矩阵,常见做法是判断其谱半径<1,而谱半径={|特征值|}max。如果对矩阵求谱半径比较困难或者不是特别方便的时候,也可以选择对谱半径的范围进行估计,具体做法是,谱半径会<={行/列绝对值之和}max(其实就是谱半径<=||A||1或者||A||∞)
上题答案是:是收敛矩阵,理由是:谱半径<=||A||1=|1/4|+|1/2|=0.75<1
4⃣️判断矩阵(幂)级数是否收敛

判断一个矩阵(幂)级数是否收敛,常见做法是判断其谱半径<收敛半径(谱半径求法在上面第3点),而收敛半径=ak+1/ak(数列ak是指矩阵幂级数中Ak前面那一块,比如上题中ak=k(k+1),ak+1=(k+1)(k+2),上题收敛半径就为k/k+2=1)
上题答案是:谱半径<=||A||∞=0.9<1
5⃣️Householder矩阵

若A为Householder矩阵,则|A|=-1;若G为Givens矩阵,则|G|=1
6⃣️投影

正交投影矩阵计算方法:PL=L(LTL)-1LT
投影矩阵计算方法: PL,M=(L|0)(L|M)-1(其中0为0阵)
计算投影方法:投影矩阵*x
上题答案(1):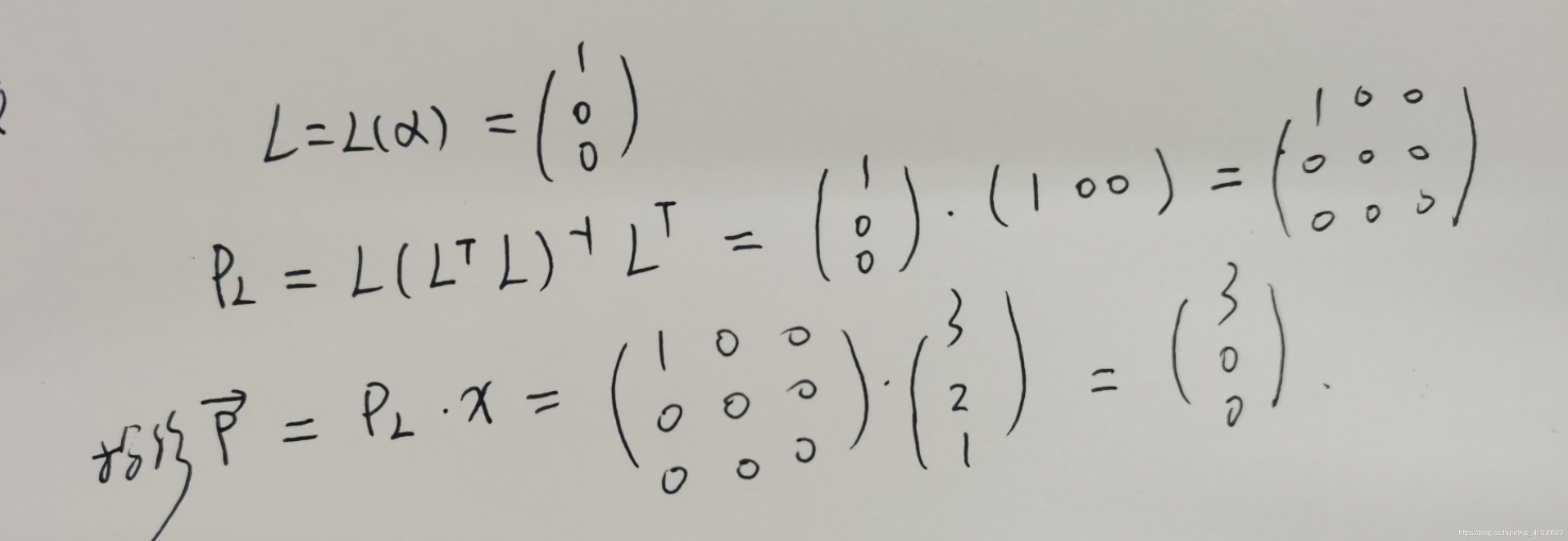
答案(2)
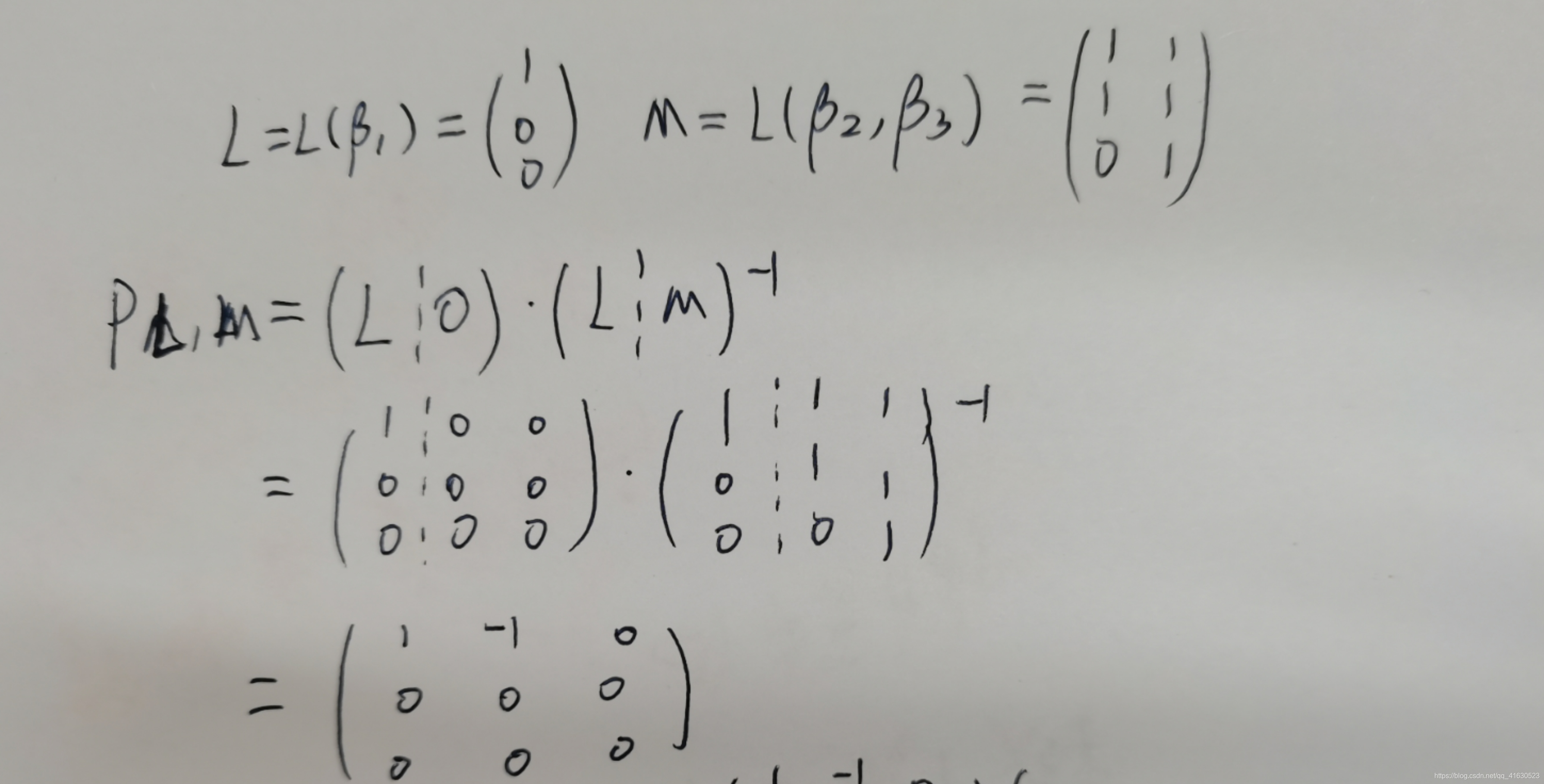
7⃣️酉不变范数
如果某范数满足||PAQ||=||A||,且P,Q为酉矩阵,则说这个范数具有酉不变性,F-范数和2-范数都是酉不变范数。
8⃣️求矩阵幂级数和
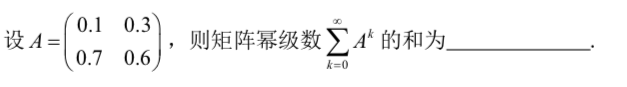
计算方法:矩阵A收敛,则矩阵幂级数和为(E-A)-1
9⃣️三角分解(LU分解)
将矩阵分解成下三角矩阵和上三角矩阵的乘积

步骤:(1)对矩阵A进行第三类初等行变换(即第i行的m倍加到第j行),使得A变成一个上三角矩阵U。
(2)对A左乘一系列单位下三角矩阵(L1,L2,…,Lk),使得L1L1…LkA=U
上题答案: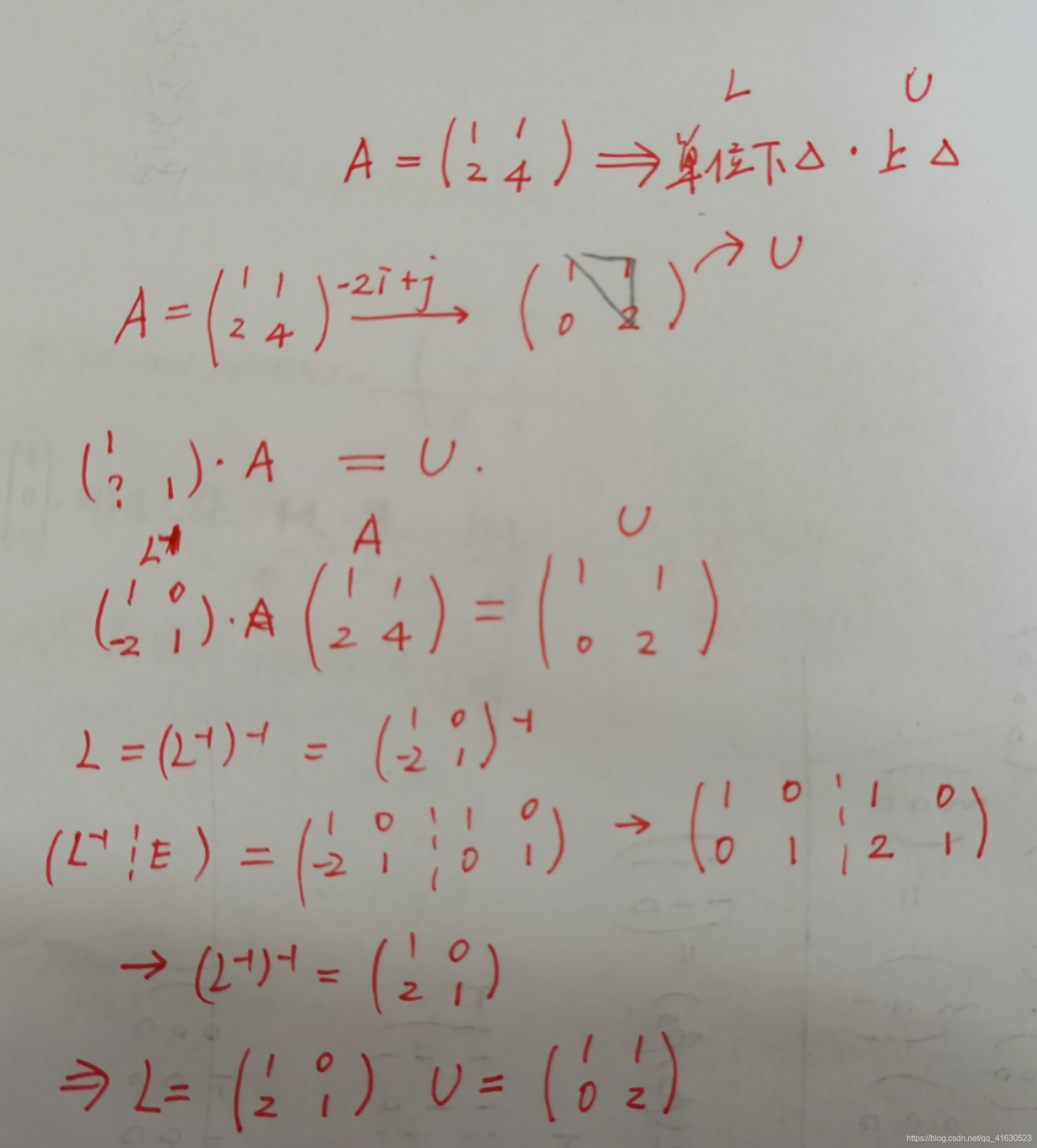
🔟直积
直积即笛卡尔积,具体计算方法是:A中的每一个元素aij*矩阵B
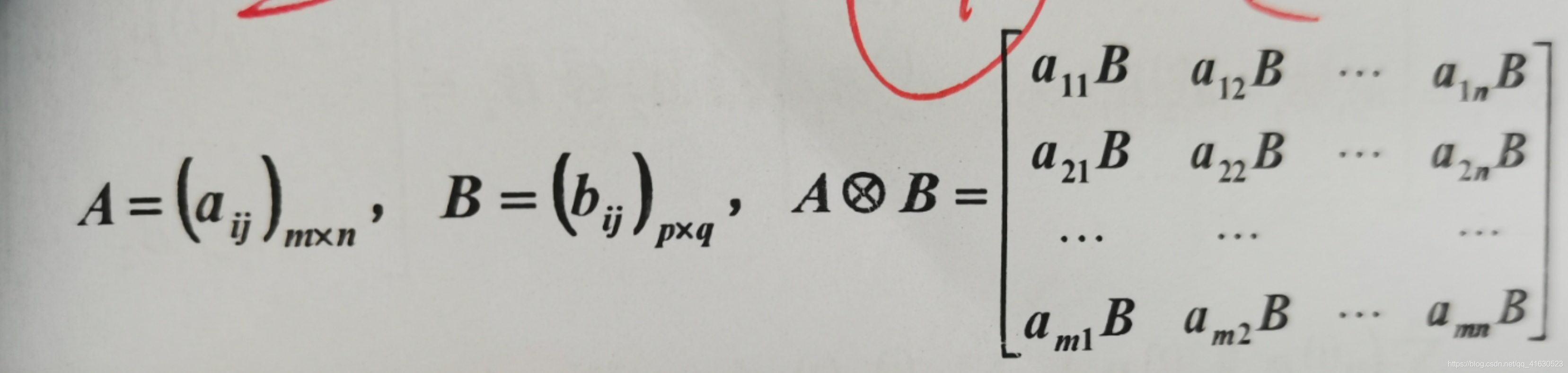























 1190
1190

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








