1553. 吃掉 N 个橘子的最少天数（记忆化+贪心优化）

本文链接：https://blog.csdn.net/qq_41661809/article/details/134571446

Problem: 1553. 吃掉 N 个橘子的最少天数

文章目录

题目
思路
Code

题目

使得 n 变成0的操作有三种方式：

吃掉一个橘子。
如果剩余橘子数 n 能被 2 整除，那么你可以吃掉 n/2 个橘子。
如果剩余橘子数 n 能被 3 整除，那么你可以吃掉 2*(n/3) 个橘子。

思路

如果我们每天吃一个橘子（每次是操作1），那么从n到0要经过n天，所以最坏的情况下就是n。要想保证天数最少，最好每天吃的最多。最暴力的方法就是

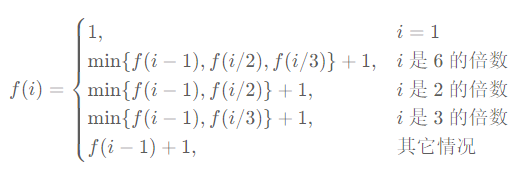
class Solution {
public:
    // 记录吃掉n 个橘子的最少天数
    unordered_map<int,int> memo ; 
    int minDays(int n) {
        if(n == 1 ) {
            memo[n] = 1 ; 
            return 1 ; 
        }
        if(memo.count(n)) {
            return memo[n] ; 
        }
        if(n%2 == 0 && n%3 ==0 ){
            memo[n] = min( minDays(n/2), minDays(n/3)) +1  ;
            memo[n] = min(memo[n] ,minDays(n-1)) ; 
            return memo[n] ; 
        }else if(n %2 == 0 && n%3 !=0 ){
            
            return memo[n] = min (minDays(n/2) , minDays(n-1) ) +1 ; ; 
        }else if( n%3 ==0 && n%2 !=0) {
             
            return memo[n] = min( minDays(n/3) , minDays(n-1) )+1  ; 
        }else{

            return memo[n] = minDays(n-1) +1 ;
        }
        return memo[n] ; 
    }
};

但是显然是导致栈溢出

优化一下

我们肯定是希望吃掉一个橘子这样的操作尽可能少（贪心）。优先选择操作2和3.

假设，我们对n 先进行k次操作，然后再进行操作2，那么橘子的数量就从n 变成了(n-k)/2 。一共操作了 k+1次；如果我们先将n变成靠近2的倍数的那个数 $n_{t} ( n_{t} < n$ )，然后再执行操作1. 假设 $k_{0}$ 是 $n- n_{t}|$ , $k_{0}$ 是模2的余数,那么我们只需要执行 $k_{0}$ 次的操作1(靠近2的倍数) ，然后执行1次操作2 和 $k-k_{0})$ 次的操作1，即eq.1
$\frac{(n-k_{0})}{2} -\frac{ (k-k_{0})}{2} = \frac{(n-k)}{2} （1）$
一共执行了 $k_{0} +1 + \frac{(k-k_{0})}{2}$ 次小于 $k + 1$ 次。
同理操作3 也是可以这样处理。

Code

class Solution {
public:
    unordered_map<int,int> memo; 
    int minDays(int n) {
        if(n <=1 ) return n ; 
        if(memo.count(n) ) {
            return memo[n] ; 
        }
        // 通过操作1减少到靠近2和3的倍数
        int k0_2 =  n%2 ; 
        int k0_3 =  n%3 ; 
        return memo[n] = min(k0_2 +minDays(n/2) , k0_3 +minDays(n/3) ) +1; 
    }

};