Polya定理

  在着色问题上常常用到Polya 定理来解决计数问题,是组合数学的基本定理之一 .

  首先先引入置换群 ,

             设 S = { 1,2,3...n} , S 上的任何双射函数  : S -> S 称为 S 上的 n 元置换 .

 可以表示成这样.

          设  是 S = {1,2,3 .... . n } 上的n元置换 . 若  (i1) = i2   , (i2) = i3  ,   (i3) = i4 .... ..  (i k-1) = i k ,  (ik ) = i1 ; 且 保持S中的其他元素不变 , 则称  为 S 上的 k 阶 轮换 , 记作 ( i1 , i2 .. ik ) , 若k  = 2 ,称为 为 S 上的对换. 

          设S = {1,2, . . n } , 对于任何 S 上的 n 元置换  一定存在着一个有限序列  i1 , i2 .... ik , k>=1 ,使得 , 

                             (i1) = i2   , (i2) = i3  ,   (i3) = i4 .... ..  (i k-1) = i k ,  (ik ) = i1 ; 

           令   = (i1, i2 .. .. ik) ,它是从  中分解出来的第一个轮换 .根据 函数的复合定义可以将  写作 1 '  ,其中 ' 作用于

S- {i1 , i2 , ...ik} , 而 S 有 n 个元素 ,因此可以继续 对 ' 继续进行 分解,经过有限次的分解后, 我们可以得到 

                                                        = 1 2 ...... t 

  不难看出在分解式中任何两个轮换 i 和 j  都是不相交的 , 所以 n 元 置换就可以表示成轮换之积 . 

比如 : 

             

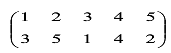
  这是一个  5 元 置换 ,  (1) = 3 , (3) = 1  ;     (2) = 5 , (5) = 2 ;         (4 ) = 4  ; 

  在上面这个置换中看到，1置换为3，同时3又能置换为1，这就是一个循环。4置换为4本身，这也算一个循环。所以上面的置换    可以写成这样：

                             = (1,3)(2,5)(4)  , 一般一阶轮换(4) 也可以省略不写 ,   = (1,3)(2,5) .

    Polya 定理 

        

设 N    = { 1,2, .... n } 是被着色物体的集合 , G = {1 , 2 ,  .... g} 是 N 上的置换群 . 用 m 种颜色对 N中的元素进行着色,则在G的作用下不同的着色方案数是:  

                                                  

其中 c( k) 是循环节数 ,  上面的例子中  1 = (1,3 )   ,2 = (2,5)  ,3 = (4)  ; 所以 c(1) = 2  , c(2) = 2  , c(3) = 1 ; 

 

比如使用 黑白两种颜色对 下面的方格进行染色 , 如果允许方格可以绕 中心点旋转, 问有多少种不同的着色方案数 ?

    

1	2
3	4

方格可以 旋转 0° , 90 ° , 180 ° ,270° . 所以 群G = {  0° , 90 ° , 180 ° ,270° } , G的阶|G| =  4  ,

G 中 所有的置换是      1 = (1)   ,2 = (1,2,3,4)  ,3 = (1,3)(2,4), 4 = (1,4,3,2) ; 

                                   c(1) = 4  , c(2) = 1  , c(3) = 2 , c( 4) = 1 

带入 Polya定理  M  =     .