Combined DWT-DCT Digital Image Watermarking Ali Al-Haj论文（含python代码）

代码链接
https://github.com/diptamath/DWT-DCT-Digital-Image-Watermarking.git

前言

这篇论文是在2007年发表的，有些时间了，但是作为数字水印发展较好的时代，通过 这篇文章可以学习DCT，DWT在数字水印技术的应用，

论文创新点

结合小波变换和离散余弦变换的数字图像水印
本文将描述一种基于两种变换相结合的数字图像水印算法；DWT和DCT。水印是通过改变仔细选择的小波变换子带的小波系数，然后在选择的子带上应用离散余弦变换来实现的。

DCT

离散余弦变换:离散余弦变换是一种将信号转换成基本频率分量的技术[9]。它将图像表示为不同幅度和频率的正弦曲线的总和。对于输入图像x，根据等式计算变换输出图像y的离散余弦变换系数。1如下所示。在等式中，x是具有N×M个像素的输入图像，x(m，N)是图像的行M和列N中的像素的强度，y(u，v)是离散余弦变换矩阵的行u和列v中的离散余弦变换系数。

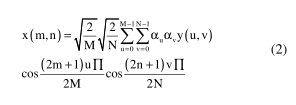
上图是x与y的关系。
这篇文章用到了基于块的离散余弦变换，现将原图分割成不重叠的块，然后对每个块做离散余弦变换，这导致给出三个频率子带:低频子带、中频子带和高频子带。

那怎么让图片的可见性不受影响呢？
刚刚我们说到图像可以分为三个频率子带:低频子带、中频子带和高频子带，大部分信号是位于位于低频子带，其中包含图像最重要的视觉部分。第二个，图像的高频成分通常通过压缩和噪声攻击来去除。因此，通过修改****中频子带的系数来嵌入水印，使得图像的可见性不会受到影响，并且水印不会通过压缩被移除

DWT

小波变换:小波是一种特殊的函数，其形式类似于傅立叶分析中的正弦和余弦，被用作表示信号的基本函数。对于二维图像，应用离散小波变换对应于通过二维滤波器在每个维度上处理图像。滤波器将输入图像分成四个不重叠的多分辨率子带LL1、LH1、HL1和HH1。子带LL1表示粗略尺度的小波变换系数，而子带LH1、HL1和HH1表示小波变换系数的精细尺度。为了获得下一个更粗尺度的小波系数，子带LL1被进一步处理，直到达到某个最终尺度N。当到达N时，我们将有3N+1个子带，由多分辨率子带LLN和LHx、HLx和HHx组成，其中x的范围从1到N

DWT 的优点

1、由于其良好的空间频率定位特性，小波变换非常适合于识别宿主图像中可以有效嵌入水印的区域
2、

分析代码

原图

img=Image.open('lena.jpg')
#将模式转变为L就是灰度图像
img = img.convert('L')
print(img)
Image._show(img)

getData

img=Image.open('lena.jpg')
print(img)
str=img.getdata()
print(str[1])
img = img.convert('L')

原图

水印图片

代码

range（）

for x in range(0, 7, 8):
    print(x)

for x in range(0, 16, 8):
    print(x)

for x in range(0, 17, 8):
    print(x)

np.empty()

all_subdct = np.empty((5, 5))
print(all_subdct)

可以看出默认类型是浮点类型numpy.float64

import numpy as np
import pywt
import os
from PIL import Image
import cv2
from scipy.fftpack import dct
from scipy.fftpack import idct

# img11=Image.open('F:\girl.jpg')
dir=os.getcwd()
image = 'lena.jpg'
watermark = 'boy.png'

# 返回灰度图片的uint值
def convert_image(image_name, size):
    # 将图片转为灰度图像
    img = Image.open(image_name).resize((size, size), 1)
    img = img.convert('L')
    # img.save('./dataset/' + image_name)
    image_array = np.array(img.getdata(), dtype=np.float).reshape((size, size))
    print (image_array[0][0])
    print (image_array[10][10])
    return image_array
# 多尺度小波变换
def process_coefficients(imArray, model, level):
    coeffs=pywt.wavedec2(data = imArray, wavelet = model, level = level)
    # print coeffs[0].__len__()
    coeffs_H=list(coeffs) 
   
    return coeffs_H


def embed_mod2(coeff_image, coeff_watermark, offset=0):
    for i in xrange(coeff_watermark.__len__()):
        for j in xrange(coeff_watermark[i].__len__()):
            coeff_image[i*2+offset][j*2+offset] = coeff_watermark[i][j]

    return coeff_image

def embed_mod4(coeff_image, coeff_watermark):
    for i in range(coeff_watermark.__len__()):
        for j in range(coeff_watermark[i].__len__()):
            coeff_image[i*4][j*4] = coeff_watermark[i][j]

    return coeff_image

            
    
def embed_watermark(watermark_array, orig_image):
    # 求得水印数组的大小
    watermark_array_size = len(watermark_array[0])
    #将多维数组降为一维数组
    watermark_flat = watermark_array.ravel()
    ind = 0

    for x in range (0, orig_image.__len__(), 8):
        for y in range (0, orig_image.__len__(), 8):
            if ind < watermark_flat.__len__():
                subdct = orig_image[x:x+8, y:y+8]
                subdct[5][5] = watermark_flat[ind]
                orig_image[x:x+8, y:y+8] = subdct
                ind += 1 


    return orig_image
      


def apply_dct(image_array):
    size = image_array[0].__len__()
    all_subdct = np.empty((size, size))
    for i in range (0, size, 8):
        for j in range (0, size, 8):
            subpixels = image_array[i:i+8, j:j+8]
            subdct = dct(dct(subpixels.T, norm="ortho").T, norm="ortho")
            all_subdct[i:i+8, j:j+8] = subdct

    return all_subdct


def inverse_dct(all_subdct):
    size = all_subdct[0].__len__()
    all_subidct = np.empty((size, size))
    for i in range (0, size, 8):
        for j in range (0, size, 8):
            subidct = idct(idct(all_subdct[i:i+8, j:j+8].T, norm="ortho").T, norm="ortho")
            all_subidct[i:i+8, j:j+8] = subidct

    return all_subidct


def get_watermark(dct_watermarked_coeff, watermark_size):
    
    subwatermarks = []

    for x in range (0, dct_watermarked_coeff.__len__(), 8):
        for y in range (0, dct_watermarked_coeff.__len__(), 8):
            coeff_slice = dct_watermarked_coeff[x:x+8, y:y+8]
            subwatermarks.append(coeff_slice[5][5])

    watermark = np.array(subwatermarks).reshape(watermark_size, watermark_size)

    return watermark


def recover_watermark(image_array, model='haar', level = 1):


    coeffs_watermarked_image = process_coefficients(image_array, model, level=level)
    dct_watermarked_coeff = apply_dct(coeffs_watermarked_image[0])
    
    watermark_array = get_watermark(dct_watermarked_coeff, 128)

    watermark_array =  np.uint8(watermark_array)

#Save result
    img = Image.fromarray(watermark_array)
    img.save('./result/recovered_watermark.jpg')


def print_image_from_array(image_array, name):
  
    image_array_copy = image_array.clip(0, 255)
    image_array_copy = image_array_copy.astype("uint8")
    img = Image.fromarray(image_array_copy)
    img.save('./result/' + name)



def w2d(image,watermark):
    model = 'haar'
    level = 1
    image_array = convert_image(image, 2048)
    watermark_array = convert_image(watermark, 128)

    coeffs_image = process_coefficients(image_array, model, level=level)
    dct_array = apply_dct(coeffs_image[0])
    dct_array = embed_watermark(watermark_array, dct_array)
    coeffs_image[0] = inverse_dct(dct_array)
  

# reconstruction
    image_array_H=pywt.waverec2(coeffs_image, model)
    print_image_from_array(image_array_H, 'image_with_watermark.jpg')



# recover images
    recover_watermark(image_array = image_array_H, model=model, level = level)




w2d(image,watermark)

# [LL1,(LH1,HL1,HH1)]=process_coefficients(original_image,'haar',1)
# [LL2,(LH2,HL2,HH2)]=process_coefficients(HL1,'haar',1)
# HL2=embed_mod4(HL2,watermark)
# apply_dct(HL2)

运行结果

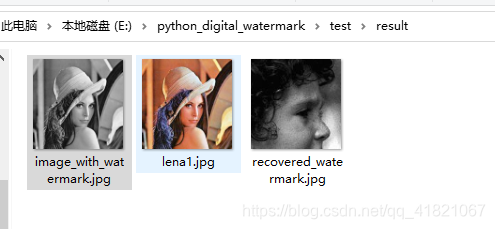
代码解析

步骤

第一步:应用DWT将覆盖宿主图像分解为四个不重叠的多分辨率子带:LL1、HL1、LH1和HH1。

image_array = convert_image(image, 2048)
watermark_array = convert_image(watermark, 128)
coeffs_image = process_coefficients(image_array, model, level=level)

第二步:再次对子带HL1应用DWT，得到四个更小的子带，选择HL2子带，如图2 a所示。或者，对子带HH1应用DWT，得到四个更小的子带，选择HH2子带，如图2 b所示。

第三步:将子带HL2(或HH2)分成4×4块。
第四步:对所选子带(HL2或HH2)中的每个块应用离散余弦变换。
第五步:将灰度级水印图像重新公式化为0和1的向量。
第六步:生成两个不相关的伪随机序列。一个序列用于嵌入水印位0 (PN_0)，另一个序列用于嵌入水印位1 (PN_1)。两个伪随机序列中每一个的元素数量必须等于经离散余弦变换的离散小波变换子带的中带元素数量。第七步:将PN_0和PN_1两个伪随机序列嵌入一个增益因子？在宿主图像的所选离散小波变换子带的离散余弦变换4×4块中。

提取水印

不需要原始图像，是盲水印，
第一步:应用小波变换将水印图像分解为四个不重叠的多分辨率子带:LL1、HL1、LH1和HH1。

第二步:对HL1应用DWT得到四个更小的子带，选择子带HL2，如图2 a所示，或者对HH1子带应用DWT得到四个更小的子带，选择HH2子带，如图2 b所示

第三步:将子带HL2(或HH2)分成4×4块。

第四步:对所选子带(HL2或HH2)中的每个块应用离散余弦变换，并提取每个离散余弦变换块的中带系数。
代码中第三步和第四步合在一起
第五步:使用水印嵌入过程中使用的相同种子，重新生成两个伪随机序列(PN_0和PN_1)。

第六步:对于子带HL2(或HH2)中的每个块，计算中间带系数和两个生成的伪随机序列(PN_0和PN_1)之间的相关性。如果与PN_0的相关性高于与PN_1的相关性，则提取的水印比特被认为是0，否则提取的水印被认为是0