机器学习模型（线性回归、逻辑回归、决策树和随机森林、SVM&向量机）

R/python/jupter
jupter notebook

包

mpl_finance

数据清洗与特征选择
OpenCV图像处理
时间序列分析
疫情模拟
机器学习与深度学习

机器学习模型

股价预测

方法：自回归

loss

SGD

线性回归（模型是什么样？损失函数是什么？）、逻辑回归

高斯分布，最大似然估计MIE，最小二乘法
逻辑回归和softmax和神经网络中的全连接层

houseing.data

500多个不同房屋的信息
m=506,n=13,Xmn Ym1
(xi,yi)
输入xi,输出yi,
xi---->yi得到一个模型。
yi=Model(xi，Θ)
参数记为Θ，里面含有多个参数，Θ是个向量，x,y是已知，
Θ是未知向量，VGGNet :138M 参数， 线性回归：14个
yi_predice与yi之间误差总和（平方和）是最小的。（yi_predice（Θ）-yi）（2）
CROSS Entropy：交叉熵
SSE
MSE：均方误差，
loss=模型误差和/个数m,loss只与Θ有关，称为损失函数。
Θ初始化：随机/先验
我们不知道函数是什么？对损失函数求偏导。∂loss/∂θ,沿着负梯度做下降？Θ

技术点
梯度下降算法
最大似然估计

线性回归

模型是什么？
一元，二元，

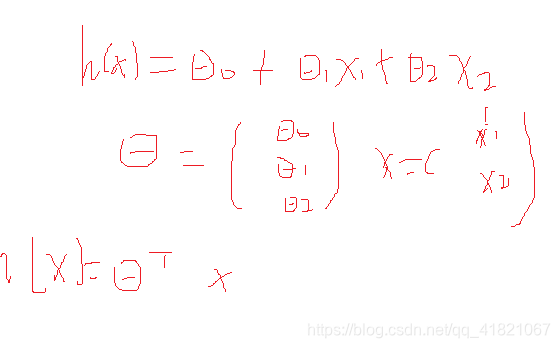
损失函数是什么

误差有正有负

去猜服从什么分布！

高斯是不直观，欧拉是直观，自己去确定的。
（假设）误差是独立同分布的，服从均值为0，方差为σ²的高斯分布、
P(y1,y2,y3…ym)是似然概率。
L(Θ)最大似然函数。

图上的x,y是训练样本
使用梯度下降算法不能保证是最优的。

防止过拟合

y值可以通过X的值求出来。
可以求得Θ是9行一列的，就是从（a0…a8）