动态规划(DP)理论

上一篇专栏主要用几个程序来解释了回溯和动态规划之前的区别，但是没有说出动态规划本质的特色，就像贪心算法的三个步骤一样，直抒胸臆，于是这篇专栏便会主要围绕着解题思路来讲，目的就是让大家明白什么样的问题可以使用动态规划算法，解决动态规划问题的思路是什么样的，贪心，分治，回溯，动态规划这四种算法的思想又有什么区别和联系？

首先来说一下什么样的题目适合采用dp思想

一个模型三个特征

首先我们来看一下什么是一个模型？指的是动态规划更习惯性的解决问题的模型，我们将这个模型初步定义为“多阶段决策最优解模型”

因为呢，我们一般采用dp算法获取最优解的过程中，需要有很多个决策，每一个决策对应一种状态，保证全局最优，获取最优解。

然后来说一下三个特征，它们分别是最优子结构，无后效性和重复子问题。下面来一一介绍一下。

1. 最优子结构

指的是，我们可以通过子问题的最优解，逆推到大问题的最优解，而如果我们能把这个子结构对应到我们实际问题的模型中，那么后面的问题便可以从前面的阶段推导出来

2. 无后效性

无后效性有两层含义，我们之前学过回溯算法，我们知道回溯一般采用的是递归的思路，这个还记得吧，但是我们一定不要用脑子去思考每一步递归之后的结果，只需要考虑当前阶段的状态值就可以了，这是无后效性的第一层含义，第二层含义指的是，当我们确定的首次递归的状态了，那么就不会因为不断的递归而改变状态。

3. 重复子问题

如果用之前专栏中回溯算法的思想解释就是，不同的决策，在某个阶段，状态相同。

实例剖析

假设我们有一个n*n的矩阵w[n][n]，矩阵存储的都是正整数，棋子的起始位置在左上角，结束的问题在右下角，我们把矩阵内的数字当做路径的长度，每次移动一个单位，问左上角移动到右下角的最短路径是多少？

首先我们看看，这是否符合之前所说的一个模型？

我们从(0,0)走到(n-1,n-1)，总共要走2*(n-1),也就对应着2*(n-1)个阶段。每一个阶段都有向右走或者向下走两种策略，每一个阶段都是一个状态。

我们将状态定义为min_dist(i,j)，其中i表示行，j表示列。min_dist表达式的值表示从(0,0)到(i,j)的最短路径长度。所以，这个问题是一个多阶段决策最优解问题，符合dp模型

然后再看看是否符合三个特征：

1. 最优子结构：

我们将从(0,0)走到(i,j)的最小路径定义为min_dist(i,j).因为我们只能往右或者往下移动，所以我们可能会从(i-1,j)或者(i,j-1)到达(i,j)，也就是说min_dist(i,j)可以通过min_dist(i-1,j)或者min_dist(i,j-1)两个状态推出来，所以符合最优子结构。
min_dist(i,j) = w[i][j] + min(min_dist(i,j-1),min_dist(i-1,j))

2. 无后效性：

如果我们想要走到(i,j)这个位置，可以通过(i-1,j)或者(i,j-1)两种方式移动过来，也就是说，我们需要计算(i,j)位置对应的这个状态，只需要关心(i-1,j)或者(i,j-1)对应的状态即可，不需要关心具体的移动轨迹，因为只要前一个位置状态确定了，是不会被后面的决策所影响的，所以满足无后效性。

3. 重复子问题：

首先我们发现，确实可以用不同的路径走到相同的方格而且路径还是相同的。

解题思路

解决动态规划问题，我们一般采用两种思路：分别是状态转移表法和状态转移方程法。

1. 状态转移表法

一般情况下，使用动态规划的解决的问题，都可以用回溯的办法暴力破解，毕竟二者的区别就在于，动态规划重在存档和读档，而回溯则代表穷举。
只要存在重复子问题，第一种办法，可以使用“备忘录”避免重复子问题而消耗性能，从执行效率上讲，和动态规划没有什么区别，而第二种办法，就是我们说的状态转移表法，也就是dp思想来解决。

下面来主要介绍一下状态转移表法的思路：

首先我们需要画出一个二维的状态表，可以理解为二维数组，每个状态包括三个数值，行，列，数组值，从前往后，根据递推关系，填充状态表中的每个状态，然后将递推填表的过程，翻译成代码，就可以了。

当然，我上面介绍的仅仅是二维数组+一个状态值，但是如果是多个状态，就会很复杂，对应的状态将会变成三维甚至更高维，那么这种办法就不合适了

我们暂且先不说高维，先只说二维的情况，我们该如何使用这种方法，解决矩阵最短路径的问题？

思路：
<1> 先探究一下是否存在重复子问题，首先画出递归树，在递归树中，一个状态(也就是一个树叶)包含三个节点(i：行，j：列，dist：从起点到(i,j)的路径长度)，然后排除掉(i,j)相同但是dist长的节点，被排除的就不继续递推了。
<2>尝试使用动态规划的思想，我们画出状态表：


<3>书写代码，当我们知道的建表的过程，就可以来使用代码来实现出来了，我们将上面的过程实现成代码是这样的：

2. 状态转移方程法

状态转移方程的思路类似于递归算法，某个问题如何通过子问题来递归求解，通过不断的回溯获取到最优子结构，然后利用最优子结构写出递归公式，也就是我们所谓的状态转移方程，获取到方程后，我们可以使用递归+备忘录和迭代递推两种方法解决。

类似于刚才上面距离过的：
min_dist(i,j) = w[i][j] + min(min_dist(i,j-1),min_dist(i-1,j))

这里强调一下，状态转移方程是解决动态规划的关键，如果能写出方程，转化成代码也就简单多了。

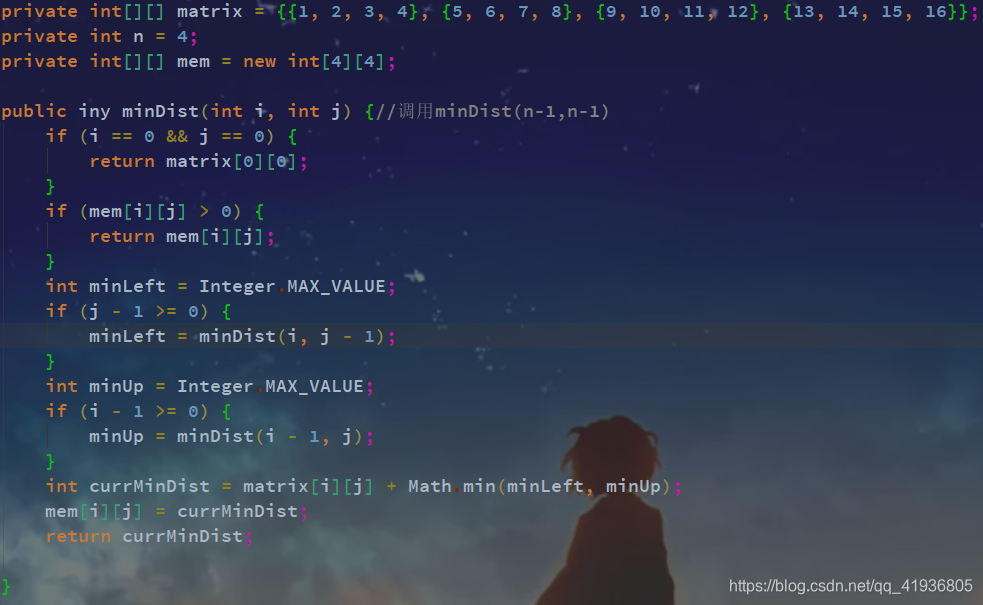
接下来我先用递归+备忘录的方法将上面的状态转移方程翻译成代码。

算法比较

接下来侧重于说一下贪心，分治，回溯，动态规划四种算法的区别与联系。

从思想上说，贪心，回溯，动态规划更侧重于解决多阶段最优解问题，分治算法虽然也是为了计算出最优解，但是往往没有多阶段模型。

回溯算法可以解决基本所有的最优解问题，因为算法本质就是穷举，但是由于时间复杂度太高，所以更侧重于去解决小数据的问题。

尽管动态规划算法比回溯更加高效，但是动态规划算法必须满足以下三点：最优子结构，无后效性和重复子问题。动态规划算法和分治算法最明显的区别就是，分治算法要求所有的计算都不能有重复情况，而动态规划却要求一定要有重复子问题。

贪心算法是动态规划算法中特殊的情况，因为贪心算法总是去获取局部最优，这和动态规划是不同的，局部最优不代表整体最优，所以存在一定局限性。