线性回归-----标准方程法实现线性回归方程

标准方程法推导

对于标准方程法，我们得到其损失函数如下（因为损失函数为二次函数，所以图像上只有一个坑，不可能出现多个极小值）：

将其展开为矩阵形式（这里矩阵中的$w$就是损失函数中的$\theta$，表示模型的参数，每一个$x$表示一个特征（$x_0表示偏置)$），$y$表示训练集的真实值）：

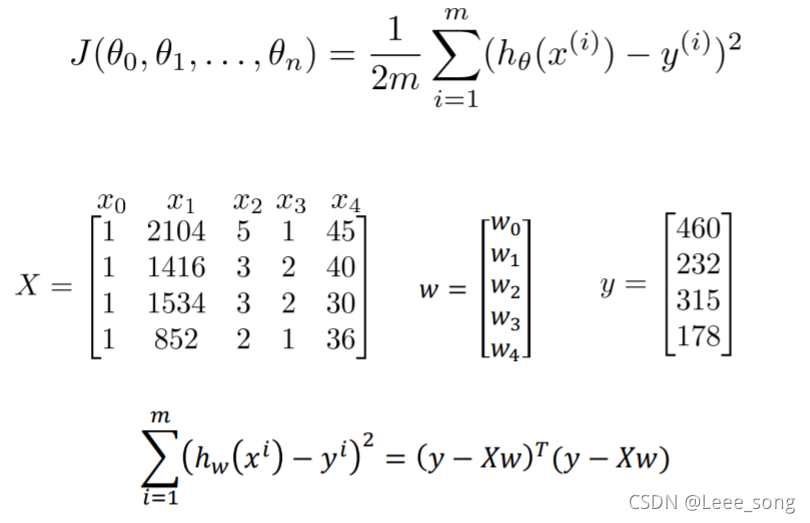
对矩阵进行求导：

梯度下降法和标准方程法的比较：

用python实现标准方程法

部分data.csv数据:

import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt

# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
# 去第0列为x_data，但是把x_data变成二维的
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]

# 给样本添加偏置项，将x_data添加一列1
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)


# 重点:标准方程法求解回归参数
def weights(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T*xMat # 矩阵乘法
    # 计算矩阵的值,如果值为0，说明该矩阵没有逆矩阵
    if np.linalg.det(xTx) == 0.0:
        print("This matrix cannot do inverse")
        return
    # xTx.I为xTx的逆矩阵
    ws = xTx.I*xMat.T*yMat
    return ws

# 调用标准方程法函数
ws = weights(X_data,y_data)

# 画图，取值从20取到80
x_test = np.array([[20],[80]])
y_test = ws[0] + x_test*ws[1]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_test, y_test, 'r')
plt.show()

说明：sklearn中的线性回归就是标准方程法实现的

用sklearn实现一元线性回归

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

data=np.genfromtxt("D:\gzu_ml\资料\程序\回归\data.csv",delimiter=",")

x_data=data[:,0,np.newaxis]
y_data=data[:,1,np.newaxis]
# 创建模型
model=LinearRegression()
# 训练模型
model.fit(x_data,y_data)

plt.plot(x_data,y_data,'b.')
plt.plot(x_data,model.predict(x_data),'r')
plt.show()

用sklearn实现二元线性回归

from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
from numpy import genfromtxt
import mpl_toolkits.mplot3d as Axes3D

data=np.genfromtxt("D:\gzu_ml\资料\程序\回归\Delivery.csv",delimiter=",")
# 切分数据
# 将前面两列作为x_data
x_data=data[:,:-1]
# 最后一列作为y_data
y_data=data[:,-1]

# 创建模型
model=linear_model.LinearRegression()
# 训练模型
model.fit(x_data,y_data)


ax = plt.figure().add_subplot(111, projection = '3d')

ax.scatter(x_data[:,0], x_data[:,1], y_data, c = 'r', marker = 'o', s = 100) #绘制真实值  

x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
# intercept表示训练得到的截距，coef_表示训练得到的系数
z = model.intercept_+x0*model.coef_[0]+x1*model.coef_[1]
# 绘制二维平面
ax.plot_surface(x0, x1, z)
#设置坐标轴  
ax.set_xlabel('Miles')  
ax.set_ylabel('Num of Deliveries')  
ax.set_zlabel('Time')  
  
#显示图像  
plt.show()