后缀数组 学习笔记

后缀数组 学习笔记

果然我学过的东西都忘了。。。

Reference

以下博客写得相当好！

浅谈后缀数组算法——blackfrog 的博客

后缀数组详解——自为风月马前卒

后缀数组 (SA)——OI Wiki

一些定义

对于一个字符串 $S$, $|S|$ 表示它的长度。$S[l..r]$ 表示从 $l$ 截取到 $r$ 的子串。用“后缀 $i$” 或 “$\mathrm{s}\mathrm{u}(i)$” 表示字符串从 $i$ 开始的后缀，即 $S[i..|S|]$。

PART 1 后缀数组初见

主要介绍倍增法。算法思想请查阅以上三篇博客。本篇文章重在算法实现。

P3809 【模板】后缀排序

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
//char In[1 << 20], *ss = In, *tt = In;
//#define getchar() (ss == tt && (tt = (ss = In) + fread(In, 1, 1 << 20, stdin), ss == tt) ? EOF : *ss++)
ll read() {
	ll x = 0, f = 1; char ch = getchar();
	for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;
	for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + int(ch - '0');
	return x * f;
}
const int MAXN = 1e6 + 5;
int n;
char s[MAXN];
int sa[MAXN], rk[MAXN], x[MAXN], y[MAXN << 1], c[MAXN];
void SuffixSort() {
	int m = 'z' + 1;//max Sigma
	for(int i = 1; i <= n; i++) c[x[i] = s[i]]++;
	for(int i = 2; i <= m; i++) c[i] += c[i-1];
	for(int i = n; i >= 1; i--) sa[c[x[i]]--] = i;
	for(int k = 1; k <= n; k <<= 1) {
		int num = 0;
		for(int i = n - k + 1; i <= n; i++) y[++num] = i;
		for(int i = 1; i <= n; i++) if(sa[i] > k) y[++num] = sa[i] - k;

		for(int i = 1; i <= m; i++) c[i] = 0;
		for(int i = 1; i <= n; i++) c[x[i]]++;
		for(int i = 2; i <= m; i++) c[i] += c[i-1];
		for(int i = n; i >= 1; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;

		for(int i = 1; i <= n; i++) swap(x[i], y[i]);
		x[sa[1]] = 1; num = 1;
		for(int i = 2; i <= n; i++)
			x[sa[i]] = (y[sa[i]] == y[sa[i-1]] && y[sa[i] + k] == y[sa[i-1] + k]) ? num : ++num;
		if(num == n) break;
		m = num;
	}
	for(int i = 1; i <= n; i++) rk[sa[i]] = i;
}
	
int main() {
	scanf("%s", s+1); n = strlen(s+1);
	SuffixSort();
	for(int i = 1; i <= n; i++) printf("%d ", sa[i]);
	printf("\n");
	return 0;
}

---

看不懂？没关系，让我们结合代码仔细分析。

int n;
char s[MAXN];
int sa[MAXN], rk[MAXN], x[MAXN], y[MAXN << 1], c[MAXN];

$n$ 是字符串长度，$s$ 存储字符串。

$sa[i]$ 表示排名为 $i$ 的后缀的 位置，而 $rk[i]$ 表示位置为 $i$ 的后缀的 排名。我们发现这一对类似于反函数的关系。即 $sa[rk[i]]=i,rk[sa[i]]=i$。请精确地记住这个定义！

$x[i]$,$y[i]$ 分别表示基数排序的的第一、第二关键字。话虽如此，它在代码中的意思经常变化，请结合下文注释食用。另外，这里 $y[i]$ 要开两倍空间，原因你会在后文看到。

---

接下来，进入 SuffixSort() 函数内部看看。

int m = 'z' + 1;//max Sigma

$m$ 代表字符集。

for(int i = 1; i <= n; i++) c[x[i] = s[i]]++;
for(int i = 2; i <= m; i++) c[i] += c[i-1];
for(int i = n; i >= 1; i--) sa[c[x[i]]--] = i;

这是一次基数排序了。它以 $i$ 为第二关键字，$x[i]=s[i]$ 为第一关键字。在这里 $c$ 数组是用于桶排的辅助数组。我们不仅得到了一开始的第一关键字，还得到了 初始化的 $sa$ 数组，表示 按 $(s[i],i)$ 二元组排序后第 $i$ 名的位置。

for(int k = 1; k <= n; k <<= 1)

开始倍增，$k$ 为倍增长度。

int num = 0;
for(int i = n - k + 1; i <= n; i++) y[++num] = i;
for(int i = 1; i <= n; i++) if(sa[i] > k) y[++num] = sa[i] - k;

这里 $num$ 只是相当于一个数组下标的推进，就类似于动态开点里的 $tot$ 一样的功能。

重点： 这里 $y[i]$ 数组的含义：表示第二关键字为第 $i$ 名的后缀的位置。于是 $x[y[i]]$ 可以表示这个后缀的第一关键字。

于是这里就很好理解了。位于 $i\in [n-k+1,n]$ 的后缀，它第二关键字 $i+k$ 已经超过了字符串的范围，所以第二关键字肯定是最先的。

而对于前面的那些 $i\in [1,n-k]$ 的后缀，它的第二关键字一定是一定是位于 $1+k,n$的字符串。于是我按照字符串的排名（即 $sa$ 数组的顺序）寻找那些位置 $\ge k$ 的字符串，那么它的位置 $-k$ 就是其对应的第一关键字了。

for(int i = 1; i <= m; i++) c[i] = 0;
for(int i = 1; i <= n; i++) c[x[i]]++;
for(int i = 2; i <= m; i++) c[i] += c[i-1];
for(int i = n; i >= 1; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;

标准化的桶排，根据 $x[i],y[i]$ 求出新的字符串的排名，手动模拟一下就知道了。

for(int i = 1; i <= n; i++) swap(x[i], y[i]);

重点： 在这里 $x[i],y[i]$ 的含义发生了变化。接下来要计算 新的第一关键字$x[i]$，于是把 原来的第一关键字 赋值到 $y[i]$ 避免被覆盖。

x[sa[1]] = 1; num = 1;
for(int i = 2; i <= n; i++)
	x[sa[i]] = (y[sa[i]] == y[sa[i-1]] && y[sa[i] + k] == y[sa[i-1] + k]) ? num : ++num;
if(num == n) break;
m = num;

这里开始计算 $x$ 数组了。此处 $num$ 的含义是 不同的第一关键字的种类数。按照后缀排名进行计算，如果这一位 原来的第一关键字 和 原来第二关键字 都与之前一位相同，则认为在新的第一关键字中这两位仍然相同，赋予相同的第一关键字。

如果可以使每个后缀都区别开，就没必要倍增了。

从这里也可以知道 $y$ 数组为啥要开 2倍空间了。

PART 2 LCP的妙用

LCP（Longest Common Prefix），最长公共前缀，是后缀数组的好拍档，可以让后缀数组发挥更大的威力。

以下内容部分选自许智磊的集训队论文《后缀数组》。

何为最长公共前缀？两个字符串 $S$, $T$，我们定义它们的最长公共前缀$\mathrm{l}\mathrm{c}\mathrm{p}(S,T)$ 为最长的一个字符串 $X$，满足 $X$ 既是 $S$ 的前缀，又是 $T$ 的前缀。有时也称 $X$ 的长度为 $\mathrm{l}\mathrm{c}\mathrm{p}(S,T)$。定义 $\mathrm{L}\mathrm{C}\mathrm{P}(i,j)$ 表示一个字符串中 排名为 $i$ 的后缀 和 排名为 $j$ 的后缀 的 lcp。

LCP有以下显然的性质：

• $\mathrm{L}\mathrm{C}\mathrm{P}(i,j)=\mathrm{L}\mathrm{C}\mathrm{P}(j,i)$
• $\mathrm{L}\mathrm{C}\mathrm{P}(i,i)=|\mathrm{s}\mathrm{u}(\mathrm{s}\mathrm{a}(i))|=n-\mathrm{s}\mathrm{a}(i)+1$

以及几个常用的结论：

LCP Lemma

L C P ( i , k ) = min ⁡ { L C P ( i , j ) , L C P ( j , k ) } \mathrm{LCP}(i,k)=\min\{\mathrm{LCP}(i,j),\mathrm{LCP}(j,k)\} LCP(i,k)=min{LCP(i,j),LCP(j,k)}，其中 $1\le i\le j<k\le n$.

LCP Theorem

L C P ( i , j ) = min ⁡ { L C P ( k , k + 1 ) , i ≤ k < j } \mathrm{LCP}(i,j)=\min\{\mathrm{LCP}(k,k+1),i\le k < j\} LCP(i,j)=min{LCP(k,k+1),i≤k<j}

LCP Corllary

$\mathrm{L}\mathrm{C}\mathrm{P}(j,k)\ge \mathrm{L}\mathrm{C}\mathrm{P}(i,k),i\le j<k$

可以感性理解一下。

根据 LCP Theorm，如果我们要求任意的 LCP，只要求出所有的 相邻名次的 LCP，就可以转化为 RMQ 问题了。

于是我们再做以下定义：

$\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(i)=\mathrm{L}\mathrm{C}\mathrm{P}(i,i-1)$

其中 $\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(1)=0$。

我们有以下 重要 结论：

$\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(\mathrm{s}\mathrm{a}(\mathrm{i}))\ge \mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(\mathrm{s}\mathrm{a}(\mathrm{i}-1))-1$

这决定了我们可以线性地求 $\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}$ 数组了。

void Height() {
    for(int i = 1, k = 0; i <= n; i++) {
        if(k) k--;
        int j = sa[rk[i]-1];
        while(i+k <= n && j+k <= n && s[i+k] == s[j+k]) k++;
        ht[rk[i]] = k;
    }
}

PART 3 应用

（以下应用摘抄自各博客与罗穗骞的集训队论文《后缀数组——处理字符》）

1. 重复子串问题

可重叠的最长重复子串

我们要明白一点：根据 LCP Corllary ，相邻名次的后缀的 LCP 是比较长的。也就是说，我们要找最长的 LCP 应该在相邻名次中找。

重复子串一定是某两个后缀的公共前缀。所以我们应该找到最大的 LCP 。根据上面所说，我们应该找相邻名次后缀的 LCP 的最大值，即 height 数组的最大值。

不可重叠的最长重复子串

我们先二分这个最长重复子串的长度为 $k$ ，转化为判断性问题：是否存在两个长度为 $k$ 的子串相同且不重叠。

我们按照名次，把 height 数组分成若干组。保证：

1. 同一组间任意两个后缀的 LCP 大于等于 $k$ ，即 除去第一个元素外，其它的height都大于等于 $k$。
2. 任意两组之间任意两个后缀的 LCP 小于 $k$，表现为：每组的第一个元素的 height 小于 $k$。

以上两个转化可以通过 LCP Theorem 得到。

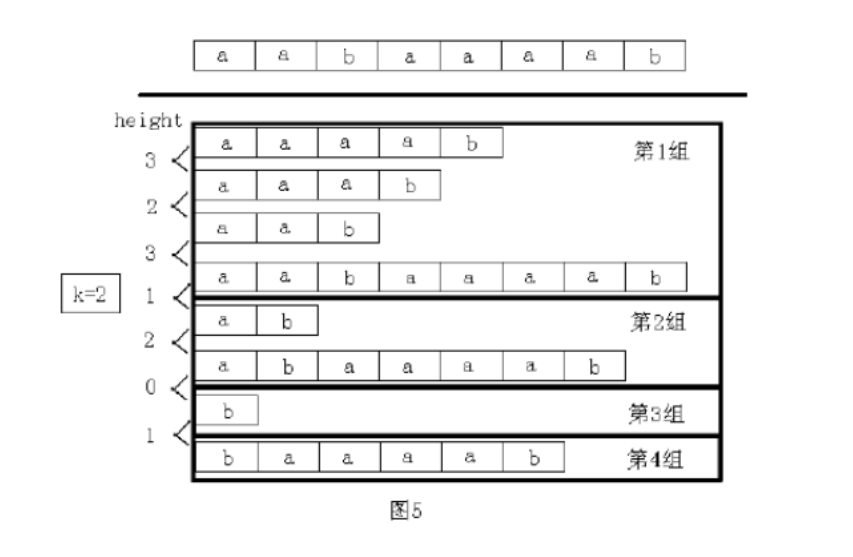
比如，这是 $k=2$ 的情况。（图片来自罗穗骞的集训队论文《后缀数组——处理字符》）

长度为 $k$ 的重复子串一定是于同一组中的两个后缀的公共前缀。怎么判断有没有不同的呢？只要求出每组的 sa 最大值和最小值，看看它们的差是否大于等于 $k$ 即可。

P2743 [USACO5.1]乐曲主题Musical Themes

可重叠的 $k$ 次最长重复子串

有两种思路：

1. 出现至少 $k$ 次，就要成为 $k$ 个后缀的公共前缀。于是转化为了求每 $k$ 个后缀的LCP最大值。我们只要求每相邻 $k-1$ 项的 $\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(i)$ 的最小值的最大值即可。可以用单调队列完成。时间复杂度 $O(n)$
2. 二分长度，按照 height 分组，看看有没有一组的长度大于等于 $k$。时间复杂度 $O(n\log n)$

P2852 [USACO06DEC]Milk Patterns G

2.子串个数问题

不同（非空）子串的数目

首先，一个长度为 $n$ 的子串都可以表述为 “一个后缀的前缀”。于是总共的子串数目为

$$\sum _{i=1}^n(n-i+1)=\frac{n(n+1)}{2}$$

在这基础上减去相同的子串数目。

考虑看看第 $i$ 名的后缀与第 $i-1$ 名的后缀之间重复计算了多少子串，显然就是 $\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(i)$。

所以最后的答案就是 $\frac{n(n+1)}{2}-\sum _{i=1}^n\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(i)$。

P2408 不同子串个数

SP705 SUBST1 - New Distinct Substrings