第 3 章 基础推荐算法

原文

相关性召回+点击率排序

推荐逻辑流程架构

根本任务: 匹配

匹配过程步骤:

1. 相关性召回, 对用户做360度全方位扫描, 尽量多的描述和覆盖用户可能感兴趣的高质量的物品;
2. 候选集融合, 重点关注多样性和相关性的均衡, 召回算法的优先级等问题;
3. 结果排序, 按照某一确定目标进行排序;
4. 业务干预

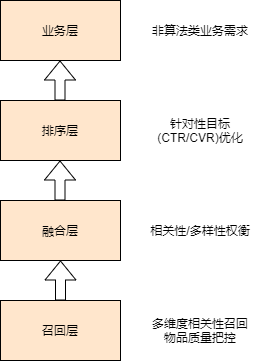
分层明确的逻辑架构, 有利于项目整体的并行化和效果调优的并行化;

召回算法的基本逻辑

匹配的常用计算路径:

1. 直接计算用户与物品的相关性;
2. 用户到物品的行为权重+物品与物品的相关性 => 用户与物品的相关性; (基于物品的协同过滤(Item-based CF)算法)
3. 用户与用户的相关性+用户到物品的行为权重 => 用户与物品的相关性; (基于用户的协同过滤(User-based CF)算法)
4. 用户与标签的相关性+标签与物品的相关性 => 用户与物品的相关性;

相关性, 由算法计算出的相关性, 认为是一种复杂相关性或静态相关性;

行为权重, 根据用户与物品之间产生的行为关系计算出的一种时效性较短的相关性, 认为是一种简单相关性或动态相关性;

常用的基础召回算法

用户与物品的相关性

基于矩阵分解的算法, 隐语义模型(Latent Factor Model, LFM), 将用户与物品之间的关系, 建模为 “用户到隐特征 + 隐特征到物品” 的链条, 然后通过求解隐特征信息来求解整个链条;

矩阵 $R$ 表示用户对物品行为的原始矩阵
$$R=\left\{\begin{array}{cccc}{r}_{1,1}& r_{1,2}& \cdots & r_{1,I}\\ r_{2,1}& r_{2,2}& \cdots & r_{2,I}\\ ⋮& ⋮& \ddots & ⋮\\ r_{U,1}& r_{U,2}& \cdots & r_{U,I}\end{array}\right\}$$
每一行表示一个用户, 每一列表示一个物品, 每个元素 $R_{u,i}$ 表示用户 $u$ 对物品 $i$ 的行为;

矩阵分解则是分解为:

$$\begin{gathered} R\approx X^T\times Y \\ X=\left\{\begin{array}{cccc}{x}_{1,1}& x_{1,2}& \cdots & x_{1,U}\\ x_{2,1}& x_{2,2}& \cdots & x_{2,U}\\ ⋮& ⋮& \ddots & ⋮\\ x_{K,1}& x_{K,2}& \cdots & x_{K,U}\end{array}\right\},Y=\left\{\begin{array}{cccc}{y}_{1,1}& y_{1,2}& \cdots & y_{1,I}\\ y_{2,1}& y_{2,2}& \cdots & y_{2,I}\\ ⋮& ⋮& \ddots & ⋮\\ y_{K,1}& y_{K,2}& \cdots & y_{K,I}\end{array}\right\} \end{gathered}$$

X 矩阵每一列表示一个用户, Y 矩阵每一列表示一个物品; 每一行均表示一个隐类别;

优点:

• 发现人工没有找出的类别;
• 更好适应数据变化; 根据用户的行为以及行为之间的关系找到隐类别, 时效性比较强;
• 将用户, 物品与隐类别之间的关系进行量化;

缺点: 隐特征缺乏直接的解释, 导致隐变量这个中间数据难易复用, 有效数据只有最终的用户和物品的数据;

LFM 思路: 先得到用户和物品的原始行为矩阵, 然后借助矩阵中有值(有行为)的元素来计算求解两个隐变量矩阵的值, 再用隐变量反过来求解缺失值元素的值, 从而得到推荐结果;

衍生出的相关模型: pLSA, LDA, 词嵌入, 句嵌入, 文档嵌入等;

LFM 求解 X, Y 转化为以下式子的优化问题(损失函数):
$$L=||R_{sample}-(X^T\times Y{)}_{sample}|{|}_F^2$$

$||M|{|}_F^2$ 是矩阵 $M$ 的 Frobenius 范数(F-范数)的平方, 表示矩阵中每个元素的平方和;
$$\begin{gathered} M=[a_{i,j}{]}_{m\times n} \\ ||M|{|}_F=\sqrt{\sum _{i,j}{a}_{i,j}^2} \end{gathered}$$
sample 下标代表矩阵中的样本集;

目标: 损失函数 L 取得最小值的 $x_{u,k}$, $y_{i,k}$:
$$L=\sum _{u,i\in sample}(r_{u,i}-\sum _k(x_{u,k}\times y_{i,k}){)}^2$$
单纯优化上式可能会出现过拟合现象, 所以加入正则化项:
$$L=\sum _{u,i\in sample}(r_{u,i}-\sum _k(x_{u,k}\times y_{i,k}){)}^2+\lambda (\sum x_{i,j}^2+\sum y_{i,j}^2)$$
其中, $\lambda$ 是正则化参数, 代表正则化力度;

求解方法有两种:

基于梯度下降的方法

随机梯度下降法(Stochastic Gradient Descent, SGD), 每次随机找一条训练样本, 求得其梯度, 然后将参数向梯度的反方向前进一步, 不断重复该过程, 求得一组结果稳定的参数值;

求两组参数 $x_{u,k}$ 和 $y_{i,k}$ 的偏导数:
$$\begin{gathered} \frac{\Delta L}{\Delta x_{u,k}}=-2(r_{u,i}-\sum (x_{u,k}\times y_{i,k}))y_{i,k}+2\lambda x_{u,k} \\ \frac{\Delta L}{\Delta y_{i,k}}=-2(r_{u,i}-\sum (x_{u,k}\times y_{i,k}))x_{u,k}+2\lambda y_{i,k} \end{gathered}$$
根据上面的梯度求得参数的前进方向:
$$\begin{gathered} x_{u,k}=x_{u,k}+\alpha ((r_{u,i}-\sum (x_{u,k}\times y_{i,k}))y_{i,k}-\lambda x_{u,k}) \\ {y}_{i,k}=y_{i,k}+\alpha ((r_{u,i}-\sum (x_{u,k}\times y_{i,k}))x_{u,k}-\lambda y_{i,k}) \end{gathered}$$
可以先将 $x_{u,k}$ 和 $y_{i,k}$ 随机初始化, 然后按上面公式不断迭代;

其中三个参数 $\lambda$(正则化系数) , $\alpha$(学习率) , $K$(隐特征) 都需要反复试验来确定最优值;

不基于梯度的交替最小二乘法

交替最小二乘法(ALS), 将两组参数交替保持一组固定不变, 来优化另外一组;

引入新变量: $c_{u,i}=1+\alpha r_{u,i}$

优化目标变更为:
$$L=\sum _{u,i}{c}_{u,i}(r_{u,i}-\sum (x_{u,k}\times y_{i,k}){)}^2+\lambda (\sum x_{i,j}^2+\sum y_{i,j}^2)$$

• 增加 $c_{u,i}$ 参数, 让每条样本都有不同的权重;
• 所有数据参与计算, 移除 sample 下标;

改写向量形式:
$$\begin{gathered} L=\sum _{u,i}{c}_{u,i}(r_{u,i}-x_u^T{y}_i{)}^2+\lambda (\sum _u||x_u|{|}^2+\sum _i||y_i|{|}^2) \\ L=\sum _{u=0,i=0}^{u=m,i=n}(c_{u,i}(r_{u,i}-x_u^T{y}_i{)}^2+\lambda (||x_u|{|}^2+||y_i|{|}^2)) \end{gathered}$$
通过微积分运算求得解析解:
$$\begin{gathered} x_u=(Y{C}^u{Y}^T+\lambda I{)}^{-1}Y{C}^u{R}_u \\ {y}_i=(X{C}^i{X}^T+\lambda I{)}^{-1}X{C}^i{R}_i \end{gathered}$$

物品与物品的相关性

从根本逻辑上划分算法:

• 基于行为的算法
  • 以余弦相似度为代表的相似度算法
  • 以 Apriori 与 FP-Growth 为代表的关联规则算法
• 基于内容的算法(后面介绍)

关联规则算法是对数据做了严格限制, 比如限制分析一次购物涉及的物品之间的关系, 计算出的数据相关性会更强, 由于使用了更少的数据而导致覆盖率较差;

相似度算法则是分析一段时间内购买行为数据, 相关性上有所牺牲, 但会有更好的多样性和覆盖率;

可以说相似度算法是一种广义的关联规则算法;

两个 N 维向量 X ($X=(x_1,x_2,\dots ,x_N{)}^T$)和 Y ($Y=(y_1,y_2,\dots ,y_N{)}^T$) 的余弦相似度:
$$consine(X,Y)=\frac{XY}{||X||||Y||}=\frac{{\sum }_{i=1}^N{X}_i{Y}_i}{\sqrt{{\sum }_{i=1}^N{X}_i^2}\sqrt{{\sum }_{i=1}^N{Y}_i^2}}$$
大数据稀疏情况下会造成两个层面的浪费:

• 物品对层面的浪费: 每个用户只会对少量物品产生行为;
• 点积层面的浪费: 少量用户同时对两个物品产生行为;

采用剪枝优化,

• 分子, 同时对物品 i 和物品 j 产生过行为的用户数, intersect(i, j);
• 分母, 物品 i 和物品 j 对应的向量长度, 即对物品 i 和物品 j 产生过行为的用户数, count(i), count(j);

优化后的计算流程:

1. 将用户到物品的行为原始数据转为物品到用户的倒排表;
2. 遍历倒排表得到所有的 intersect(i, j), 和所有的 count(i);
3. 使用 intersect(i,j) 和 count(i) 计算物品 i 和物品 j 之间的非零相似度;

用户与用户的相关性

同物品与物品的相关性计算方法, 将用户和物品位置互换即可;

一般网站, 用户数的量级要比物品数的量级大, 增加了用户之间相关性计算的复杂度; 所以要考虑业务特点和规模;

小结

以上介绍的方法都是基于用户行为的召回算法, 存在如下问题:

• 依赖用户行为, 扩展能力差(冷启动和时效性);
• 缺乏抽象, 知其然不知其所以然;
• 长尾挖掘能力差与滞后性, 直接依赖用户行为的算法, 也称基于记忆的算法, 对于新物品或长尾物品不利;

以下介绍基于用户画像(标签)的算法;

用户与标签的相关性

用户标签来源:

• 根据行为分析; => 行为权重+时间衰减;
• 根据行为分析+相关性; => 在1基础上再考虑标签的相关性;
• 不直接依赖用户行为, 用户本身属性; => 用户主动填写高权重, 算法推测低权重;

标签与物品的相关性

• 类别到物品, 常用方法是在召回热品, 新品或质量高的物品时, 加入一些品类下的重点物品; 过程中最好加入一些随机因素;
• 语义主题到物品, LDA, 通过贝叶斯公式得到每个主题下不同物品的概率 $P(do{c}_i|topic)=\frac{P(topic|do{c}_i)P(do{c}_i)}{{\sum }_{k}P(topic|do{c}_k)P(do{c}_k)}$
• 搜索词到物品;

将用户与物品的关系拆解为多个中间相关性的组合;

冷启动场景下的推荐

• 用户维度冷启动, 用户没有在系统中留下足够的行为;
• 物品维度冷启动, 新物品, 还没有足够多的用户对其产生行为;

解决方法: 基于内容的推荐算法, 或直接推荐畅销热品或新品;

冷启动时期推荐系统的责任:

1. 给出推荐结果;
2. 尽快探测用户的兴趣, 推荐种类丰富的物品, 增大命中用户兴趣的可能性;

解决冷启动问题, 在推荐系统中称为 Exploration & Exploitation 问题(EE问题), 即探索与利用问题;

参考文章

1. ALS交替最小二乘法推导