数据结构：树形结构之树及二叉树

人生就是一场修行，修的是自己的心。修行，就是扩大自己的心量。心量越大，自己的舞台就越大，能容的东西就越多。

什么是树形结构？

树形结构是元素之间具有分支，且具有层次关系的结构， 其分支、分展的特征类似
于自然界中的树木。

树的相关概念

树的定义

树是 N （N >= 0 ）个结点的有限集合，N = 0 时，称为空树，这是一种特殊情况。在任意一棵非空树中应满足：

1） 有且仅有一个特定的称为根的结点。

2）当 N > 1 时，其余结点可分为 m （ m > 0）个互不相交的有限集合T1 , T2 , T3 , … Tm ，其中每一个集合Ti本身又是一棵树，并且称为根结点的子树。

显然树的定义是递归的，是一种递归的数据结构。树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：

1）树的根结点没有前驱结点，除根结点之外的所有结点有且只有一个前驱结点。

2）树中所有结点可以有零个或多个后继结点。

二叉树的定义

二叉树 (Binany Tee)是n(n>=0)个结点的有限集合。当n=0时，称为空二叉树:当n>0时，该集合由个根结点及两棵互不相交的，被分别称为左子树和右子树的二又树组成。以前面定义的树为基础，二又树可以理解为是满足以下两个条件的树形结构。
1） 每个结点的度不大于2。
2）结点每棵子树的位置是明确区分左右的，不能随意改变。

由上述定义可以看出:二叉树中的每个结点只能有0、1 或2个孩子，而且孩子有左右之分，即使仅有一个孩子，也必须区分左右。位于左边的孩子(或子树)叫左孩子(左子树),位于右边的孩子(或子树)叫右孩子(右子树)。

二叉树的链式存储结构

二叉树的存储结构有顺序存储结构和链式存储结构，顺序存储是按照对满二叉树的节点连续编号的次序，将二叉树中编号为i的及节点放入数组的第i个分量中。

这种存储方式适合于满二叉树或完全二叉树，并且很容易计算出左右孩子或双亲的下标位置，但对于一般的二叉树来说，若二叉树的深度为k，则需要2^k个存储单元，特别是单支的二叉树，空间浪费极大。使用链式存储可动态分配内存空间。

C语言实现二叉树

#include <stdio.h>
#include <stdlib.h>
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>

#define ERROR 0
#define OK 1
#define TRUE 1
#define FALSE 0
#define NOTFOUND -1
#define biTreeDataType char

typedef struct biTree{

    struct biTree *LChild;
    biTreeDataType data;
    struct biTree *RChild;

}BiTree;

//二叉树的创建
void Create_BiTree(BiTree ** root){

    *root = (BiTree *) malloc(sizeof(BiTree));

    biTreeDataType elem;
    elem = getchar();

    if (elem == '#') {
        *root = NULL;
        return;
    } else {
        (*root)->data = elem;
        Create_BiTree(&((*root)->LChild));
        Create_BiTree(&((*root)->RChild));
    }
}

//数据访问
Visit(biTreeDataType data){

    printf("%c", data);
}

//先序遍历
void PrintPre_BiTree(BiTree *root) {

    if (root != NULL) {

        Visit(root->data);
        PrintPre_BiTree(root->LChild);
        PrintPre_BiTree(root->RChild);
    }
}

//中序遍历
void PrintMid_BiTree(BiTree *root){

    if (root != NULL) {

        PrintPre_BiTree(root->LChild);
        Visit(root->data);
        PrintPre_BiTree(root->RChild);
    }

}

//后序遍历
void PrintOrd_BiTree(BiTree *root){

    if (root != NULL) {

        PrintOrd_BiTree(root->LChild);
        PrintOrd_BiTree(root->RChild);
        Visit(root->data);
    }
}

//先序输出树的深度
void PrintPreAndGrade_BiTree(BiTree *root,int n) {

    if (root != NULL) {

        printf("%c %d\n", root->data, n);
        PrintPreAndGrade_BiTree(root->LChild,n+1);
        PrintPreAndGrade_BiTree(root->RChild,n+1);
    }
}

二分搜索树

二分搜索树( Binary Search Tree,BST),又称为二叉查找树，是一种高效的数据结构。它是满足以下性质的特殊二叉树。
二叉排序树或者是一棵空树，或者是具有如下特性的二叉树:
1）若它的左子树不空，则左子树上所有结点的值均小于根结点的值;
2）若它的右子树不空，则右子树上所有结点的值均大于根结点的值;
3）它的左、右子树也都分别是二叉排序树。
显然，这是一个递归定义，首先要保证结点的值之间具有可比性，另外，关键字之间不允许有重复出现。

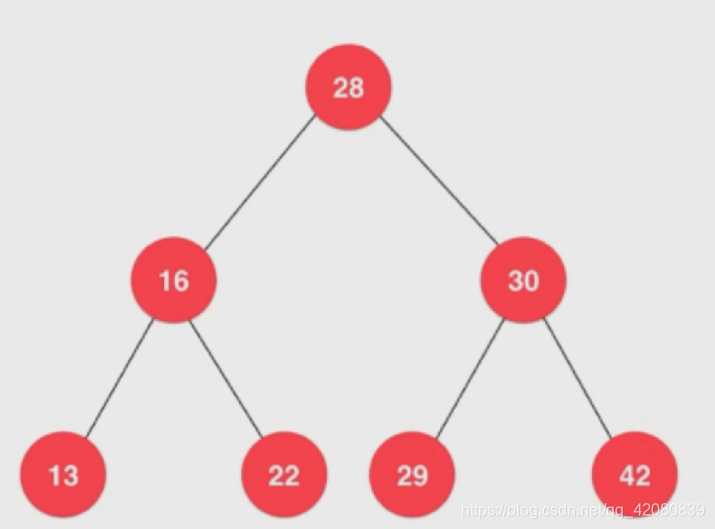
向二分搜索树中插入元素

插入一个元素事实上和查找十分相似，只不过是查找这个元素插入的位置，通过递归的方式，我们可以先找到插入的位置，然后将元素插入，最后返回插入完成后节点的根节点，这样逐层返回根节点。

	/**
     * 向二分搜索树中插入元素
     *
     * @param elem
     */
    public void add(T elem) {
        root = add(root, elem);
        size++;
    }

    private Node add(Node parent, T e) {

        if (parent == null) {
            return new Node(e);
        }

        if (e.compareTo(parent.data) > 0) { //忽略重复元素
            parent.right = add(parent.right, e);
        } else if (e.compareTo(parent.data) < 0) {
            parent.left = add(parent.left, e);
        }

        return parent;
    }

删除二分搜索树中的元素

删除元素相对复杂一些，删除一个元素会出现以下三种删除情况：

1. 待删除的节点是叶子结点
2. 待删除的节点只有左子树或只有右子树
3. 待删除节点既有左子树又有右子树
   虽然在删除的时候会有以上三种删除情况，但事实上其实只有两种，因为待删除节点是叶子节点可以看成是只有左子树或只有右子树的情况,因为空树也是二分搜索树。

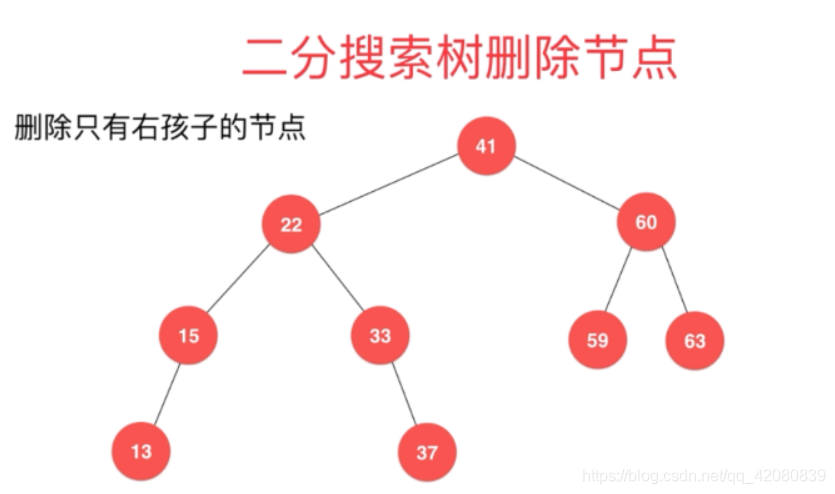
相信从上面几张图中发现，其实只有左子树或只有右子树的删除是很简单的：

• 如果只有左子树 ，那么就将删除结点的左子树的根节点去替换待删除节点的位置
• 如果只有右子树 ，那么就将删除结点的右子树的根节点去替换待删除节点的位置

那么如何实现删除左右子树都存在的节点呢？下面介绍由Habbard提出的Habbard Deletion算法。

根据这个算法，要删除左右子树都存在的节点实质上是用待删除节点的后继节点去替换他的位置：


d元素的后继为59，根据二分搜索树的特点，d节点的后继其实解释d节点右子树中的最小值。
到此59所在的节点解释s节点的后继节点s，接下来需要将s节点替换d节点。

将s节点从待删除结点d右子树中删除

然后让s节点的左子树和右子树分别连接上d的左子树和右子树。

最后删除d节点，s作为新子树的根返回。

至此就完成了左右子树都存在的节点的删除。

Java实现二分搜索树

package cn.boom.tree;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class BiSearchTree<T extends Comparable<T>> {

    private Node root;
    private int size;


    private class Node {

        private T data;
        private Node left;
        private Node right;

        public Node() {
            this.data = null;
            this.left = null;
            this.right = null;
        }

        public Node(T data) {
            this.data = data;
            this.left = null;
            this.right = null;
        }
    }

    public BiSearchTree() {
        root = null;
        size = 0;
    }

    /**
     * 获取树中元素个数
     *
     * @return
     */
    public int getSize() {
        return size;
    }

    /**
     * 树是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 向二分搜索树中插入元素
     *
     * @param elem
     */
    public void add(T elem) {

        root = add(root, elem);
        size++;
    }

    private Node add(Node parent, T e) {

        if (parent == null) {
            return new Node(e);
        }

        if (e.compareTo(parent.data) > 0) { //忽略重复元素
            parent.right = add(parent.right, e);
        } else if (e.compareTo(parent.data) < 0) {
            parent.left = add(parent.left, e);
        }

        return parent;
    }

    /**
     * 元素e是否存在
     *
     * @param e
     * @return
     */
    public boolean contains(T e) {
        return contains(root, e);
    }

    private boolean contains(Node parent, T e) {

        if (parent != null) {

            if (e.compareTo(parent.data) == 0) {
                return true;
            } else if (e.compareTo(parent.data) > 0) {
                return contains(parent.right, e);
            } else if (e.compareTo(parent.data) < 0) {
                return contains(parent.left, e);
            }
        }
        return false;
    }

    private void visit(T elem) {
        System.out.print(elem + " ");
    }

    //先序递归遍历
    public void preOrder() {
        preOrder(root);
    }

    private void preOrder(Node parent) {

        if (parent != null) {

            visit(parent.data);
            preOrder(parent.left);
            preOrder(parent.right);
        }
    }

    //先序非递归遍历
    public void preOrderNR() {

        Stack<Node> stack = new Stack<Node>();
        stack.push(root);

        while (!stack.isEmpty()) {

            Node node = stack.pop();
            visit(node.data);

            if (node.right != null) {
                stack.push(node.right);
            }

            if (node.left != null) {
                stack.push(node.left);
            }
        }

    }

    //中序递归遍历
    public void inOrder() {

        inOrder(root);
    }

    private void inOrder(Node parent) {

        if (parent != null) {

            inOrder(parent.left);
            visit(parent.data);
            inOrder(parent.right);
        }
    }

    //后序递归遍历
    public void postOrder() {

        postOrder(root);
    }

    private void postOrder(Node parent) {

        if (parent != null) {

            postOrder(parent.left);
            postOrder(parent.right);
            visit(parent.data);
        }
    }

    //层次遍历
    public void levelOrder() {

        Queue<Node> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {

            Node node = queue.remove();
            visit(node.data);

            if (node.left != null) {
                queue.add(node.left);
            }

            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }

    /**
     * 找最小值
     *
     * @return
     */
    public T minMum() {

        return minMum(root).data;
    }

    private Node minMum(Node parent) {

        if (parent == null) {
            throw new IllegalArgumentException(" BST is empty ！");
        }

        if (parent.left == null) {
            return parent;
        } else {
            return minMum(parent.left);
        }
    }


    /**
     * 找最大值
     *
     * @return
     */
    public T maxMum() {

        return maxMum(root).data;
    }

    private Node maxMum(Node parent) {

        if (parent == null) {
            throw new IllegalArgumentException(" BST is empty ！");
        }

        if (parent.right == null) {
            return parent;
        } else {
            return maxMum(parent.right);
        }
    }

    /**
     * 删除最小元素
     *
     * @return
     */
    public T removeMin() {

        T minElem = minMum();
        root = removeMin(root);
        return minElem;
    }

    /**
     * 返回删除结点后的根节点
     *
     * @param parent
     * @return
     */
    private Node removeMin(Node parent) {

        if (parent == null) {
            throw new IllegalArgumentException(" BST is empty ！");
        }

        if (parent.left == null) {

            Node rightNode = parent.right;
            parent.right = null;
            size--;
            return rightNode;

        } else {

            parent.left = removeMin(parent.left);
            return parent;
        }
    }

    /**
     * 删除最大元素
     *
     * @return
     */
    public T removeMax() {

        T elem = maxMum();
        root = removeMax(root);
        return elem;
    }

    /**
     * 递归删除最大元素，返回根节点
     *
     * @param parent
     * @return
     */
    private Node removeMax(Node parent) {

        if (parent == null) {
            throw new IllegalArgumentException(" BST is empty ！");
        }

        if (parent.right == null) {

            Node leftNode = parent.left;
            parent.left = null;
            size--;
            return leftNode;

        } else {

            parent.right = removeMax(parent.right);
            return parent;
        }
    }


    /**
     * 删除元素e
     *
     * @param e
     */
    public void remove(T e) {
        root = remove(root, e);
    }


    public Node remove(Node parent, T e) {

        if (parent == null) {
            return null;
        }

        if (e.compareTo(parent.data) > 0) {

            parent.right = remove(parent.right, e);
            return parent;
        } else if (e.compareTo(parent.data) < 0) {

            parent.left = remove(parent.left, e);
            return parent;
        } else {

            if (parent.left == null) {

                Node rightNode = parent.right;
                parent.right = null;
                size--;
                return rightNode;
            }

            if (parent.right == null) {

                Node leftNode = parent.left;
                parent.left = null;
                size--;
                return leftNode;
            }

            //左右子树均不为空
            //从右子树中得到比待删结点大的最小元素结点，并用此节点顶替删除结点
            Node replaceNode = minMum(parent.right);//removeMin中size--，因此不需要在维护size了

            replaceNode.right = removeMin(parent.right);
            replaceNode.left = parent.left;
            parent.left = parent.right = null;

            return replaceNode;
        }
    }
}

参考文献

[1]王曙燕.数据结构与算法:人民邮电出版社