马拉车算法主要用于解决字符串中最长回文串的问题,回文串是指正着读反着读都一样的字符串(例如:aba)。
在解决这种问题时我们会发现回文串主要分为两种,一种是长度为偶数的(例如abba),一种是奇数的(例如aba),他们有着不同的对称中心,所以得分别处理,马拉车算法的精髓之处就在于把两种字符串都同一处理了,他在字符串每个字符前后都加上一个字符串中没有的字符(例如加入“#”,那么字符串就会变为“#a#b#b#a#”或者是“#a#b#a#”),这样无论是偶数的还是奇数的都会变为奇数的,这样可以同一处理。
我们通过添加字符得到了新的字符串,接下来就对新的字符串求解其最大回文串长度。
算法的主要目的就是求出以字符串中每个字符为中心的回文串的最大长度(由于加入“#”的缘故,回文串都变成了奇数,所以肯定是以一个字符为中心的),将其存放在数组P[]中。以“babad”为例:

当得出P[i]时,计算原始回文串(去除“#”的回文串)的长度就很简单了,即为P[i]-1,推倒如下:
在以i点为中点的回文长度为(2P[i]-1),半径为P[i]。设在其中的“#”有x个,其他字符有y个,则:
x + y = 2P[i] - 1
由于在每个字符前后都有一个“#”,显而易见“#”要比其他的字符多一个,则:
x-y=1
解以上两个方程得:
y= P[i] - 1
知道了我们得目的那么接下来就开始遍历我们得到的新字符串,首先我们定义几个变量:
max 当前最大的回文串长度
r 当前遍历过的回文串中,右边界最大的那个回文串的右边界
l 当前遍历过的回文串中,右边界最大的那个回文串的左边界
ix 当前遍历过的回文串中,右边界最大的那个回文串的中心
i 当前位置
在遍历过程中,会遇到的情况主要如下:
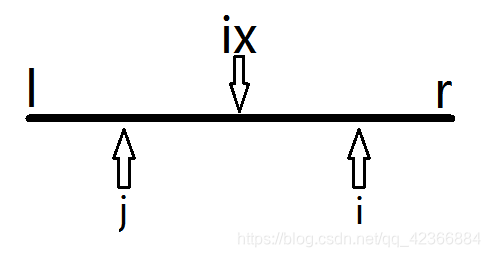 1.i点要小于r,这时由于[l,r]是关于ix对称的,所以在[l,r]的范围内,i与j(i关于ix的对称点)是一样的,这时对比 P[j] 和 r-i,如果P[j] 要小于r-i,则P[i] 也应该小于r-i,及i点处的回文在[l,r]的范围内,如果 P[j] 要大于r-i,则P[i] 要大于或者等于r-i,具体多大,可以暴力求解,可以先另P[i]=r-i,不断对比下一个是否等于关于i点对称的那一个。
1.i点要小于r,这时由于[l,r]是关于ix对称的,所以在[l,r]的范围内,i与j(i关于ix的对称点)是一样的,这时对比 P[j] 和 r-i,如果P[j] 要小于r-i,则P[i] 也应该小于r-i,及i点处的回文在[l,r]的范围内,如果 P[j] 要大于r-i,则P[i] 要大于或者等于r-i,具体多大,可以暴力求解,可以先另P[i]=r-i,不断对比下一个是否等于关于i点对称的那一个。
2.i点大于等于r,可以先另P[i]=1,接着暴力求解
做完上述工作后,还需对比i点处的右边界是否大于了原先的r,max是否小于了P[i]-1,做一些更新操作。
例子:
接下来我们用字符串“aba”做个简单的例子讲解
1.先将“aba”处理为“#a#b#a#”
2.初始化参数,ix=0,r=0,max=0,i=0
3.此时ix,r 都在0处,i此时也在0处,i不比r小则,则P[i]=1,对比i下一个和上一个,但i没上一个,则更新P[i]=1,右边界,ix不变。
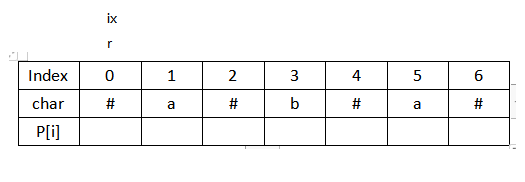
4.i开始移动,此时i大于r,令P[i]=1,暴力遍历,得出P[i]=2,接着更新右边界和ix,此时max为1
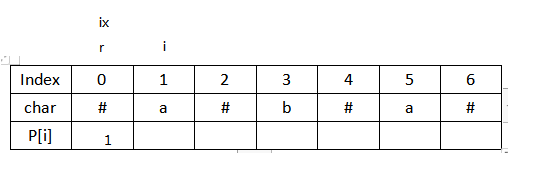
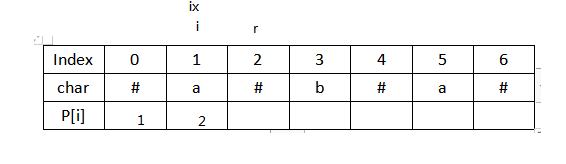
5.i移动至2处,不小于r,操作同上,得出p[2]=1,不用做更新
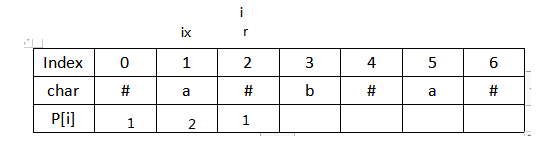
6.i移动到3,大于r,暴力求解,得P[3]=4,更新r,ix,max=3
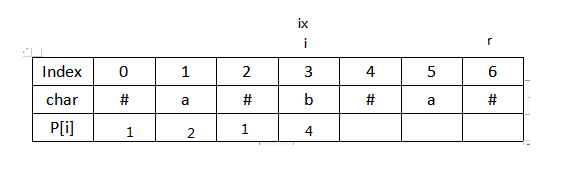
7.接着i到4,小于r,其关于ix的对称点P[j]=1,r-i=2, P[j]<r-i 则令P[4]=1,不做更新。
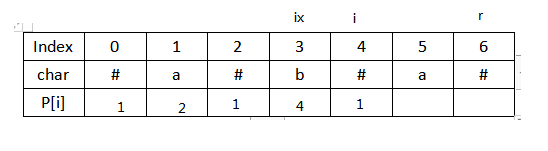
8.后面以此类推。
代码如下:

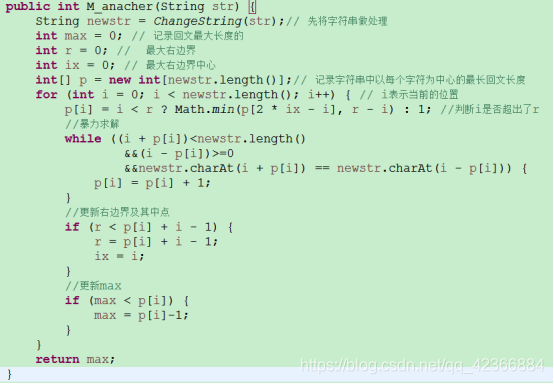





 马拉车算法是一种解决字符串中最长回文串问题的有效方法。它通过在原字符串前后添加特殊字符,使得所有回文串长度变为奇数,然后通过遍历新字符串,计算以每个字符为中心的回文串长度,存储在数组P[]中。算法核心在于利用已知回文串信息,减少重复计算。以字符串'aba'为例,解释了马拉车算法的步骤和更新过程,并给出了简单的代码实现。
马拉车算法是一种解决字符串中最长回文串问题的有效方法。它通过在原字符串前后添加特殊字符,使得所有回文串长度变为奇数,然后通过遍历新字符串,计算以每个字符为中心的回文串长度,存储在数组P[]中。算法核心在于利用已知回文串信息,减少重复计算。以字符串'aba'为例,解释了马拉车算法的步骤和更新过程,并给出了简单的代码实现。
















 275
275

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








