leetcode 232. 用栈实现队列思考分析

最新推荐文章于 2022-10-07 20:59:43 发布

原创最新推荐文章于 2022-10-07 20:59:43 发布 · 285 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#队列 #栈 #数据结构

leetcode刷题笔记同时被 2 个专栏收录

83 篇文章

订阅专栏

栈与队列

5 篇文章

订阅专栏

本文介绍了一种利用两个栈实现队列的方法，通过将数据压入输入栈，并在需要时将输入栈的数据转移到输出栈以模拟队列的先进先出特性。此方案支持push、pop、peek和empty等队列基本操作。

题目

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列的支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：
你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
进阶：
你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。
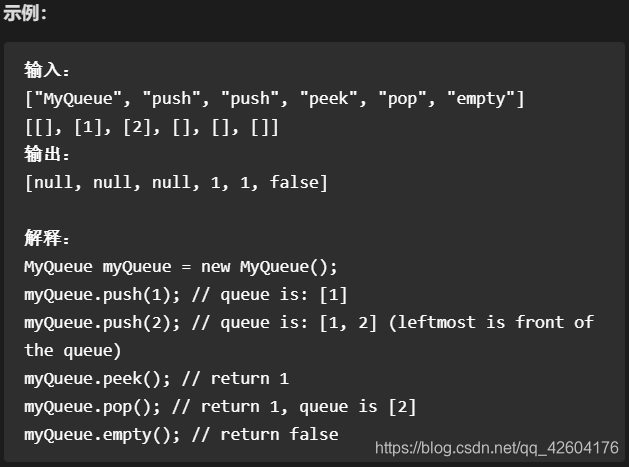
在这里插入图片描述

参考别人思路，使用双栈思想

push数据：把数据放进输入栈

pop数据:

输出栈如果为空，就把输入栈数据全部导入，再从输出栈弹出数据

如果输出栈不为空，则直接从输出栈弹出数据就可以了。

如何判断队列为空：如果输入栈和输出栈都为空，则说明模拟的队列为空。

代码

class MyQueue {
public:
    stack<int> stIn;
    stack<int> stOut;
    /** Initialize your data structure here. */
    MyQueue() {

    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        stIn.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        //如果输出栈为空
        if(stOut.empty())
        {
            //就把数据全部导入
            while(!stIn.empty())
            {
                stOut.push(stIn.top());
                stIn.pop();
            }
        }
        //从输出栈弹出数据
        int result =stOut.top();
        stOut.pop();
        return result;
    }
    
    /** Get the front element. */
    int peek() {
        //直接使用已有pop函数
        int res = this->pop();
        //因为pop()函数弹出了元素res，所以还得再添加回去
        stOut.push(res);
        return res;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return stIn.empty() && stOut.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */